转载自:https://blog.csdn.net/daaikuaichuan/article/details/80586408
一、迪杰斯特拉(Dijkstra)算法
1、定义描述
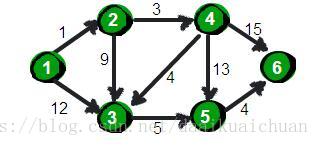
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法的时间复杂度为O(N^2)。例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径:
2、算法思想
设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
3、算法步骤
- 将所有的顶点分为两部分:已知最短路程的顶点集合P和未知最短路径的顶点集合Q。最开始,已知最短路径的顶点集合P中只有源点一个顶点。我们这里用一个book[ i ]数组来记录哪些点在集合P中。例如对于某个顶点i,如果book[ i ]为1则表示这个顶点在集合P中,如果book[ i ]为0则表示这个顶点在集合Q中。
- 设置源点s到自己的最短路径为0即dis=0。若存在源点有能直接到达的顶点i,则把dis[ i ]设为e[ s ][ i ]。同时把所有其它(源点不能直接到达的)顶点的最短路径为设为∞。
- 在集合Q的所有顶点中选择一个离源点s最近的顶点u(即dis[u]最小)加入到集合P。并考察所有以点u为起点的边,对每一条边进行松弛操作。例如存在一条从u到v的边,那么可以通过将边u->v添加到尾部来拓展一条从s到v的路径,这条路径的长度是dis[u]+e[u][v]。如果这个值比目前已知的dis[v]的值要小,我们可以用新值来替代当前dis[v]中的值。
- 重复第3步,如果集合Q为空,算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。
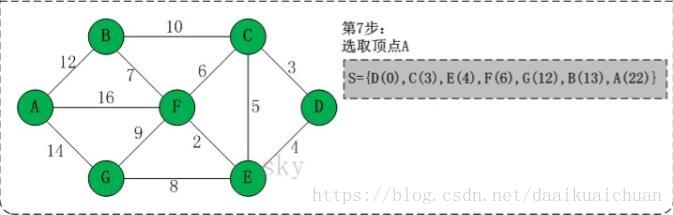
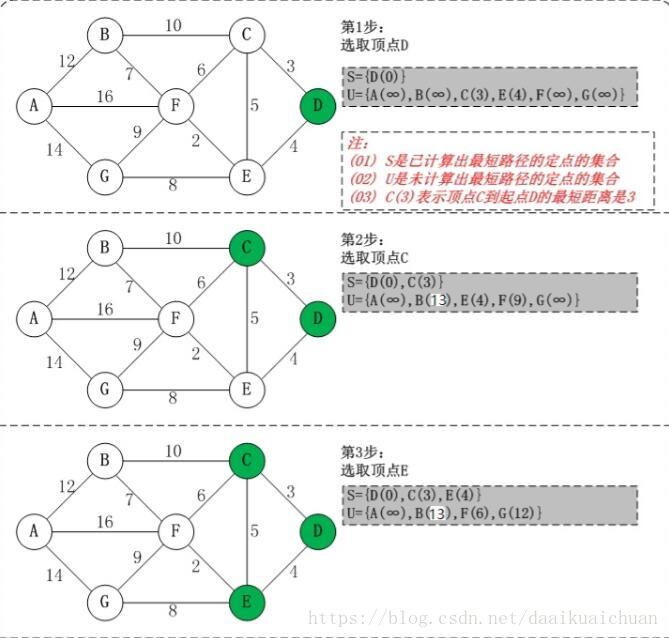
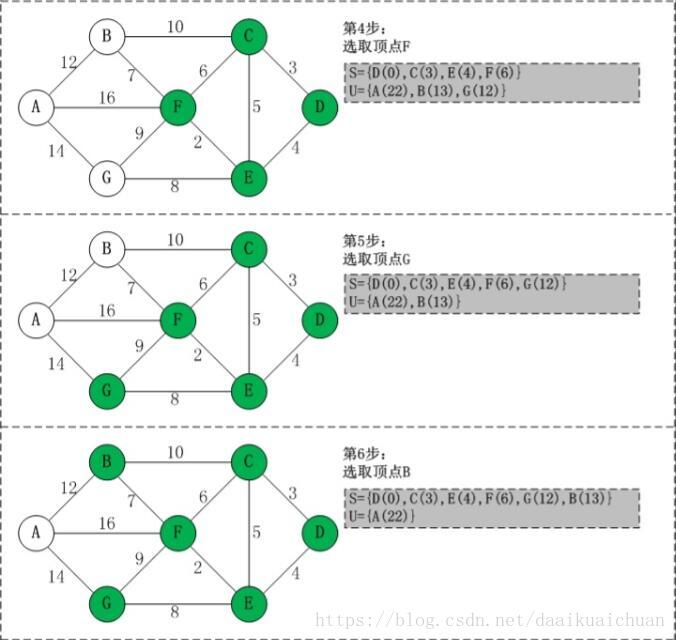
4、算法图解
二、弗洛伊德(Floyd)算法
1、定义描述
Floyd算法是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。Floyd算法的时间复杂度为O(N^3),空间复杂度为O(N^2)。
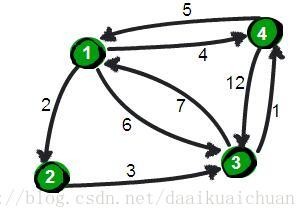
上图中有4个城市8条公路,公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程,也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。
2、算法思想
Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释。
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
3、算法步骤
- 从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
- 对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
三、Dijkstra算法和Floyd算法的demo:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int inf = 999999;//不连通的点之间的距离设为无穷大
long long int e[10000][10000];
int dis[10000];//最短距离数组
int book[10000];//记录下哪些点被选中
//计算单点到全部顶点的距离
int Dijkstra(int &n, int &m, int &s, vector<vector<int>> &data, int &t)
{
//初始化任意两点之间的距离数组
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (i == j)
e[i][j] = 0;
else
e[i][j] = inf;
}
}
//把权值加入到任意两点之间的距离数组中
for (int i = 1; i <= m; ++i)
{
e[data[i - 1][0]][data[i - 1][1]] = data[i - 1][2];
}
for (int i = 1; i <= n; ++i)
{
if (i != s)
{
dis[i] = e[s][i];//记录源点到其余所有点的最短路径
book[i] = 0;//记录哪些点被选取了
}
}
int u, min;
for (int i = 1; i <= n - 1; ++i)
{
min = inf;
for (int j = 1; j <= n; ++j)
{
if (book[j] == 0 && dis[j] < min)//找到源点离还没有被选取的点中的最近顶点
{
min = dis[j];
u = j;//记录下最近顶点的位置
}
}
book[u] = 1;
/*
*例如存在一条从u到v的边,那么可以通过将边u->v添加到尾部来拓展一条从源点到v的路径,
*这条路径的长度是dis[u]+e[u][v]。如果这个值比目前已知的dis[v]的值要小,
*我们可以用新值来替代当前dis[v]中的值。
*/
for (int v = 1; v <= n; ++v)
{
if (e[u][v] < inf)
{
if (dis[v] > dis[u] + e[u][v])
dis[v] = dis[u] + e[u][v];//松弛
}
}
}
return dis[t];
}
//计算两两顶点之间的最短路径
void Floyd(int &n, int &m, vector<vector<int>> &data)
{
//初始化任意两点之间的距离数组
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
if (i == j)
e[i][j] = 0;
else
e[i][j] = inf;
}
}
//把权值加入到任意两点之间的距离数组中
for (int i = 1; i <= m; ++i)
{
e[data[i - 1][0]][data[i - 1][1]] = data[i - 1][2];
}
/*
*最开始只允许经过1号顶点进行中转,接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点
*进行中转,求任意两点之间的最短路程。用一句话概括就是:从i号顶点到j号顶点只经过前k号点的最短路程。
*/
for (int k = 1; k <= n; ++k)
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
if (e[i][j] > e[i][k] + e[k][j])
e[i][j] = e[i][k] + e[k][j];
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
cout << e[i][j] << " ";
cout << endl;
}
}
int main(int argc, char const *argv[])
{
int n, m, s, t;
cin >> n >> m >> s >> t;//输入顶点数和边数,以及起止位置
vector<vector<int>> Path_Cost;
for (int i = 0; i < m; ++i)
{
vector<int> vec;
int x;
for (int j = 0; j < n; ++j)
{
cin >> x;
vec.push_back(x);
}
Path_Cost.push_back(vec);
}
cout << Dijkstra(n, m, s, Path_Cost, t) << endl;
Floyd(n, m, Path_Cost);
system("pause");
return 0;
}参考:http://blog.51cto.com/ahalei/1383613
https://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html