数学（三）信息熵、相对熵(KL散度)和交叉熵

『熵』这个词语听起来很高大上，如果搞明白含义就会发现它其实比较简单，但是如果不经常用的话，会时长忘记，因而写这篇文章是为了备忘。如果大家想弄清楚熵以及熵延伸出来的相对熵(KL散度)以及交叉熵的话，也可以参考下这篇博客。

关键字：信息熵，相对熵，KL散度，交叉熵

本篇博客首先会通过生活中的例子来讲解熵的由来，并且依次为基础介绍相对熵(KL散度)和交叉熵，因而本篇博客的主要内容如下：

• 信息熵
• 相对熵(KL散度)
• 交叉熵
• 总结

---

1. 信息熵

在一开始学信息论中的熵的时候，老师举了这样一个较为抽象的例子来辅助理解：假如一个事件有8种可能情况，且这8种可能情况发生的概率相同，都是1/8，那么这个事件最少可以通过几个二进制位来表示？如果一个事件有8种可能情况，但是现在已经知道了其中的1种情况发生的概率为1/2，剩余7种情况的概率为1/14，那么这时这个事件最少可以通过几个二进制位来表示？

为了能让学生更容易理解，老师举了一个生活中具体的例子：假如一个箱子里面有8种颜色的球( $c_1, c_2, c_3, c_4, c_5, c_6, c_7, c_8$)，每种颜色的球数量相同，那么老师从箱子里捞出一个球让学生猜，平均最少猜几次才能猜中球的颜色，当然每次猜测的内容是任意的。

首先想到的最蠢的方法是一个一个地问，比如第一次询问是否是 $c_1$，如果不是 $c_1$，则继续问 $c_2$…，那么这样下去平均会猜 $\frac{1+2+3+4+5+6+7+7}{8}=4.375$次才能猜到最终答案。而目前能想到的最快确定球颜色的方法是二分法，即第一次询问的内容为是否为 $c_1, c_2, c_3, c_4$其中的一个颜色，如果是的话，则继续问是否为 $c_1, c_2$的其中的一个颜色，如果是的话，最终再问一次是否为 $c_1$，就能找到答案，当然如果学生得到的答案是否定的话，则从询问内容的补集中找答案，询问的过程类似于二叉树的遍历，下图可以辅助理解。

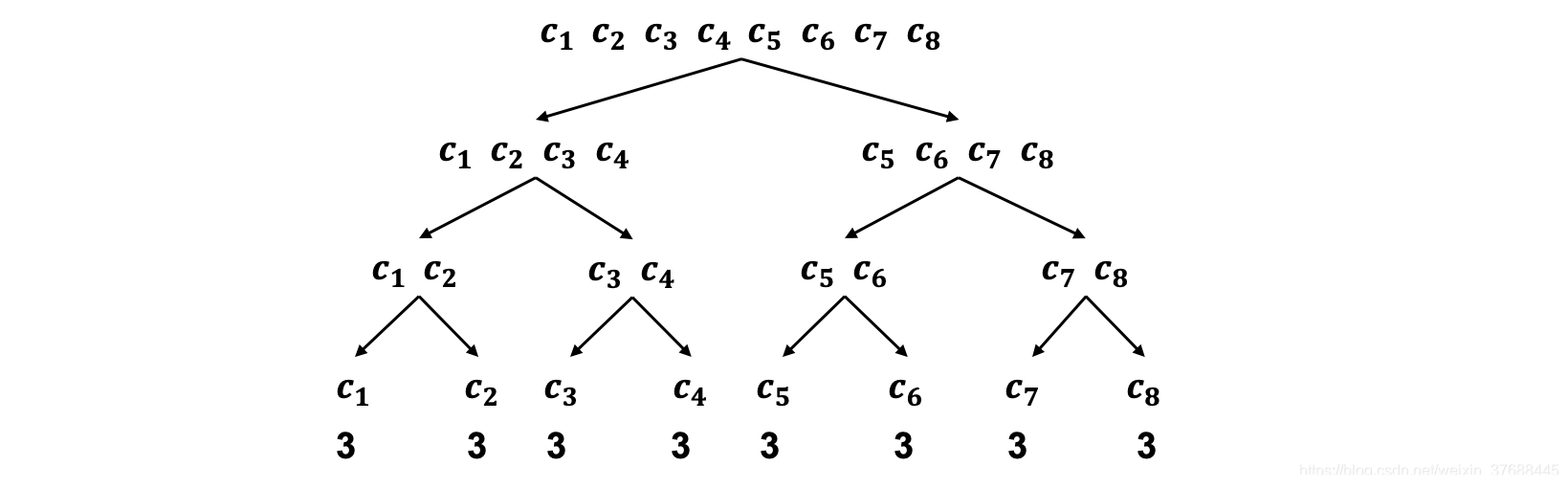
可以看到，每条路径所对应的猜的次数都是3，因而猜球的平均次数为：
$F_{mean}=\frac{1}{8}*3+\frac{1}{8}*3+\frac{1}{8}*3+\frac{1}{8}*3+\frac{1}{8}*3+\frac{1}{8}*3+\frac{1}{8}*3+\frac{1}{8}*3=3$

下面举另外一个例子，还是猜球游戏，如果学生被告知颜色为 $c_1$的球个数为整个箱子中球个数的1/2，其他颜色的球个数占比为1/14，那么这时需要按照占比的不同改变下二分法猜球的策略，询问的方式如下图所示，

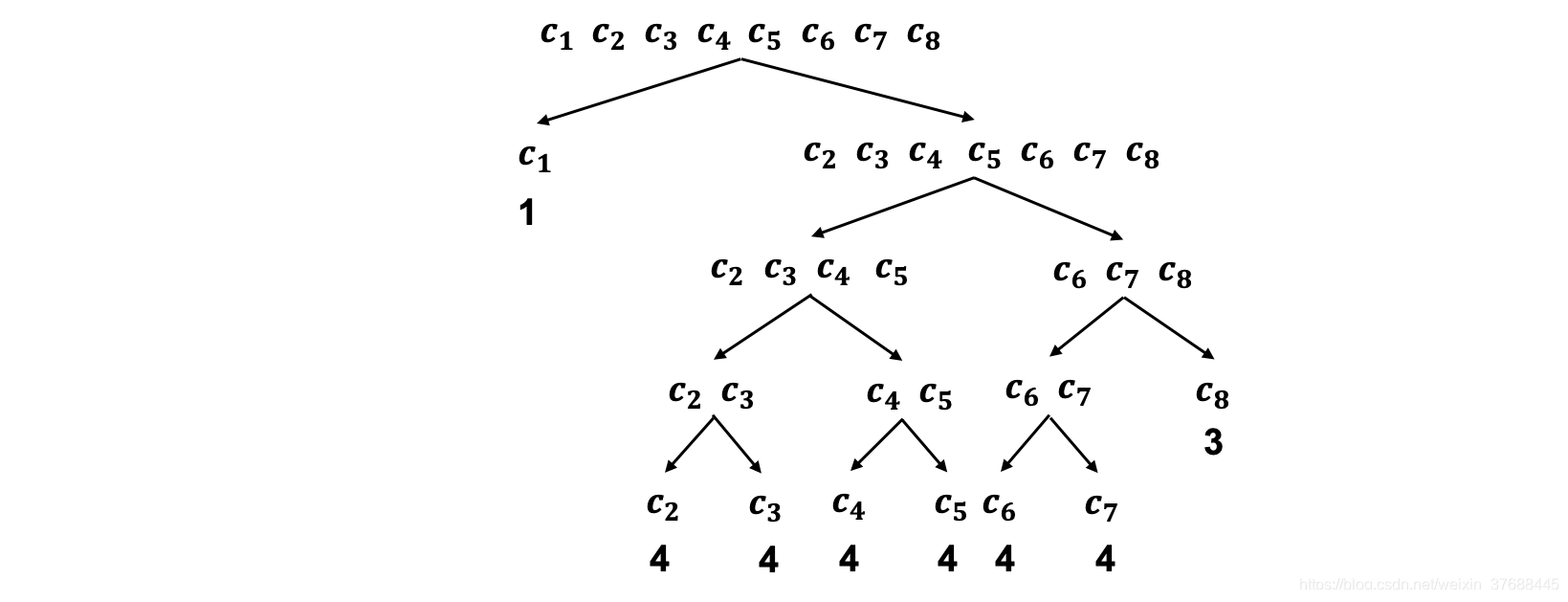
这种情况下猜球的平均次数为：
$F_{mean}=\frac{1}{2}*1+\frac{1}{14}*4+\frac{1}{14}*4+\frac{1}{14}*4+\frac{1}{14}*4+\frac{1}{14}*4+\frac{1}{14}*4+\frac{1}{14}*3\cong 2.83$

上述例子中以 $c_i$为叶子结点的路径长度即为二分法猜球的次数，具体到公式如下所示，其中向上取整是因为次数必须是一个整数，
$F_i = - \lceil log_2(p_i) \rceil$
平均猜球次数的公式如下所示，其实就是一个简单的加权平均，
$F_{mean}= - \sum_{i=1}^{M}p_i\lceil log_2(p_i) \rceil$

如果将次数不限制为整数，则可以将 $\lceil \rceil$去掉，去掉后就变为了大名鼎鼎的信息熵。
$F_{mean}= - \sum_{i=1}^{M}p_ilog_2(p_i)$

信息熵官方的解释是一个事件的不确定性，换到真实例子上来无非是猜球的平均次数，一个事件的不确定性越大，即猜球的平均次数就越多。

2. 相对熵

还是沿用上面的例子，上文一直都在说学生该如何猜球，这次来说说老师。现在老师知道这个箱子里球的分布为 $(\frac{1}{2}, \frac{1}{14},..., \frac{1}{14})$，但学生并不知道，而且老师没有透露给学生任何信息，这时老师让学生来捞出球的颜色，从而计算猜球的平均次数。

由于学生这次根本不知道任何信息，所以只能认为所有球的占比相同，都是1/8，因而这时询问的方式如下图所示，

这时猜球的平均次数为：
$F_{mean}=\frac{1}{2}*3+\frac{1}{14}*3+\frac{1}{14}*3+\frac{1}{14}*3+\frac{1}{14}*3+\frac{1}{14}*3+\frac{1}{14}*3+\frac{1}{14}*3 = 3$

可以看出，如果学生知道球的真实分布，猜球次数约为2.83次，而如果瞎猜的话，平均猜球次数为3次，这时这两次猜球的平均次数差值为3-2.83=0.17次，而转换为公式则有如下公式，其中 $q_i$代表的是学生猜测的颜色为 $c_i$的球的占比，
$\begin{aligned} F_{mean, sub}=- \sum_{i=1}^{M}q_i\lceil log_2(p_i) \rceil - (- \sum_{i=1}^{M}p_i\lceil log_2(p_i) \rceil)\\ =\sum_{i=1}^{M}p_i\lceil log_2(p_i) \rceil-\sum_{i=1}^{M}q_i\lceil log_2(p_i) \rceil \end{aligned}$

同样地，如果去掉 $\lceil \rceil$，公式就是我们日常所说的相对熵，即KL散度，该公式衡量的是数据的预测分布和真实分布的差异，即学生按照自己的意愿所导出的平均猜球次数和最少平均猜球次数之间的差异，而相对熵越小，代表预测分布和真实分布越接近，而对应到当前例子来说，就是学生估计的不同颜色球的占比和真实占比越接近。
$KL(P||Q)=\sum_{i=1}^{M}p_i log_2(p_i) -\sum_{i=1}^{M}q_i log_2(p_i)$

3. 交叉熵

还是沿用上面的例子，如果现在学生们只想知道按照自己估计的球的占比推导出的平均猜球次数，那这时相当于去掉KL散度的前半段，这就是所谓的交叉熵，
$CrossEntropy=-\sum_{i=1}^{M}q_i log_2(p_i)$

机器学习中很多分类任务都以交叉熵作为损失函数，而模型迭代的目标就是让交叉熵最小，对应到当前例子，则是学生平均猜球的次数最小，而学生猜球的次数越小，这说明学生估计的球的分布和球的真实分布越接近，这里隐藏着一个数学理论，即对于任意的 $q_i$，只有当所有的 $q_i=p_i$时， $-\sum_{i=1}^{M}q_i log_2(p_i)$最小，由于这不是本篇博客的重点，因而在这里省略。

4. 总结

本篇博客借鉴了一个通俗易懂的例子来对信息熵、相对熵和交叉熵进行介绍，希望对大家能够有所帮助。

参考

1. 知乎大神CyberRep的分享