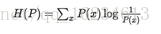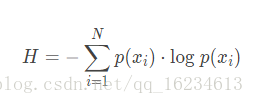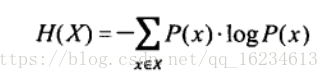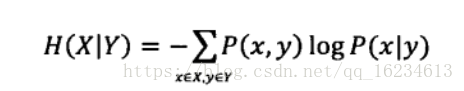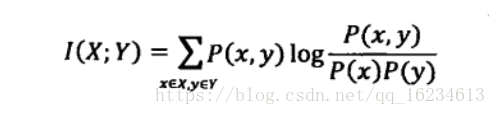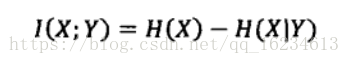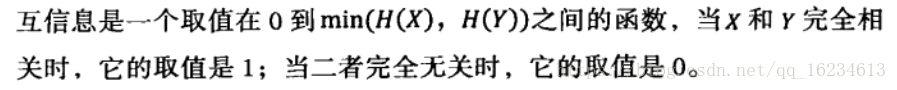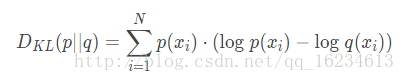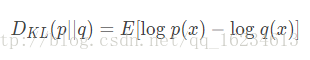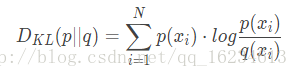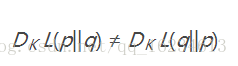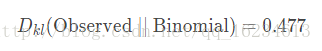当上述公式中概率相等时会推出,H刚好等于5比特。
自信息:
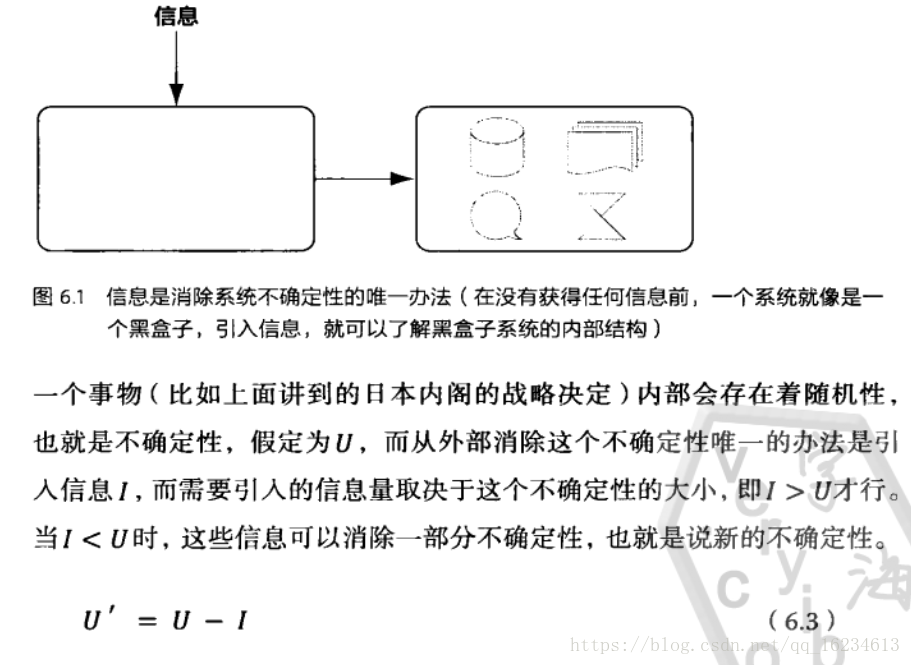
一条信息的信息量与该信息的不确定性有关。如果想要搞懂一件非常不清楚的事,就需要了解大量的信息,相反如果一件事我们已经了如指掌,那就不需要太多的信息来了解它。香农认为,信息可以消除我们对于事物认识上的不确定性,越不可能发生的事情一旦发生就可以消除较大的不确定性,所以应当含有较多的信息。由此,香农认为,应当用事件的发生概率确定该事件所含的信息量,概率越小的事件所含的信息量越大,而必然事件的信息量最小,指定为0。
熵:
想要知道一个分布的信息量,就要先确定一个描述信息量的量纲。 在信息论学科中,提出了熵的概念,记作 H。
对于一个随机变量,其概率分布所对应的熵表达如下:
或者是
变量的不确定性越大,熵也就越大,想要搞清楚它所需要的信息量也就越大。
上面两个公式其实类似,一个使用负号,一个使用除号。联合上面的自信息,可以知道,如果我们将自信息理解为一个事件出现的信息量,那么概率越大的事件所携带的信息量越少。那么负的概率和概率的倒数都可以表示信息量的多少。再使用期望信息量就能表示一个分布的信息量多少了。
如果我们使用 log2 作为底,熵可以被理解为:我们编码所有信息所需要的最小位数(minimum numbers of bits)。
信息的作用,条件熵:
为什么信息的引入会降低不确定性?
如果有x、y变量,根据x的分布可以计算出x的熵:
同时还知道x、y共同发生,以及在y条件下x的概率,则可以计算出在y条件下x的条件熵:
如果能够证明H(x)>=H(x|y),则表示不确定性减小了。如果引入的信息完全和x无关,此时就会出现等号情况。这也就证明了为什么二元模型比一元模型好。
互信息:
上文介绍到引入相关性信息从而减少不确定性。例如随机事件“下雨”和“空气湿度”有关。但我们需要有个度量来衡量这些相关性。香农提出使用“互信息”概念来量化度量。公式如下:
这个公式其实就是上文提到的x熵H(x)和H(x|y)的差异性。也就是由于信息引入带来的不确定性减少量。也就是在了解y的情况下对对消除x不确定性所提供的信息量。
在自然语言处理中,只要数据足够,很容易计算出两个随机变量x,y的概率和互信息。因此互信息被广泛应用于自然语言处理中。
KL散度:
相对熵(relative entropy)也叫KL散度(KL divergence)。用于度量两个概率分布的差异性,也就是相关性。KL散度计算的就是数据的原分布与近似分布的概率的对数差的期望值。与变量的互信息不同的是, 它用来衡量两个取值为正数的函数的相似性
设p和q是取值x的两个概率概率分布,则p对q的相对熵为:
记住:对于两个完全相同的函数,其相对熵为0;相对熵越大,两个函数的差异性越大,反之,相对熵越小,两个函数差异性越小;对于概率分布或者概率分布函数,如果取值大于0,相对熵可以衡量两个随机分布得差异性。
但注意KL散度不是距离度量(由于不满足对称性),且KL散度恒大于或等于0:
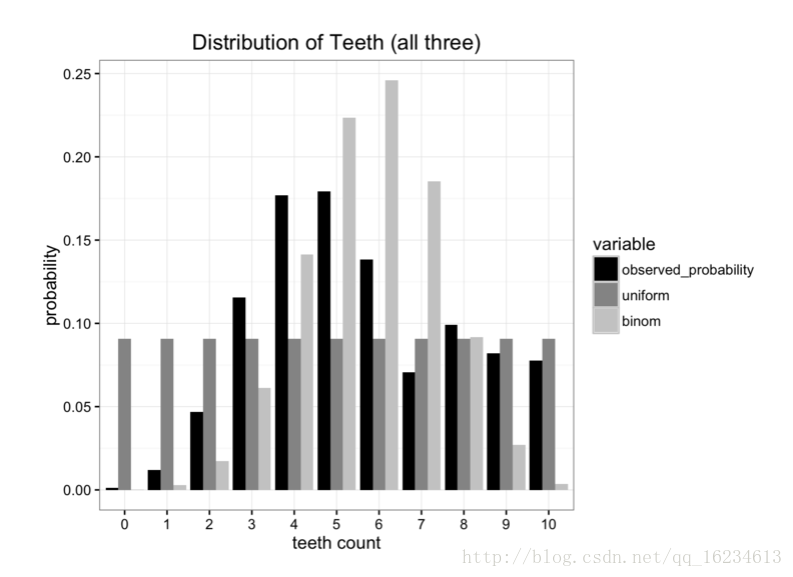
上图存在三个分布,一个是观察到的,另外两个属于我们预测的。那么预测哪一个更贴近原分布呢?就可以使用KL散度进行比较。
可以看到使用uniform分布表示原分布的信息损失量(0.338)要小于使用binomial分布(0.477)。所以优先选择uniform分布。
反向计算,可看到不满足对称性。
交叉熵:
应用:
1、衡量两随机分布间距离,如比较文本相似度。统计词频率,计算KL散度。
2、衡量选择的近似分布相比原分布损失多少信息。