简单理解信息量、散度、交叉熵

信息论

顾名思义，信息论是研究信息的一门学科，不过在这篇文章里，只讨论一些简单的概念。

信息量

这里的信息量和“这句话信息量很大啊”的信息量有些像，但还是有区别的。

信息论

顾名思义，信息论是研究信息的一门学科，不过在这篇文章里，只讨论一些简单的概念。

信息量

这里的信息量和“这句话信息量很大啊”的信息量有些像，但还是有区别的。

我们常说的信息量很大，基本上的意思是表达某句话或者某个场面（较少见）蕴含了很丰富的可解读信息，有着很大的脑补空间，可以让读者或者观众进行大限度的脑补、意淫、无限遐想。

然而信息论的基本想法是一个不太可能发生的事件发生了，要比一个非常可能的事件发生，有更多的信息。

比如我说：“人终究会死”，就没什么信息量，而“有个人跳楼没死”，信息就很丰富了。

当然了，在数学书上，总是要用公式来表示，这个定义是这样的，对于一个事件 $x$，它包含的信息量(自信息)为：
$I(x) = -lnP(x)$

这里使用了以 $e$为底的对数，单位是奈特(nats)，实际上，也可以使用以2为底的对数，它的单位是比特(bit)或香农。两者区别并不大，同一个信息只有常数倍的差距。

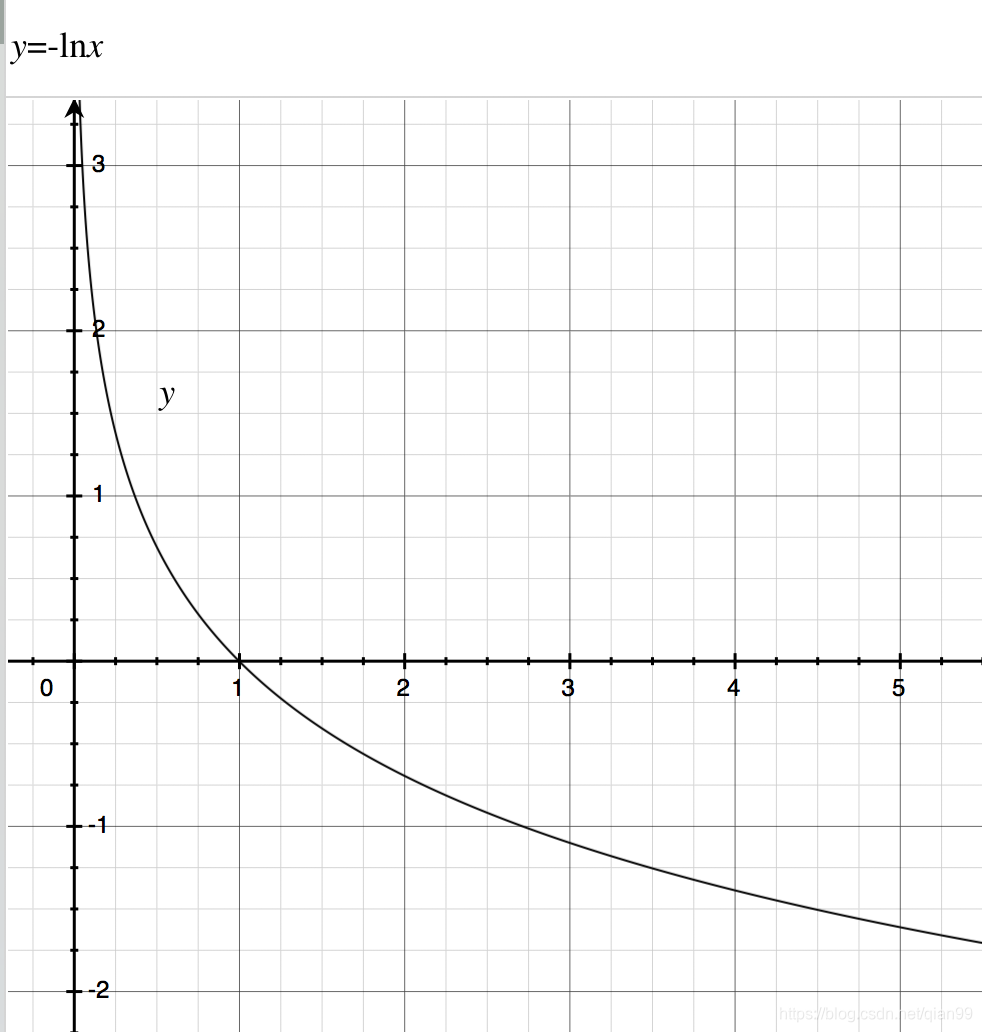
这里贴上 $-lnx$的函数，可以感受一下前面说的，当一个事件发生概率越大，信息量越小。

香农熵

上面说的自信息只针对单一事件，是单一事件信息量的量化，但是通常我们要对所有可能发生的事件做一个度量，也叫做香农熵。下面是公式：
$H(x) = E_{x \sim P}[I(x)] = -E_{x \sim P}[lnP(x)]$

香农熵其实就是所有可能发生的事件的信息量用它的概率的加权和。

我们把上面公式展开，思考一下概率分布与香农熵的关系：
$H(x) = - \sum_{x}P(x)lnP(x)$

这个东西我本来感觉应该有规律的，但是写了个代码看一下貌似没有，不过整体趋势应该是方差越小，整个值越大。而花书的说法是，越接近均匀分布，熵越高，越接近确定的分布，熵越低，接近确定分布和方差高不是一回事，花书上还给了个二值随机变量的例子：

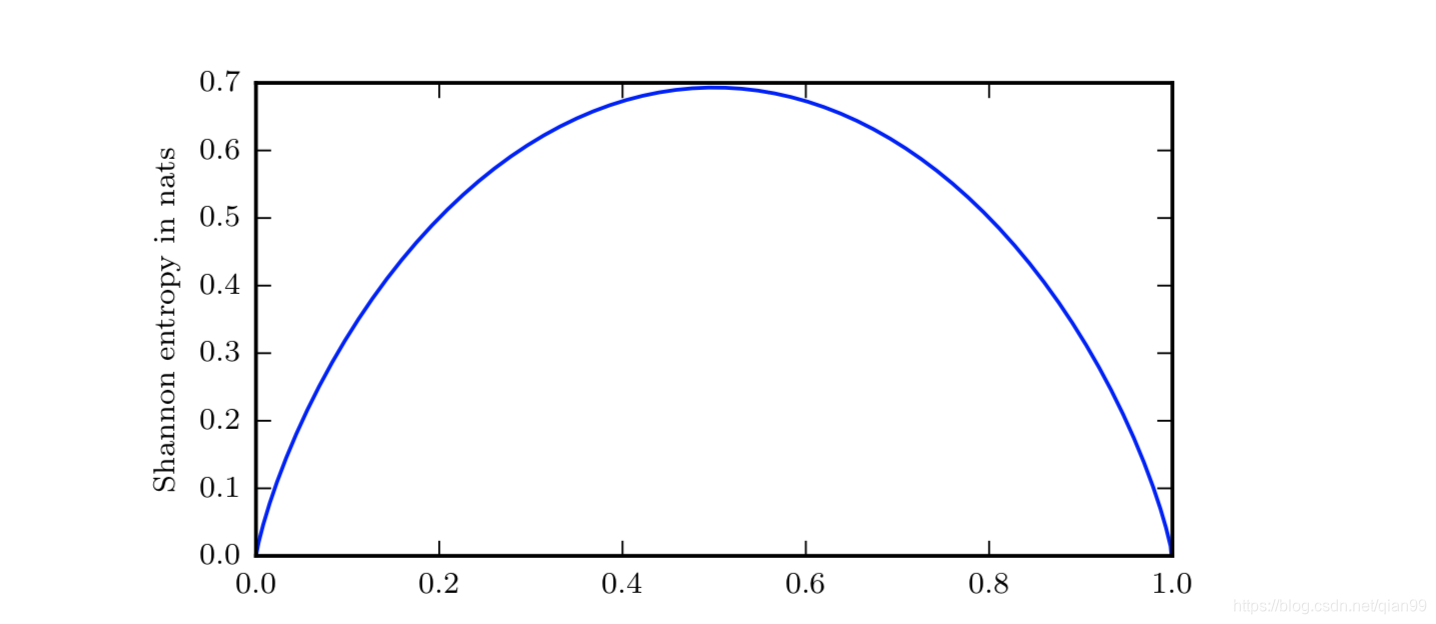
在上面的图中，横坐标是二值随机变量是1的概率，纵坐标是对应的香农熵。假设 $p$表示二值随机变量是1的概率，那么 $1-p$就是二值随机变量为0的概率。因此：
$H(x) = (p-1)log(1-p) - plogp$

• 当 $p\rightarrow 0$，随机变量几乎总是0，所以分布也是几乎确定的。
• 当 $p \rightarrow 1$，随机变量几乎总是1，分布也是几乎确定的，整个表达式还是趋近于0。

KL散度

上面写的都是针对同一个概率分布的，而想要衡量两个单独的概率分布之间的差异，就可以用到KL散度了。

假设有两个单独的概率分布 $P(x)$和 $Q(x)$，那么KL散度可以表示为：
$D_{KL}(P||Q) = E_{x \sim P}[log{\frac{P(x)}{Q(x)}}] = E_{x \sim P}[logP(x) - logQ(x)]$

花书上给KL散度一个解释：在离散型变量的情况下，KL 散度衡量的是，当我们使用一种被设计成能够使得概率分布 $Q$产生的消息的长度最小的编码，发送包含由概率分布 $P$产生的符号的消息时，所需要的额外信息量。

然而根本听不太懂啊。还是把公式展开分析一下吧：
$D_{KL}(P||Q) = E_{x \sim P}[log{\frac{P(x)}{Q(x)}}] = \sum_x{P(x)log{\frac{P(x)}{Q(x)}}}$

我们可以推出的一些信息是：

1. KL散度的值是大于等于0的，这个可以由吉布斯不等式推导出，这里不说。
2. KL散度等于0当且仅当 $P$和 $Q$在离散型变量的情况下是相同的分布，或者在连续型变量的情况下是"几乎处处"相同的。
3. KL散度是不对称的，即 $D_{KL}(P||Q) \neq D_{KL}(Q||P)$。

在前面也说了，KL散度是用来衡量两个分布的差距，但是上面提到了KL散度是不对称的，那么这两者作为一个指标有什么不同呢？

假设分布 $P$是固定的，我们要用一个分布 $Q$去近似它，这个时候KL散度就可以做为一个衡量的指标，我们的目标就是最小化KL散度。

接下来我们看第一种：
$D_{KL}(P||Q)= \sum_x{P(x)log{\frac{P(x)}{Q(x)}}}$

在这种情况下， $P$的分布是固定的嘛，我们需要考虑的是怎么调整 $Q$，在 $P$的值比较大的时候， $Q$越大，整个值就越大，而 $P$比较小的地方，由于左边乘了 $P$所以反而 $Q$的值影响没那么大。因此，如果我们使用 $D_{KL}(P||Q)$作为最小化的目标，那么 $Q$就应该在 $P$大的地方尽可能的大，在 $P$小的地方，在满足前面的条件下 $Q$也是要尽量大。

然后是第二种：
$D_{KL}(Q||P) = \sum_x{Q(x)log{\frac{P(x)}{Q(x)}}}$

思路和上面一样想让结果小，首先要保证在 $P$小的时候， $Q$也要小，在这个前提下， $P$大的地方， $Q$还是要小一些。

附上一张图：

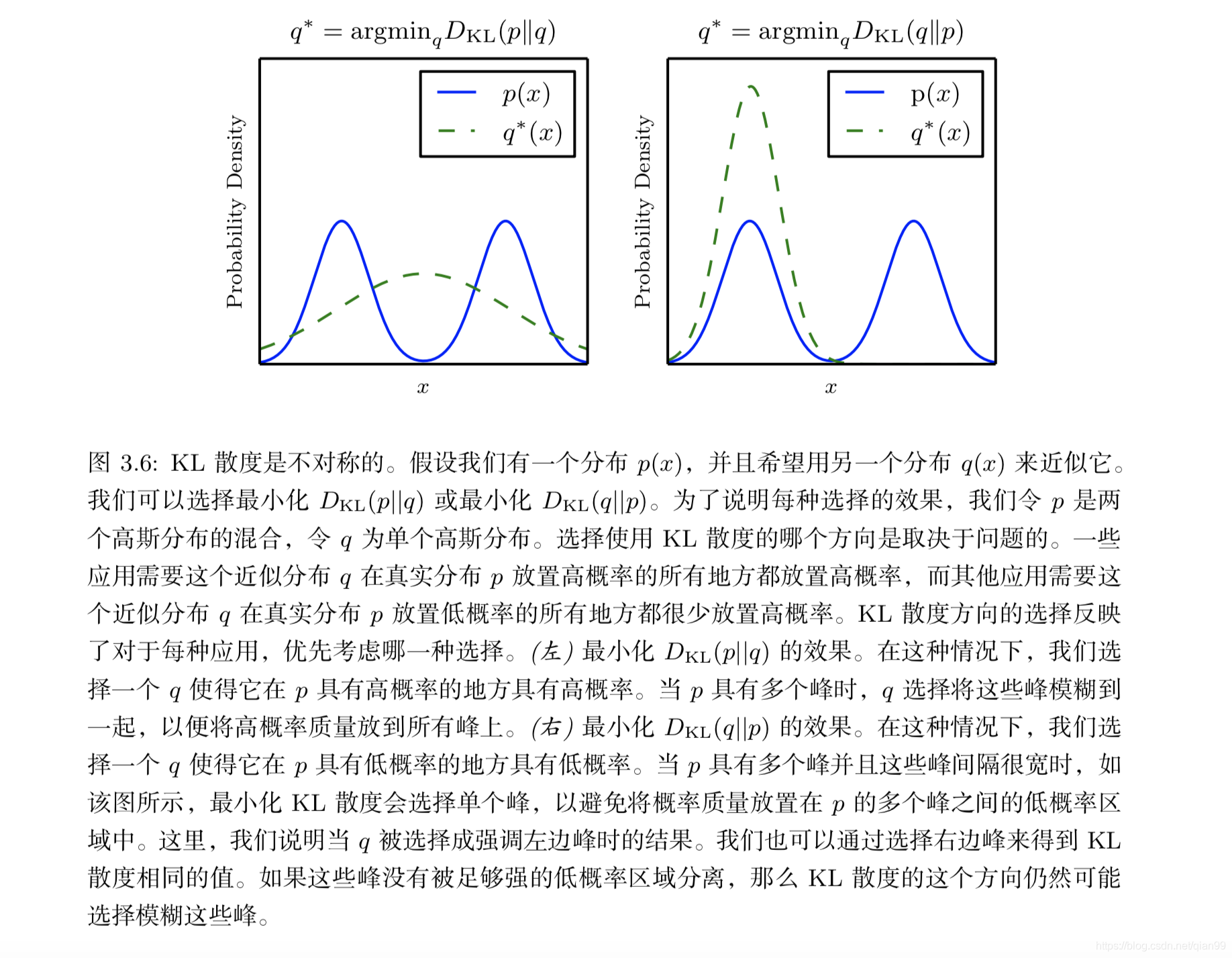## JS散度
JS散度是KL散度的一种变形，下面是公式：
$JS(P||Q) = \frac{1}{2}KL(P||\frac{P+Q}{2}) + \frac{1}{2}KL(Q||\frac{P+Q}{2})$

JS散度的值域是[0,1]。并且有一个好处，那就是对称性，从公式中就可以看出来 $JS(P||Q) = JS(Q||P)$

交叉熵

交叉熵其实和KL散度关系密切，先看一下公式：
$H(P,Q) = H(P) + D_{KL}(P||Q)$
$H(P, Q) = -E_{x \sim P}[log{Q(x)}]$
再回顾一下KL散度公式：
$D_{KL}(P||Q) = E_{x \sim P}[logP(x) - logQ(x)] = E_{x \sim P}[logP(x)] - E_{x \sim P}[logQ(x)]$
交叉熵其实就是KL散度去掉了左边那一项，如果我们固定 $P$优化的目标是 $Q$，那么优化KL散度和优化交叉熵的效果也是一样的，因为左边那一项是固定的。

最后一个问题，假定平常的分类任务中，训练数据可以用分布 $P$表示，为什么我们都是用 $H(P, Q)$而不是 $H(Q, P)$呢？我想，这可能是和它们优化的结果有关系吧，因为结果和KL散度的优化结果一样，我们可以参考上面KL散度那一节中的图，我的想法是， $H(P, Q)$可以覆盖 $P$的分布，而 $H(Q, P)$不能。

总结

上面的内容虽然不算难，但是在很多地方推导公式之类的都可能会用到，因此还是挺有用的。另外，如果有错误，欢迎大家指出。