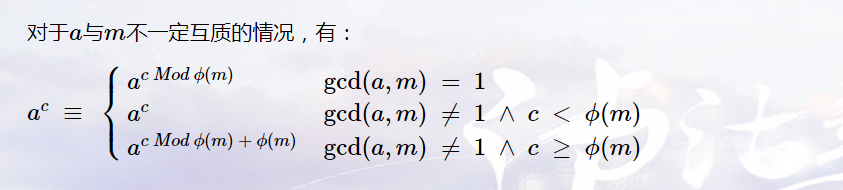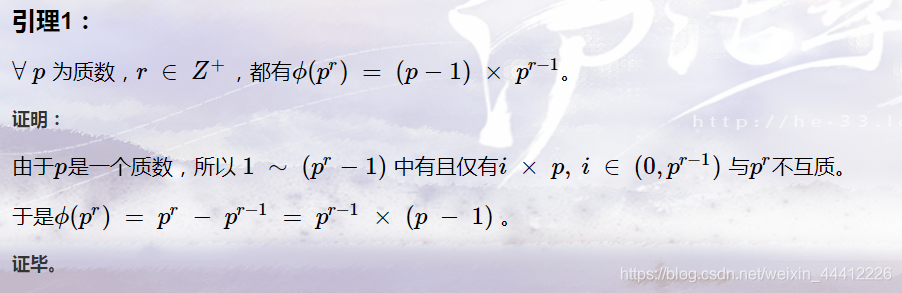欧拉定理及扩展证明转载

链接
$引理2的证明$
$就是p=ax,假定gcd(p,m)>1，那么p模m=r,gcd(r,m)>1 移项可得ax-mk=r 根据裴蜀定理ax-by=c的充要条件是gcd(a,b)|c，并且所有的解都能表示成ax-by=gcd(a,b)的解x',y'的c/gcd(a,b)倍 这样gcd(a,m)=1，所以x一定是r的倍数，这就矛盾了$
$总而言之，欧拉定理的证明是需要构造p_i=a*x_i$
$并且证明p_i两两模m不同（x_i同理）$
$pi模m与m互质$
$这样我们就可以推出pi模m共f(m)个，而x_i共m个且互相不同，所以就可以推出乘积模m相等$

扩展欧拉定理证明转载


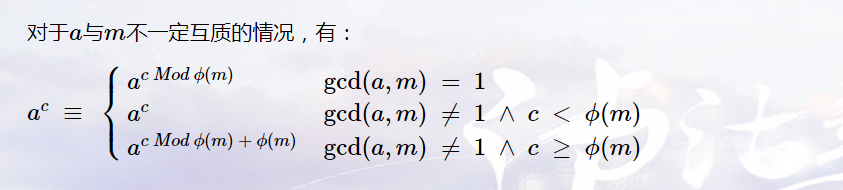
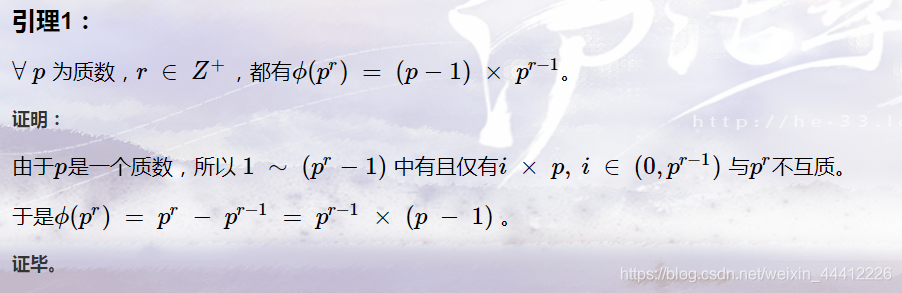
$该定理证明比较简单$
$证明过程中要用到积性函数的性质也就是证明任意组合质数$
$箭头所指的东西证明我也不太会，如果有人知道的话希望可以告诉我owo$