机器学习——正则化

1. 过拟合问题

首先，我们来看看过拟合问题的定义：

为了得到一致假设而使假设变得过度严格称为过拟合。

我们通过下面的图片直观理解什么是过拟合问题：

红色的叉叉代表我们的数据集。1. 假设我们用函数： $θ_0 + θ_1x$来拟合数据，得到的是一条简单的一次函数直线，很明显，这样的拟合过于简单，并不能反映数据的真实分布，我们称之为存在高偏差
2. 中间的图片：我们使用二次函数： $θ_0 + θ_1x + θ_2x^2$来拟合数据，现在非常好，拟合的程度可以反映数据的真实分布，我们称之为“Just Right”
3. 第三种情况：我们用一个高次函数 $θ_0 + θ_1x + θ_2x^2 + θ_3x^3 + θ_4x^4$来拟合数据，我们可以看到，曲线完全经过所给数据集，但是，这样曲曲折折的曲线却反而不能表达数据的真实分布了，这时我们称之为具有高方差，此时的情况就是过拟合

下面的例子中，最右边的也是过拟合问题的范例：

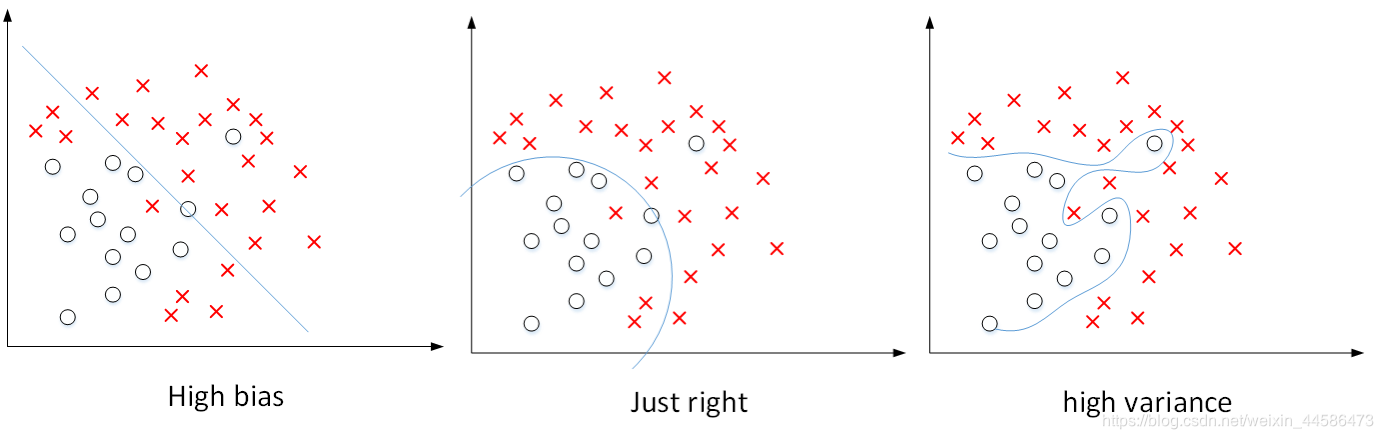
过拟合产生的问题就是模型不能很好地泛化到新样本中
正则化将会很好地解决过拟合问题，在后面几节的学习中，我们会详细学习它

2.正则化里面的代价函数

首先，让我们来看看博文第一张图片，看看正常的模型和过拟合模型的函数：
正常： $h_θ(x) = θ_0 + θ_1x + θ_2x^2$
过拟合： $h_θ(x) = θ_0 + θ_1x + θ_2x^2 + θ_3x^3 + θ_4x^4$
很显然，在本例中，过拟合问题就是由这些高次项系数 $θ_3, θ_4$产生的，因此，要缓解过拟合，我们就希望让 $θ_3, θ_4$尽量小，怎么做呢？

首先，这是我们本来需要最小化的代价函数： $J(θ) = \frac{1}{2m}\sum_{i = 1}^m(h_θ(x^{(i)}) - y^{(i)})^2$
现在，我们对它进行一些改动： $J(θ) = \frac{1}{2m}\sum_{i = 1}^m(h_θ(x^{(i)}) - y^{(i)})^2 + 1000*θ_3^2 + 1000*θ_4^2$
(其中，1000是我们随便取的一个比较大的数字）

如果我们要最小化这个 $J(θ)$，那么令 $1000*θ_3^2 + 1000*θ_4^2$最小的方法只有一个：就是令 $θ_3, θ_4$最小，那么这样一来，我们就相当于去掉了 $θ_3x^3 , θ_4x^4$这两项

这就是正则化背后的思想：参数越小，越少，意味着使用更加简单的模型

下面再举一个例子：比如我们要进行房屋价格的预测
假设有100个特征： $x_1,x_2,x_3,\cdots, x_{100}$
那么，我们的参数有101个： $θ_0, θ_1,θ_2,\cdots, θ_{100}$
现在，问题来了：在第一个例子里面，我是知道 $θ_3,θ_4$是有影响的参数，可是现在我并不知道这101个参数里面那些参数参与导致了过拟合，因此，保险的办法就是对所有参数都加上惩罚项，因此，我们要对cost function做这样的修改： $J(θ) = \frac{1}{2m} [\sum_{i=1}^m(h_θ(x^{(i)}) - y^{(i)})^2 + λ\sum_{j=1}^nθ_j^2]$
(注意：这里我们都是从1开始对θ进行惩罚，并不去惩罚 $θ_0$）

最后，正则化参数λ不能取得太大了，否则对所有参数的惩罚力度太大，将导致模型变成： $h_θ(x) = θ_0$，这就变成了欠拟合了

3. 线性回归中的正则化

还记得我们正则化里面的代价函数吗？ $J(θ) = \frac{1}{2m} [\sum_{i=1}^m(h_θ(x^{(i)}) - y^{(i)})^2 + λ\sum_{j=1}^nθ_j^2]$

而现在，我们来讨论一下这种代价函数的梯度下降法：
在梯度下降法中，我们做的是：
Repeat
{
$θ_0 := θ_0 - α[\frac{1}{m}\sum_{i=1}^m(h_θ(x^{(i)}) - y^{(i)})x_0^{(i)}]$
$θ_j := θ_j - α[\frac{1}{m}\sum_{i=1}^m(h_θ(x^{(i)}) - y^{(i)})x_j^{(i)} + \frac{λ}{m}θ_j]$
}
现在，我们对式子： $θ_j := θ_j - α[\frac{1}{m}\sum_{i=1}^m(h_θ(x^{(i)}) - y^{(i)})x_j^{(i)} + \frac{λ}{m}θ_j]$
做一些合并： $θ_j := θ_j(1 - α\frac{λ}{m}) - α[\frac{1}{m}\sum_{i=1}^m(h_θ(x^{(i)}) - y^{(i)})x_j^{(i)}]$
而通过数学知识我们知道： $1 - α\frac{λ}{m}$ < 1

4.逻辑回归中的正则化

还记得我们在逻辑回归中使用的代价函数吗？ $J(θ) =-[ \frac{1}{m}\sum_{i=1}^my^{(i)}logh_θ(x^{(i)}) + (1-y^{(i)})log(1-h_θ(x^{(i)}))]$
而现在我们要做的，也只是在上面这个损失函数的后面加上一个正则化项： $J(θ) =-[ \frac{1}{m}\sum_{i=1}^my^{(i)}logh_θ(x^{(i)}) + (1-y^{(i)})log(1-h_θ(x^{(i)}))] + \frac{λ}{2m}\sum_{j=1}^nθ_j^2$

那么，对于梯度下降法：
Repeat
{
$θ_0 := θ_0 - α[\frac{1}{m}\sum_{i=1}^m(h_θ(x^{(i)}) - y^{(i)})x_0^{(i)}]$
$θ_j := θ_j - α[\frac{1}{m}\sum_{i=1}^m(h_θ(x^{(i)}) - y^{(i)})x_j^{(i)} + \frac{λ}{m}θ_j]$
}