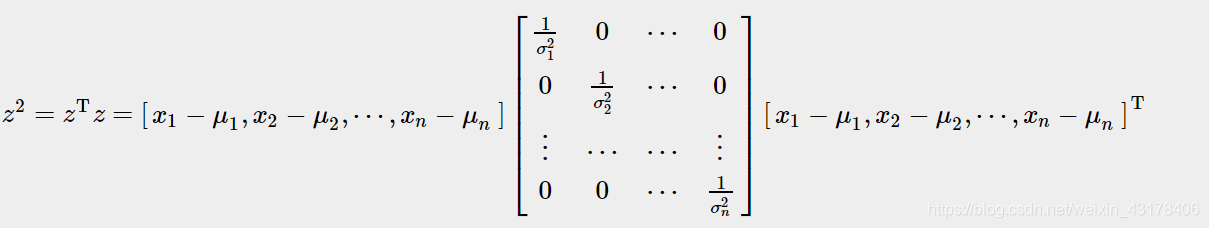1. 一元高斯分布
高斯分布(一般指一元高斯分布)又称为正态分布,是常见的连续概率分布。
假设随机变量X~
N(μ,σ2),则称变量X服从均值为
μ,方差为
σ2的正态分布。如X代表高三一班的数学成绩,则表明高三一班n名同学的数学成绩均值为
μ,方差为
σ2。
高斯分布的概率密度函数为:
f(x)=σ2π
1e−2σ2(x−μ)2
正态分布的概率密度函数为钟形,因为被称为钟形曲线。标准正态分布是位置参数
μ=0,尺度参数
σ2=1的正态分布。
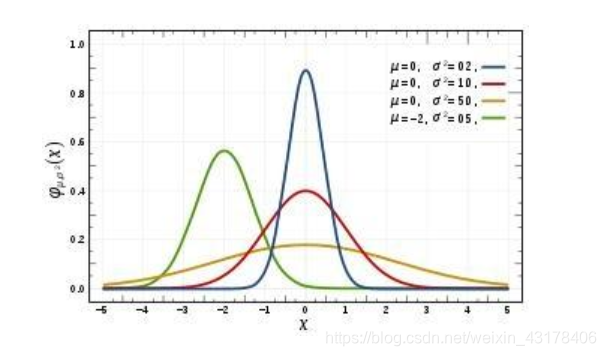
高斯分布的重要性质:
- 密度函数关于平均值对称
- 平均值与他的众数、中位数为同一值
- 函数曲线下68.268949%的面积在平均数左右的一个标准差范围内
- 95.449974%的面积在平均数左右两个标准差
2σ的范围内
- 99.730020%的面积在平均数左右三个标准差
3σ的范围内
- 函数曲线的拐点(inflection point)为离平均数一个标准差距离的位置。
2. 多元高斯分布
2.1 独立多元正态分布
假设n个变量
X=[X1,X2,...,Xn]互不相关,且服从正态分布(维度不相关多元正态分布),各个维度的均值
E(X)=[μ1,μ2,...,μn]T,标准差为
σ(X)=[σ1,σ2,...,σn]T。
联合概率密度公式:(独立分布假设下)
f(x)=p(x1,x2,...xn)=p(x1)p(x2)...p(xn)=2
πσ1σ2...σn1e−2σ12(x1−μ1)2−2σ22(x2−μ2)2−...−2σn2(xn−μn)2
如果令
σ1σ2...σn=σz
σ12(x1−μ1)2+σ22(x2−μ2)2+...+σn2(xn−μn)2=z2
那么独立多元高斯分布的密度函数可以简写如下:
f(x)=(2π
)nσz1e−21z2
对上述做一个小结:


此外,多元独立高斯分布还有明显的几何思想,可以从矩阵的角度考虑
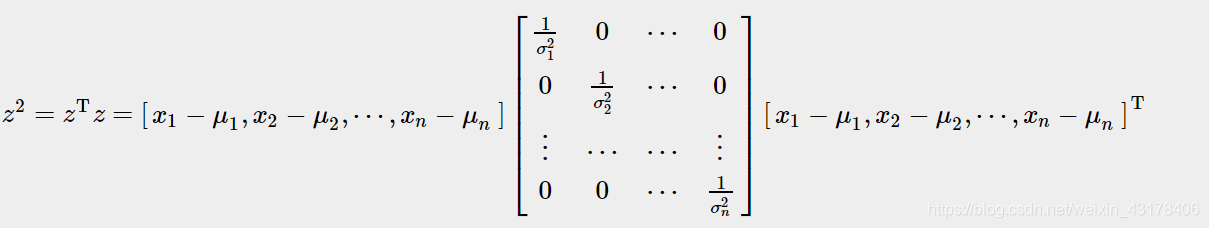
将以上等式做变量替换:


对角阵的行列式=对角元素相乘,因此
σz=∣∑∣21=σ1σ2...σn
替换变量后,等式可以简写为:
zTz=(x−μx)T∑−1(x−μx)

2.2 相关多元正态分布
相关多元正态分布不太常用,简单思想为:转换坐标轴,使其成为不相关的,然后套用公式,具体可见链接:https://www.cnblogs.com/bingjianing/p/9117330.html
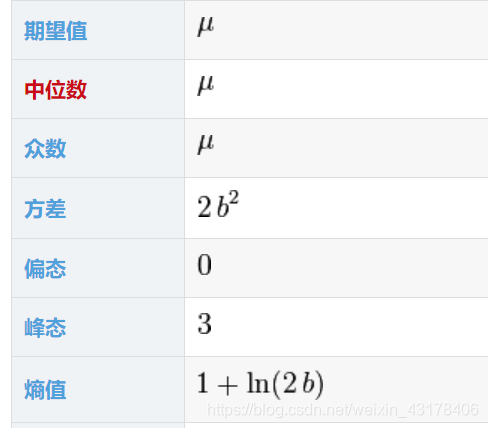
3. 一元拉普拉斯分布
一元拉普拉斯(laplace)也叫双指数分布,可以和正态分布进行对比,其密度函数为:
2σ1e−∣σx−u∣
其中
σ为尺度参数;
μ为位置参数
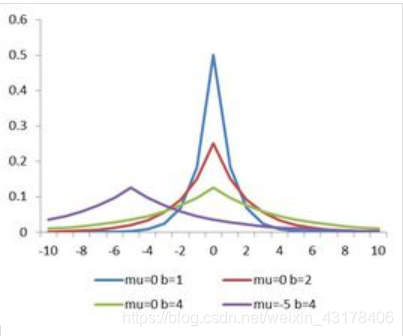
- 拉普拉斯分布关于
μ对称,并达到最大值
2σ1,因此是众数
多元laplace分布推导参照多元正态分布,此处不再叙述。