机器学习——HMM(隐马尔可夫模型的基本概念)(一)

【开始之前】由于隐马尔可夫模型属于机器学习中比较难也比较重要的知识，所以此算法笔者将分段讲解，本文主要讲的是隐马尔可夫模型的定义以及相关例子，在后续的文章中会讲到概率计算方法如前向算法、后向算法、学习算法如Baum-Welch算法、预测算法如维特比算法，敬请期待！

一、隐马尔可夫模型的定义

隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔科夫链随机生成的状态序列，成为状态序列（state sequence）；每个状态生成一个观测，而由此产生的观测的随机序列，成为观测序列（observation sequence）。序列的每一个位置又可以看作是一个时刻。隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。
隐马尔可夫模型的形式定义如下：
设Q是所有可能的隐藏状态的集合，V是所有可能的观测状态的集合：
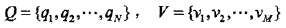
在这里插入图片描述
其中，N是可能的隐藏状态数，M是所有的可能的观察状态数。
I是长度为T的状态序列， O是对应的观察序列：

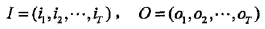
A是状态转移概率矩阵：

其中：

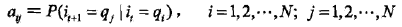
是在时刻 t 处于状态 $q_i$ 的条件下在时刻 t+1 转移到状态 $q_j$ 的概率。

B是观测概率矩阵：
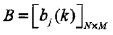
在这里插入图片描述
其中，

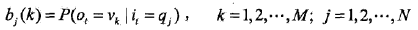
是在时刻 t 处于状态 $q_i$ 条件下生成观测 $v_k$ 的概率。

π是初始状态概率向量：
其中，
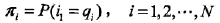
在这里插入图片描述
是时刻 t=1处于状态 $q_i$ 的概率。
隐马尔可夫模型模型，由隐藏状态初始概率分布π, 状态转移概率矩阵A和观测状态概率矩阵B决定。\pi和A决定状态序列，B决定观测序列。因此，隐马尔可夫模型 $\lambda$ 可以用三元符号表示，即
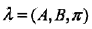
在这里插入图片描述

二、隐马尔可夫模型的例子

1、盒子和球模型

假设有4个盒子，每个盒子都装有红、白两种颜色的球，盒子里的红、白球数由下表给出。
在这里插入图片描述
按照下面的方法抽球，产生一个球的颜色的观测序列：
（1）开始，从4个盒子里以等概率随机选取1个盒子，从这个盒子里随机抽取一个球，记录其颜色后，放回；
（2）然后，从当前盒子转移到下一个盒子，规则是：如果当前盒子是盒子1，那么下一个盒子一定是盒子2；如果当前盒子是盒子2或3，那么分别以概率0.4和0.6转移到左边或右边的盒子；如果当前是盒子4，那么各以0.5的概率停留在盒子4或转移到盒子3；
（3）确定转移的盒子后，再从这个盒子里随机抽出1个球，记录其颜色，放回：
（4）如此下去，重复进行5次，得到一个球的颜色的观测序列： O = (红，红，白，白，红)

在这个过程中，观察者只能观测到球的颜色的序列，观测不到球是从哪一个盒子取出的，即观察不到盒子的序列。
在这个例子中有两个随机序列，一个是盒子的序列（状态序列），一个是球的颜色的观测序列（观测序列）。前者是隐藏的，只有后者是可观测的。这是一个隐马尔可夫模型的例子。根据所给条件，可以明确状态集合、观测集合、序列长度以及模型的三要素。

盒子对应状态，状态的集合是： Q = {盒子1，盒子2，盒子3，盒子4 } ， N = 4

球的颜色对应观测。观测的集合是： V = {红，白} ，M = 2

状态序列和观测序列长度T = 5.

初始概率分布为
在这里插入图片描述
状态转移概率分布为

观测概率分布为

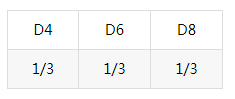
2、三骰子模型

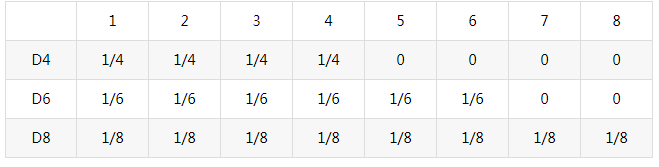
假设我手里有三个不同的骰子，第一个骰子是我们平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。
在这里插入图片描述
假设我们开始掷骰子，我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。然后我们掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。例如我们可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4

这串数字叫做可见状态链。但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链。在这个例子里，这串隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8

一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM

同样的，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率（emission probability）。就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。
在这里插入图片描述
隐含状态转换关系示意图如下：

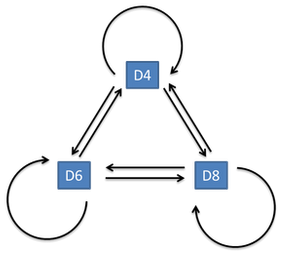
所以有：
转换概率即为状态转移矩阵A：

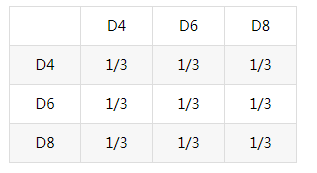
这里我们假设D4，D6，D8后面跟随任意一种筛子的概率相同，都是1/3。（实际问题中可以定义为不同概率，如D4后面出现D4，D6，D8的概率分别为1/,6，2/6，3/6）

输出概率即为观测概率矩阵B：
在这里插入图片描述
初始状态概率向量π：

Mr. Luoj

发布了38 篇原创文章 · 获赞 194 · 访问量 4734

私信关注