@
1 Logistic Regression
Logistic Regression 逻辑回归,简称LR,适合于分类问题
1.1 LR模型
对于线性回归模型,需要拟合一个\(Y=X\theta+b\)的函数,回归问题适合于连续的问题,而对于分类问题,需要得到一系列离散的标签,以二分类为例,需要预测的类别为0,1.可以使用sigmoid函数将连续问题转化为离散问题:
\[g(z) = \frac{1}{1+e^{-z}} \]
sigmoid函数的图像为:
其中,\(z \to +\infty\)时,\(g(z) \to 1\),\(z \to -\infty\) 时,\(g(z) \to 0\). Sigmoid函数的导数为:
\[g'(z)=g(z)(1-g(z))\]
令\(z=\theta x+b\),则有:
\[h_\theta(x) = \frac{1}{1+e^{-\theta x+b}}\]
对于二分类问题,该函数的输出可以理解为分类为1的概率,如果把X记为\([x^{(1)},x^{(2)},...,x^{(m)}]\), \(\theta\)记为\([\theta_1,\theta_2,...,\theta_m]\)为要估计的模型参数,则LR的矩阵形式为:
\[h_\theta(X) = \frac{1}{1+e^{-\theta X^T+b}}\]
1.2 损失函数
由于\(h_\theta (x)\)表示的是被分类为1的概率,而被分类为0的概率则为\(1-h_\theta(x)\),对于离散随机变量,我们可以写出分布列:
|y| 1 | 0|
|--|--|--|
| |\(h_\theta (x)\)| \(1-h_\theta(x)\)
用一个式子表示就是
\[p(y|x,\theta) = h_\theta(x)^y(1-h_\theta(x))^{1-y}\]
这就是\(y\)的分布函数,函数中的\theta表示要估计的参数,熟悉概率论的都知道,要估计分布函数中的参数可以有矩估计和极大似然法两种,这里选极大似然法,也叫最大似然法,这里把他的概念写出来:

也就是说,假设所有的训练样本\(y_1,y_2,..,y_m\)所对应的随机变量\(Y_1,Y_2,Y_m\)是独立同分布的,其分布函数为\(p(y|x,\theta)\),独立同分布的随机变量的联合分布函数就是每个分布函数的乘积,把这个联合分布函数称为似然函数,表示为:
\[L(\theta) = \prod_{i=1}^{m}h_\theta(x^{(i)})^{\hat{y}^{(i)}}(1-h_\theta(x^{(i)}))^{1-\hat{y}^{(i)}} \]
因为似然函数取对数后达到最大值时候的\(\theta\)与本身达到最大值后的\(\theta\)是相同的,即:
\[\argmax L(\theta) = \argmax \log [L(\theta)] \]
所以我们一般用对数似然函数,似然函数取反就是损失函数,而最大化似然函数就是最小化损失函数:
\[J(\theta) = - \ln L(\theta)=-\sum_{i=1}^{m} \hat{y}^{(i)}\ln h_\theta(x^{(i)})+(1-y^{(i)}) \ln (1-h_\theta(x^{(i)}))\]
那损失函数什么时候取最小值呢?当然就是其导数取0的时候啦。注意这里的\(\theta\)表示m个待估计的参数\(\theta_1,\theta_2,...,\theta_m\),取极值时要求每个偏导都为0. 损失函数的矩阵表达方法为:
\[J(\theta) = -Y^T\log h_\theta(X)-(E-Y)^T \log (E-h_\theta(X))\]
其中\(E\)为单位矩阵
1.3 优化方法
对于二分类的LR,可以使用梯度下降法,坐标轴下降法,牛顿法等。梯度下降法容易理解,就是参数按照梯度减小的方向更新(形式上的推导),
\[\theta = \theta - \alpha \frac{\partial J(\theta)}{\partial \theta}\]
在LR中,我们在最开始给出了SIgmoid的导数,因此用梯度下降法更新参数可以表示为:
\[\theta = \theta -\alpha X^T(h_\theta(X)-Y)\]
而牛顿法最初是用来求解函数零点的,而极值代表一阶导数的零点,因此可以用牛顿法。记\(J'(\theta)\)为一阶偏导数,\(J''(\theta)\)为二阶偏导数,则有:
\[\theta = \theta - \alpha \frac{J'(\theta)}{J''(\theta)}\]
坐标轴下降法则是固定一个坐标,沿着另外一个坐标寻找最优点,适合于导数不连续的情况。
1.4 Regulization(正则化)
为什么要正则化,这是因为机器学习模型中,学习到的参数\(\theta\)是直接与特征向量\(X\)相乘的,如LR中有:
\[h_\theta(x) = \frac{1}{1+e^{-\theta x+b}}\]
在\(X\)不变的情况下,如果\(\theta\)特别大,那乘积就会特别大,假如在测试的时候,某个测试样本跟训练样本的分布不太一样,那么经过参数\(\theta\)放大后可能得到一个非常离谱的值。参数的取值过大会让模型异常敏感,也容易过拟合,那么如何避免这种情况呢?一种可行的方法就是,我们不希望学习到的参数\(\theta={\theta_1,\theta_2,...,\theta_m}\)取值太大,那就让他们尽量接近于0,即:
\[\min \sum_{i=1}^{m} ||\theta_i||\]
矩阵表达就是\(\min ||\theta||_1\),我们称为L1正则项,同样的,也有L2正则项,
\[\frac{1}{2}||\theta||_2^2=\frac{1}{2}\sum_{i=1}^{m} ||\theta_i||^2\]
因为正则项也是关于\(\theta\)的函数,也是我们要优化的目标之一(目标是让它最小),这样就可以合并到损失函数中:
\[J(\theta) = -Y^T\log h_\theta(X)-(E-Y)^T \log (E-h_\theta(X))+\lambda_1 ||\theta||_1\]
\(\lambda_1\)是正则项的权重。加入正则项后,学习到的参数就不会太大,模型也就没那么敏感。当然,如果正则项的权重过大,那所有的参数\(\theta\)会很小,模型会异常不敏感,基本所有的输入都会得到一个差不多的输出,所有这个权重也要仔细考虑。
此外,由于\(b\)是直接加到优化函数后的,相当于对函数做平移,我们并不需要正则化这个参数。
1.5多元逻辑回归
多元逻辑回归是二元情况的推广,每个类的概率用Softmax函数计算。假设要分K类,每个要学习的参数为\((\theta_1,b_1),(\theta_2,b_2)...,(\theta_k,b_k)\) 记
\[z_1 = \theta_1x+b_1 \\ z_2 = \theta_2x+b_2 \\ ...\\ z_k = \theta_kx+b_k \]
则x属于每个类的概率可以计算为:
\[ y_1 = \frac{e^{z_1}}{\sum_{i=1}^{k}e^{z_k}} \\ y_2 = \frac{e^{z_2}}{\sum_{i=1}^{k}e^{z_k}} \\ ... \\ y_k = \frac{e^{z_k}}{\sum_{i=1}^{k}e^{z_k}} \\ \]
如下图:
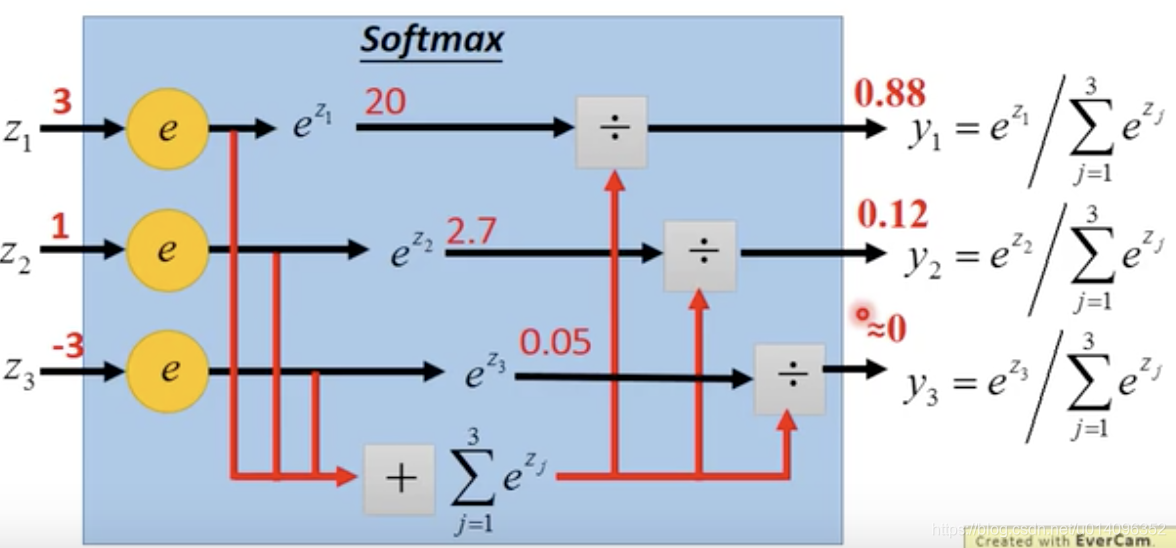
softmax其实就相当于把输入放大后再做归一化。
在多个类计算损失函数时,用到的是多个类的entropy,这时要用到One-hot矩阵,也就是:
\[ \hat{y}_1=\begin{pmatrix} 1 \\ 0 \\ ... \\ 0 \end{pmatrix} \hat{y}_2=\begin{pmatrix} 0 \\ 1 \\ ... \\ 0 \end{pmatrix} \hat{y}_k=\begin{pmatrix} 0 \\ 0 \\ ... \\ 1 \end{pmatrix} \]
具体计算的时候,使用:
\[\min -\sum_{i=1}^{k} \hat{y}_i \ln y_i\]
1.6 总结
自己的实验数据集中有23万条数据,从结果看,LR的准确率算很高的,最关键的是训练速度很快。