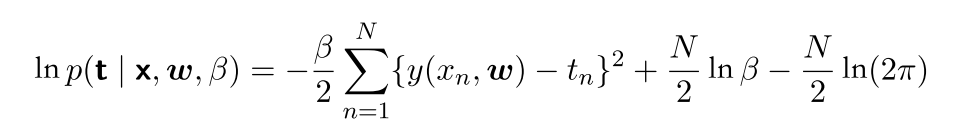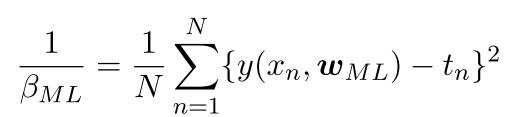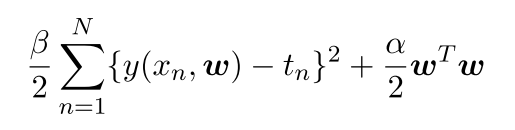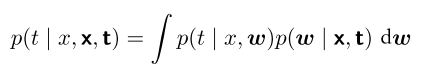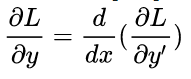模式识别 chapter 1

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/Hesy_H/article/details/101567078

summary从贝叶斯看及机器学习 – 总体思路

• 这里纠正一点，其实在MLE里面，f(x|θ)已经不是分布函数了，就是直接从给输出到输出的映射了
• 注意，这里的P(x~|D)你可以理解为新的数据的概率分布(纯inference)然后做概率到决策的映射(decision which is not discussed in this chapter )，也可以理解为输出的就是x~ 对应的tag(回归问题中是连续变量，分类问题中是离散变量)的分布【似乎更多的时候采用的思路是后者 】
• 这里我们可以看到，我们并没有说具体的f(x|θ) ( 有的地方也写作f(x;θ)或者f(x;w) ) 是什么（在整套思想中，f(x;θ)是什么并不影响整个流程 [ 所以后面我们可以看见讲贝叶斯预测/贝叶斯思想运用到线性回归问题等，实际上线性回归问题就是把f(x;θ)建模成一个线性函数而已 ] ）

混淆点

• MAP和MLE其实都求了具体的θ出来，但是MAP有用先验信息，所以还是贝叶斯学派，但是仍然不是标准的贝叶斯估计，切记，贝叶斯估计要得到就是后验概率(which MAP为了简化计算绕过去了= =把精华绕过去了2333 )
• 而且无论是贝叶斯学派还是频率学派，其实都有要求分布是有参数形式的，i.e.P(x|θ)是可以用参数形式写出来的(比如高斯分布)，区别就在于标准的贝叶斯估计(MAP不是标准的贝叶斯估计)不需要求具体的θ
• 似然函数是统计学共有的思想，只有最大似然才是频率学派的思想 （贝叶斯估计中也用到了似然函数以计算后验概率鸭）

MLE详解–Frequentist观点

refer @ https://zhuanlan.zhihu.com/p/81132832

• 对于似然函数的理解：
  

最大似然的特点（2个 including 缺点）

• 认为θ是一个常值 （贝叶斯学派认为θ是一个变量）
• 也是缺点，容易过拟合，理由如下：
  真实世界的方差并不是无偏估计，且被低估了
  • 这三个小数据集，总体的mean是和真实的mean一致的，但是由于低估了真实样本的variance，所以引入了bias
  • 由于variance太大导致了小数据集出现了bias
    
    
• 还有值得注意的一点就是：曲线拟合问题中（也就是回归问题中)，MLE蕴含了“最⼩化由公式定义的平⽅和误差函数”的思想，解析如下：

本书中，MLE的对数似然函数的形式:

对于确定w的问题来说，最⼤化似然函数等价于最⼩化由 公式（1.2）定义的平⽅和误差函数。，最⼤化似然函数等价于最⼩化由公式定义的平⽅和误差函数。
进一步，对β（标准差的倒数）求偏导并令其为0求极值，可以得到如下式子：

–》实际上就是 平⽅和误差函数 = =

• 其实我觉得书上没有让我很懂，b站这个讲得不错：
  出发点： 我们从概率中的频率学派角度来看看这个问题
  结论是：
  最小二乘估计实际上蕴含了MLE的思想 【与线性回归模型无瓜】
  有高斯噪声的最小二乘估计实际上就是MLE
  

• 注意，MLE部分构造的损失函数是对数损失函数，推出了最小二乘估计的形式

  • 这里是在线性回归的模型背景下推导的，实际上在别的模型下推导是一样的（仔细看下，把w^TX换成e^x之类的形式完全不会影响最后的结果 ) 所以与线性回归无瓜，只不过这里讲线性回归的时候正好讲到了最小二乘
  • 只能说最小二乘是很适合用于线性回归的，并不是只能用这一种损失函数

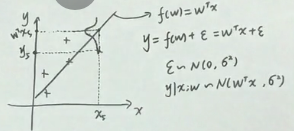
• 这里有个不理解的地方就似乎：为什么那里的高斯分布的均值就是w^Tx
  解决了：

这里y满足高斯分布没话说(w和噪声都是高斯), 然后画出的就是这个图，从似然函数角度认为已经发生的事情就是最大概率的，所以这个点对应的y就在y峰值的这条线上

• 同时我们也可以看到，解出来的解析解是这样的：
  
  如果当X^TX没有逆的情况下就很棘手，所以后面要引入正则化项，保证可以括号内是一个必定能求逆的情况( X^TX是一个半定矩阵，半定矩阵加上一个正定的对角矩阵，则为正定，必定可逆)

$x^T(AA^T)x = (A^Tx)^T (A^Tx) = ||A^Tx||^2 >=0$ 实矩阵和自己本身的转置相乘得到半定矩阵

MAP详解–Bayesian观点

• P27 在⾼斯噪声的假设下，平⽅和误差函数是最⼤化似然函数的⼀个⾃然结果【曲线拟合问题中（也就是回归问题）】
• 其实MLE和MAP相差不多 只不过MAP是贝叶斯学派 引入了先验概率P(w)
  
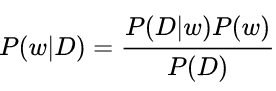
  其中的P(D|w)则是似然函数

缺点

• prior distribution is often selected on the basis of mathematical convenience rather than as a reflection of any prior beliefs。例如常选择conjugate prior ( 共轭先验 )【这个应该是标准贝叶斯的缺点233 】

• 还有值得注意的一点就是：MAP蕴含了“最⼩化期望风险的思想，解析如下：

最⼤化后验概率等价于最⼩化正则化的平⽅和误差函数（之前在公式（1.4）中提 到），正则化参数为λ = α/β。

同样的，这里其实我也没有很懂，b站这个讲得不错：
出发点： 我们从概率中的贝叶斯学派角度来看看这个问题
结论是：
先验分布为均值为0的GD(高斯分布)的MAP就是带有高斯噪声的LSE
那么我们首先就是要求人家的后验，所以就从p(w|y)开始推导起来，其中为了计算方便，给w的分布也设定成N(0,sigma²)

求着求着就发现可以从MAP推导处带惩罚项的最小二乘了。

• 岭回归的参数值就是高斯噪声的方差与先验分布的方差的比值 【然而这两个我们都不知道，但是书p28表明这个式子我们是可以从数据里面推出来的！！！】
• L(w)(loss)改成J(w)是因为此时加上了penalty，再叫成损失函数不太合适了

Bayesian方法面临的主要问题：marginalization计算困难

• 所以MCMC、概率图之列的的motivation就出来了
  • 即使有了MAP，也会有些问题
    
    
    
    
    

tip

• 多维高斯分布的性质在2.3节介绍
• 观测数据集x = (x₁,x₂,L,x_N)^T
  向量变量 $x$ = (x₁,x₂,L,x_N)^T
  要区分这两个符号
• ML 其实是max likelihood 最大似然

---

question

• 14 这里w0为什么不加入惩罚项里面 等待挖坟
  
  
  
• 28 超参数的定义是啥 控制模型参数分布的参数又是啥

这里方框括起来的不是一个条件概率分布，而是一个概率分布，不过意味着w的分布中有参数用α表示。
然后就引出了超参数的定义

这里的α是一个向量，是w各维度上方差的倒数，又称为精度

• 28 推导

实际上这个是
p(t | $x$,x,t)= $\int$p(t, $w$ | $x$,x,t) d $w$ = $\int$p(t | $w$, $x$,x,t) p( $w$|x,t)d $w$= $\int$p(t | $w$, $x$) p( $w$|x,t)d $w$
最后一步是因为 w包含了x和t的信息( 和p( $w$|x,t) 相乘的情况下)，这时候信息冗余，就可以把x和t略去不写了

• MLE有误差最小化的思想，MAP有风险结构最小化的思想【看看李航怎么写的】
• 29 流形？ 似乎和GAN那些还有点关联 还有自由度的概念= =
  
  
• 38 变分法求解

变分法实际上就是: 其中y=f(x)

• 40 那个 $\delta f(x) =f(x)log(f(x))$咋推导得到的来着
• 42 非均匀分布的比均匀分布的熵要小 --》 有点难以理解了= =
• 1.6.1相对熵和互信息也没看 似乎牵扯到KL散度= =
• recursive Bayes还要仔细看下

---

第一章剩余知识及补充知识

点估计

由此引出了无偏估计之类的后续概念

• MLE和MAP都属于点估计

变量和参数之间的区别

参数是一个定值，whatever y取什么；而变量也是会变化的，和y一起变化（至于谁影响谁，看情况）

p28 超参数的定义

个人理解 ： 控制模型参数分布，是我们人为给定的参数

后验概率的重要性(用处) tl;dr

如何应对过拟合这个缺点

• 常用三种方法：

  • 增大数据量
  • 使用贝叶斯估计（ 会引入先验信息，对数据进行纠正
  • 加入正则项 【实际上就是引入先验信息的思想】
  • 降维,i.e.特征提取/特征选择

• 频率学派使用两种方法

  • regularization 加入正则项
  • cross-validation

• 贝叶斯学派使用两种方法;

  • 引入先验 【实际上对应的就是加入正则项】

决策 p36

• 分为inference和decision阶段，inference阶段获得了后验概率，决策阶段就根据后验概率进行分类

37 三种方式做出决策

其实觉得知乎这个讲得也很清楚 https://www.zhihu.com/question/20446337

• 生成方法学习到的就是生成模型（SVM、MAP、神经网络） 判别方法学习到的就是判别模型( 朴素贝叶斯、贝叶斯网络之类 )

• 生成式模型 ---- 对联合分布进行建模【贝叶斯 要求分母的积分，实际上P(D)就是P(x,t) [ 同理，P( $t$ | $x$,x,t ) 也可以看作是P( $x$ | D ) ]，这样一来不同版本之间的知识就能贯通了 】 ， 然后得到后验概率（注意，这里的后验概率是P( $x$ | D ) ,而不是P(θ|D),我们是通过P(θ|D)求得的P( $x$ | D )，在求P(θ|D)这个过程中求了P(D) ），再用决策论将后验概率映射到决策上【这个是最难的 fully bayes】
• 判别式模型 ( poor man’s Bayes) ---- 也要得到后验概率（P( $x$ | D ),i.e.P( $t$ | $x$,x,t ) ），但是不需要对联合分布进行建模，相当于对后验概率进行建模 ，输入x输出一个后P( $t$ | $x$ )，然后再执行decision 部分【MLE属于这种；MAP也属于这种，绕过了分母积分的步骤也就是绕过了积分的步骤 】
• 判别函数 ----不需要对联合分布进行建模，也不需要得到后验概率，直接建立输入到输出的映射 [ 把推断和决策合在一起做了 ]【like神经网络，支持向量机etc】
• 总结：我们很多情况下还是需要获得后验概率的which means 生成式模型is prefered

回归函数的损失函数

我们要求一个y（x）使得ELoss最小，如下:

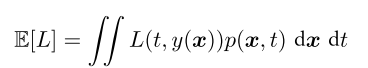
如果L(t,y(x))采用的是平方和的形式则可以推导出如下形式

1.6 信息论

信息量和熵 很有趣的看法

对于熵的看法很有趣
h(x) 用于定义信息量，其中看出h(x) 应该和p(x)具有如下的关系：

关于信息量的理解 ，我觉得这个说得也很透彻：

那么对于一个随机变量，其传送的信息量大小就是（这里用期望表示 毕竟这是个随机变量啊！）：

这个量又被称为随机变量的熵。

用信息量来理解熵真的很棒

一个重要的性质：

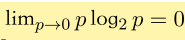
从信息量的角度来看，一个很反直觉的结论：非均匀分布的比均匀分布的熵要小

• 43 拉格朗日惩罚项的求解

  • 先用拉格朗日乘子把约束方程放到不等式里面去，然后求偏导为0的情况，然后回代到约束条件（方程形式）里面去，可以求得拉格朗日乘子的大小

• 离散熵最大的情况下，对应的分布是均匀分布，那么微分熵最大的情况下呢？
  我们把p(x)看作一个泛函，然后利用变分法求解微分熵最大时的p(x)，得到p(x)实际上是一个高斯分布
  于是我们看看高斯分布的熵到底是什么，得到：
  
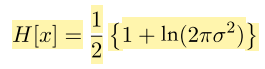
  发现 微分熵居然可以是负的（离散熵只能是正的）