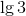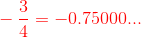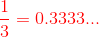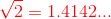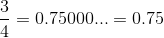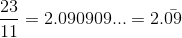Chapter1 Preliminaries

版权声明：作者微信 2992860292, QQ同号 https://blog.csdn.net/qq_40723748/article/details/85268334

1.1Real numbers and the real line

Real Numbers

Much of calculus is based on properties of the real number system. Real numbers are numbers that can be expressed as decimals, such as

The dots in each case indicate that the sequence of decimal digits goes on forever. Every conceivable decimal expansion represents a real number, although some numbers have two representations. For instance, the infinite decimals and represent the same real number 1. A similar statement holds for any number with an infinite tail of 9’s.

The real numbers can be represented geometrically as points on a number line called the real line.

The symbol R denotes either the real number system or, equivalently, the real line. 

The properties of the real number system fall into three categories: algebraic properties, order properties, and completeness. The algebraic properties say that the real numbers can be added, subtracted, multiplied, and divided (except by 0) to produce more real numbers under the usual rules of arithmetic. You can never divide by 0. 

The order properties of real numbers are given in Appendix 4. The following useful rules can be derived from them, where the  symbol means “implies.”

Notice the rules for multiplying an inequality by a number. Multiplying by a positive number preserves the inequality; multiplying by a negative number reverses the inequality. Also, reciprocation reverses the inequality for numbers of the same sign. 

The completeness property of the real number system is deeper and harder to define precisely. However, the property is essential to the idea of a limit (Chapter 2). Roughly speaking, it says that there are enough real numbers to “complete” the real number line, in the sense that there are no “holes” or “gaps” in it. Many theorems of calculus would fail if the real number system were not complete. The topic is best saved for a more advanced course, but Appendix 4 hints about what is involved and how the real numbers are constructed. 

We distinguish three special subsets of real numbers. 

1. The natural numbers, namely 1, 2, 3, 4,...

2. The integers, namely ,...

3. The rational numbers，namely the numbers that can be expressed in the form of a fraction m/n, where m and n are integers and n0. Examples are ,  .

The rational numbers are precisely the real numbers with decimal expansions that are either

(a) terminating (ending in an infinite string of zeros), for example,

or 

(b) eventually repeating (ending with a block of digits that repeats over and over), for example 

(The bar indicates the block of repeating digits.)

A terminating decimal expansion is a special type of repeating decimal since the ending zeros repeat. 

The set of rational numbers has all the algebraic and order properties of the real numbers but lacks the completeness property. For example, there is no rational number whose square is 2; there is a “hole” in the rational line where 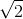 should be. 

Real numbers that are not rational are called irrational numbers. They are characterized by having nonterminating and nonrepeating decimal expansions.  Examples are  and . Since every decimal expansion represents a real number, it should be clear that there are infinitely many irrational numbers. Both rational and irrational numbers are found arbitrarily close to any point on the real line.