【动态规划基础】数字金字塔

题目链接：1258：【例9.2】数字金字塔

1258：【例9.2】数字金字塔

时间限制: 1000 ms 内存限制: 65536 KB
提交数: 9635 通过数: 5467

【题目描述】

观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。

在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。

【输入】

第一个行包含R(1≤ R≤1000)，表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

所有的被供应的整数是非负的且不大于100。

【输出】

单独的一行，包含那个可能得到的最大的和。

【输入样例】

5
13
11 8
12 7  26
6  14 15 8
12 7  13 24 11

【输出样例】

提交统计信息提交记录

【动态规划基础】数字金字塔

　　经典的动态规划水题

方法一：贪心

　　题目里说了，从上往下走，要求出路径的最大值，那么我最先想到的方法就是——

　　你每次都走最大的一边就可以了啊。

　　就像这样：

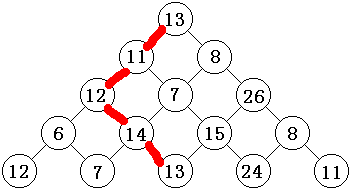
　　但是，如果你是一个善于造数据来验证你的算法的人，你很快就会发现自己算法的问题，就像这样：

　　在这一组数据中，如果使用贪心算法，就会一开始就左边，从而错失下面全是9的右边。

　　也就是说，贪心算法看得太近了，没有顾全大局。

方法二：搜索 & 记忆化搜索

　　像我这样的暴力型选手，碰见什么题都要用搜索写一遍。可以对拍不说，写不出来的时候，还可以骗分。

#include <bits/stdc++.h>
using namespace std;

int jzt[1005][1005], maxn, summ, n;

void dfs(int i, int j){
    if(i==n){
        maxn=maxn>summ?maxn:summ;
    }
    else{
        summ+=jzt[i+1][j];
        dfs(i+1, j);
        summ-=jzt[i+1][j];
        summ+=jzt[i+1][j+1];
        dfs(i+1, j+1);
        summ-=jzt[i+1][j+1];
    }
}

int main(){
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        for(int j=0; j<=i; j++){
            scanf("%d", &jzt[i][j]);
        }
    }

    dfs(0, 0);
    printf("%d", maxn+jzt[0][0]);

    return 0;
}

　　 T了。。

　　但是没关系，我们还有搜索优化利器：记忆化。

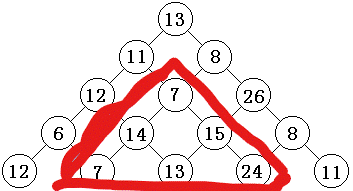
　　通过观察与推理，我们会发现，中间的这些点到底端的最优解会被重复计算，所以我们要把这些状态记忆下来，四舍五入约等于全部记下来（其实是我懒得做特判）。。

#include <bits/stdc++.h>
using namespace std;

int n, bz[1005][1005], jzt[1005][1005];

int dfs(int x, int y){
    if(x==n-1) return jzt[x][y];
    else{
        if(bz[x][y]) return jzt[x][y];
        else{
            bz[x][y]=1;
            jzt[x][y]+=max(dfs(x+1, y), dfs(x+1, y+1));
            return jzt[x][y];
        }
    }
}

int main(){
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        for(int j=0; j<=i; j++){
            scanf("%d", &jzt[i][j]);
        }
    }
    printf("%d", dfs(0, 0));

    return 0;
}

　　这次，就成功地AC了，不得不感叹记忆化的强大。其实记忆化搜索的用时就已经相当于动态规划了（这也是为什么我把搜索学好后才学动态规划）。。

方法三：动态规划（递推）

　　现在，想象一下，通过某些神奇的算法，你已经成功走到了倒数第二行的某一个位置，那么下一步应该怎么走呢？

　　很明显，只要走最大的那个就可以了。因为这里只有最后一步了，局部最优解就等于全局最优解。

　　但事实是，你并不知道这个神奇的算法。。。所以你还是不知道你会走到倒数第二行的哪个位置。

　　但是，无论如何，你最终都会走到倒数第二行的n-1个点之一。那么我们就把到任意一个点的全局最优解求出来吧。

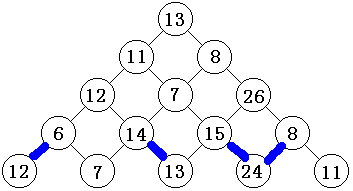
　　那么知道了倒数第二行怎么走，那么我们就再进一步吧。

通过某些神奇的算法，你已经成功走到了 n-2 行（倒数第三行）的某一个位置，那么下一步应该怎么走呢？

　　这时，我们就不能通过单纯的比大小来决定了。

　　但是，我们通过上一步的计算，已经知道了走到 n-1 行的最优解，而且，我们也可以算出来走到 n-1 行某一个位置之后走到的点的和（这里指之前算出的最优解）。

　　那么问题就很简单了，只需要走这个值最大的一边就可以了。

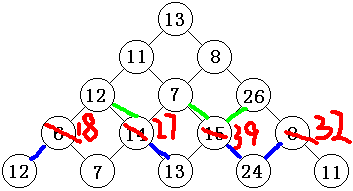
　　重复这个过程。。。

　　最后：

通过某些神奇的算法，你已经成功走到了第 1 行的某一个位置，那么下一步应该怎么走呢？

　　显然，我们已经知道了下一步该怎么走，，而且这时，我们就可以考虑这个“神奇的算法”了。

　　由于第一行只有一个数，所以我们可以肯定的是，我们走到的一定是这个位置。

　　最后，再算出第一步该怎么走时，你就算出了这个最优路径。

代码：

#include <bits/stdc++.h>
using namespace std;

int n, a[1005][1005];

int main(){
    cin >> n;
    for(int i=0; i<n; i++){
        for(int j=0; j<=i; j++){
            cin >> a[i][j];
        }
    }
    for(int i=n-2; i>=0; i--){
        for(int j=0; j<=i; j++){
            a[i][j] += max(a[i+1][j], a[i+1][j+1]);
        }
    }
    cout << a[0][0];

    return 0;
}