转载:http://redstonewill.com/1529/
普通方阵的矩阵分解(EVD)
我们知道如果一个矩阵 A 是方阵,即行列维度相同(mxm),一般来说可以对 A 进行特征分解:
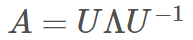
其中,U 的列向量是 A 的特征向量,Λ 是对角矩阵,Λ 对角元素是对应特征向量的特征值。
举个简单的例子,例如方阵 A 为:
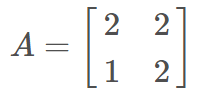
那么对其进行特征分解,相应的 Python 代码为:
1 import numpy as np 2 3 A = np.array([[2,2],[1,2]]) 4 lamda, U = np.linalg.eig(A) # 特征向量和特征值 5 print('方阵 A', A) 6 print('特征值 lamda', lamda) 7 print('特征向量 U', U) 8 9 # 输出 10 # 方阵 A [[2 2] 11 # [1 2]] 12 # 特征值 lamda [3.41421356 0.58578644] 13 # 特征向量 U [[ 0.81649658 -0.81649658] 14 # [ 0.57735027 0.57735027]]
特征分解就是把 A 拆分,如下所示:

其中,特征值 λ1=3.41421356,对应的特征向量 u1=[0.81649658 0.57735027];特征值 λ2=0.58578644,对应的特征向量 u2=[-0.81649658 0.57735027],特征向量均为列向量。
对于任意方阵,不同特征值对应的特征向量必然线性无关,但是不一定正交
对称矩阵的矩阵分解(EVD)
如果方阵 A 是对称矩阵,例如:
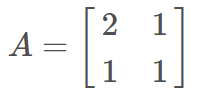
对称矩阵特征分解满足以下公式:
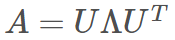
那么对其进行特征分解,相应的 Python 代码为:
1 import numpy as np 2 3 A = np.array([[2,1],[1,1]]) 4 lamda, U = np.linalg.eig(A) # 特征向量和特征值 5 print('方阵 A', A) 6 print('特征值 lamda', lamda) 7 print('特征向量 U', U) 8 9 # 输出 10 # 方阵 A [[2 1] 11 # [1 1]] 12 # 特征值 lamda [2.61803399 0.38196601] 13 # 特征向量 U [[ 0.85065081 -0.52573111] 14 # [ 0.52573111 0.85065081]]
特征分解就是把 A 拆分,如下所示:

其中,特征值 λ1=2.61803399,对应的特征向量 u1=[0.85065081 0.52573111];特征值 λ2=0.38196601,对应的特征向量 u2=[-0.52573111 0.85065081],特征向量均为列向量。
注意,我们发现对阵矩阵的分解和非对称矩阵的分解除了公式不同之外,特征向量也有不同的特性。对称矩阵的不同特征值对应的特征向量不仅线性无关,而且是相互正交的。什么是正交呢?就是特征向量内积为零。验证如下:
0.85065081∗−0.52573111+0.52573111∗0.85065081=0
重点来了,对称矩阵 A 经过矩阵分解之后,可以写成以下形式:
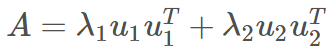
对上式进行验证:

奇异值分解(SVD)
我们发现,在矩阵分解里的 A 是方阵或者是对称矩阵,行列维度都是相同的。但是实际应用中,很多矩阵都是非方阵、非对称的。那么如何对这类矩阵进行分解呢?
因此,我们就引入了针对维度为 mxn 矩阵的分解方法,称之为奇异值分解(Singular Value Decomposition)。
假设矩阵 A 的维度为 mxn,虽然 A 不是方阵,但是下面的矩阵却是方阵,且维度分别为 mxm、nxn

因此,我们就可以分别对上面的方阵进行分解:
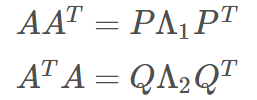
其中,Λ1 和 Λ2 是对焦矩阵,且对角线上非零元素均相同,即两个方阵具有相同的非零特征值,特征值令为 σ1, σ2, … , σk。值得注意的是,k<=m 且 k<=n
根据 σ1, σ2, … , σk 就可以得到矩阵 A 的特征值为
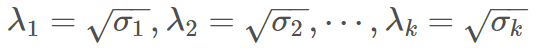
接下来,我们就能够得到奇异值分解的公式:
# 公式推导 https://www.cnblogs.com/pinard/p/6251584.html
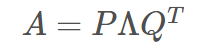
其中,P 称为左奇异矩阵,维度是 mxm,Q 称为右奇异矩阵,维度是 nxn。Λ 并不是方阵,其维度为 mxn,Λ 对角线上的非零元素就是 A 的特征值 λ1, λ2, … , λk。图形化表示奇异值分解如下图所示:

举个简单的例子来说明,令 A 为 3×2 的矩阵:
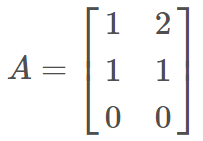
则有:
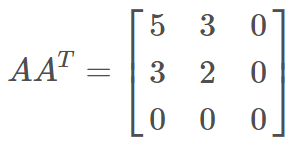
计算得到特征向量 P 和对应的特征值 σ 为:

然后,有:

计算得到特征向量 Q 和对应的特征值 σ 为:
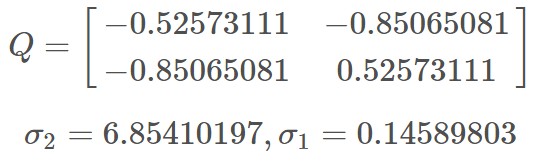
则我们看可以得到 A 的特征值为:

最后,整合矩阵相乘结果,满足奇异值分解公式。
奇异值分解可以写成以下和的形式:

其中,p1 和 q1 分别为左奇异矩阵和右奇异矩阵的特征向量。
如何形象化理解 SVD
我们对该图片进行奇异值分解,则该图片可写成以下和的形式:
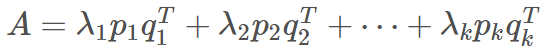
上式中,λ1, λ2, … , λk 是按照从大到小的顺序的。
首先,若我们只保留最大的奇异值 λ1,舍去其它奇异值,即 A=λ1p1q1T,然后作图,很不清晰
不断增加前面奇异值的数量,图像越来越清晰
可见,取前 50 个最大奇异值来重构图像时,已经非常清晰了。我们得到和原图差别不大的图像。也就是说,随着选择的奇异值的增加,重构的图像越来越接近原图像。
基于这个原理,奇异值分解可以用来进行图片压缩。例如在本例中,原始图片的维度是 870×870,总共需要保存的像素值是:870×870=756900。若使用 SVD,取前 50 个最大的奇异值即可,则总共需要存储的元素个数为:
(870+1+870)∗50=87050
显然,所需存储量大大减小了。在需要存储许多高清图片,而存储空间有限的情况下,就可以利用 SVD,保留奇异值最大的若干项,舍去奇异值较小的项即可。
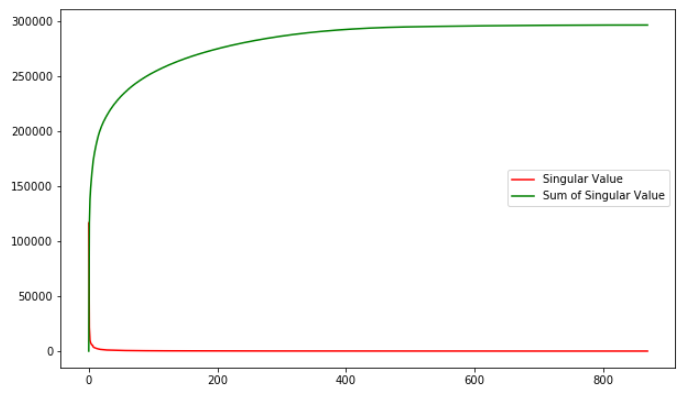
值得一提的是,奇异值从大到小衰减得特别快,在很多情况下,前 10% 甚至 1% 的奇异值的和就占了全部的奇异值之和的 99% 以上了。这对于数据压缩来说是个好事。下面这张图展示了本例中奇异值和奇异值累加的分布:
SVD 数据压缩的算法图示如下:

SVD 数据压缩的示例代码为:
1 from skimage import io 2 import matplotlib.pyplot as plt 3 from PIL import Image 4 5 img=io.imread('./ng.jpg') 6 m,n = img.shape 7 io.imshow(img) 8 plt.show() 9 10 P, L, Q = np.linalg.svd(img) 11 tmp = np.diag(L) 12 if m < n: 13 d = np.hstack((tmp,np.zeros((m,n-m)))) 14 else: 15 d = np.vstack((tmp,np.zeros((m-n,n)))) 16 17 # k = 50 18 img2 = P[:,:50].dot(d[:50,:50]).dot(Q[:50,:]) 19 io.imshow(np.uint8(img2)) 20 plt.show() 21 22 tmp = np.uint8(img2) 23 im = Image.fromarray(tmp) 24 im.save("out.jpg")
参考文献:
https://zhuanlan.zhihu.com/p/26306568
https://www.zhihu.com/question/22237507/answer/53804902