现代通信原理2.4：常用信号的傅立叶变换

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/tanghonghanhaoli/article/details/97400306

1、复频谱

  一般来说，我们采用复频谱，它有两种表示形式，即

• 正交形式
  $G(f)=X(f)+jY(f)$
• 幅度-相位形式
  $\begin{aligned} G(f)&=|G(f)|e^{j\theta f}\\ G(f)&=\sqrt{X^2(f)+Y^2(f)}\\ \theta (f)&=\tan^{-1}\left[\frac{Y(f)}{X(f)}\right]. \end{aligned}$需要注意的是，尽管有时候我们会碰上虚部为零的频谱，但更一般情况下遇到的都是复频谱。因此在画频谱图的时候就需要注意，我们需要用两张图才能够表示一个实部、虚部都不为零的频谱，当然既可以用实部-虚部，也可以用幅度-相位。

2、傅立叶变换常用性质

  傅立叶变换性质有很多。我们这里只罗列几种课程中经常会遇到的。

• 时延
  $\begin{aligned} g(t)&\leftarrow\rightarrow G(f)\\ g(t-t_0)&\leftarrow\rightarrow G(f)e^{-j2\pi ft_0} \end{aligned}$
• 频移
  $\begin{aligned} g(t)&\leftarrow\rightarrow G(f)\\ g(t)e^{j2\pi f_0t}&\leftarrow\rightarrow G(f-f_0) \end{aligned}$
• 对偶性
  $\begin{aligned} g(t)&\leftarrow\rightarrow G(f)\\ G(t)&\leftarrow\rightarrow g(-f) \end{aligned}$

3、冲激信号与直流信号

3.1 冲激函数

  冲激函数可以看成是某种脉冲函数的极限形式。
  如图1所示，有一宽为 $a$，高为 $\frac{1}{a}$，面积为1的矩形脉冲波形。若将 $a$逐渐减小，保持面积不变，则高度不断增加。极限情况下， $a \rightarrow 0$，则高度 $\frac{1}{a}$趋近于无穷大。这样的函数就称为冲激函数。当然其它形式的脉冲函数，也可以逼近冲激函数，只要面积保持为1，我们就称为单位冲激函数，用 $\delta(x)$表示，因此我们有
$\delta(x)=\left\{\begin{aligned} 1,&\quad x=0\\ 0,&\quad x=\not 0. \end{aligned} \right.$
由于信号的波形和频谱都有可能是冲激函数，因此我们自变量用 $x$表示，显然这里的 $x$可以是 $t$，也可以是 $f$。注意 $\delta(x)$有两个非常重要且有用的性质。

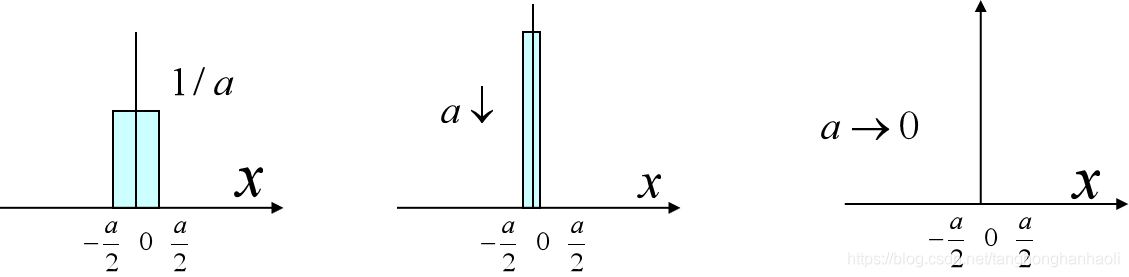
图1 矩形脉冲的极限形式

• 冲激函数的取样性质
  $g(x)\delta(x-x_0)=g(x_0)\delta(x-x_0),$这个性质说明，任何一个函数与一个冲激函数相乘，其结果还是一个冲激函数，只是强度（即面积）不再是1，而是该函数在冲激函数出现时( $x=x_0$)的幅度。这个性质在后面模拟信号数字化部分的抽样中还要用到。
• 冲激函数的筛选性质
  $\int_{-\infty}^{\infty}g(x)\delta(x-x_0)dx=g(x_0)\int_{-\infty}^{\infty}\delta(x-x_0)dx=g(x_0)$这个性质可能一下不容易看出来有什么用处。我们回忆下卷积运算，若有两个函数 $g(x)$和 $m(x)$，它们的卷积为
  $g(x)*m(x)=\int_{-\infty}^{\infty}g(\tau)m(x-\tau)d\tau.$若 $m(x)=\delta(x)$，有
  $g(x)*\delta(x)=\int_{-\infty}^{\infty}g(\tau)\delta(x-\tau)d\tau=\int_{-\infty}^{\infty}g(\tau)\delta(\tau-x)d\tau,$由筛选性质可得 $g(x)*\delta(x)=g(x)\int_{-\infty}^{\infty}\delta(\tau-x)d\tau=g(x).$因此，任何函数与冲激函数卷积，其结果就是这个函数本身。而任何一个函数与移位之后的冲激函数卷积，则为这个函数移位，即
  $\begin{aligned} g(x)*\delta(x-x_0)&=\int_{-\infty}^{\infty}g(\tau)\delta(x-x_0-\tau)d\tau\\ &=\int_{-\infty}^{\infty}g(\tau)\delta[\tau-(x-x_0)]d\tau\\ &=g(x-x_0) \end{aligned}$

3.2 冲激信号及其频谱密度

  所谓冲激信号，是指其波形为冲激函数的信号，即 $g(t)=A\delta (t)$，其中 $A$为冲激强度（即面积）。显然冲激信号并非物理可实现信号，但用它来刻画持续时间非常短，瞬时幅度非常大的信号，是非常有用的。
  下面我们来看冲激信号的频谱密度，我们可以得到傅里叶变换对
$g(t)=A\delta (t)\leftrightarrow G(f)=A,$显然，冲激信号的频谱为平坦的直线，其幅度为冲激信号的强度 $A$。冲激信号波形与频谱示意图如图2所示。

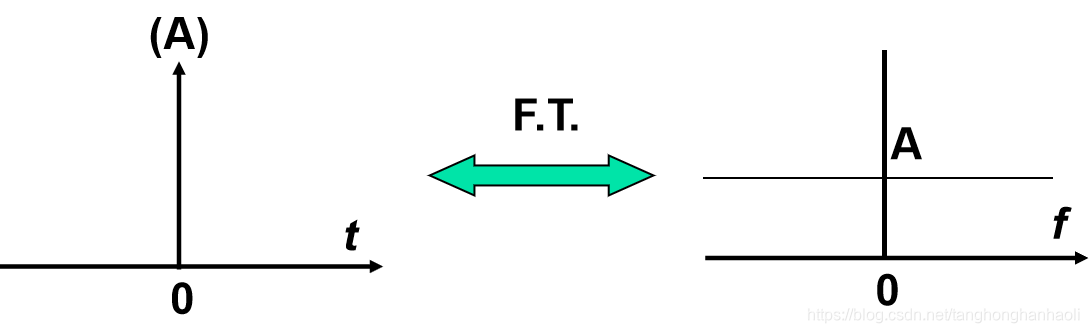
图2 冲激信号波形与频谱密度函数示意图

3.3 直流信号及其频谱密度

  若信号的频谱为冲激函数，即 $G(f)=A\delta(f)$，根据傅里叶变换的对偶性质，可以得到傅里叶变换对
$g(t)=A\leftrightarrow G(f)=A\delta(f),$其示意图如图3所示。显然，该波形为直流信号，从频域也可以看出，信号只在频率 $f=0$点处幅度不为零。

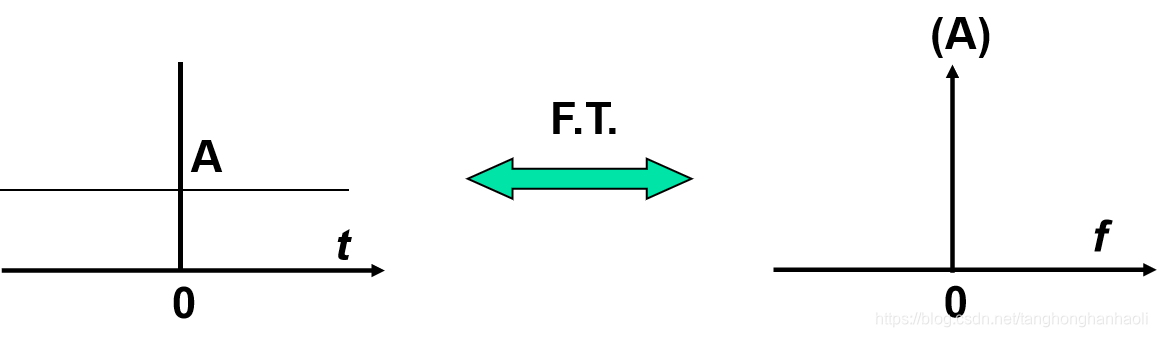
图3 直流信号波形与频谱密度函数示意图

4、单音信号的傅里叶变换

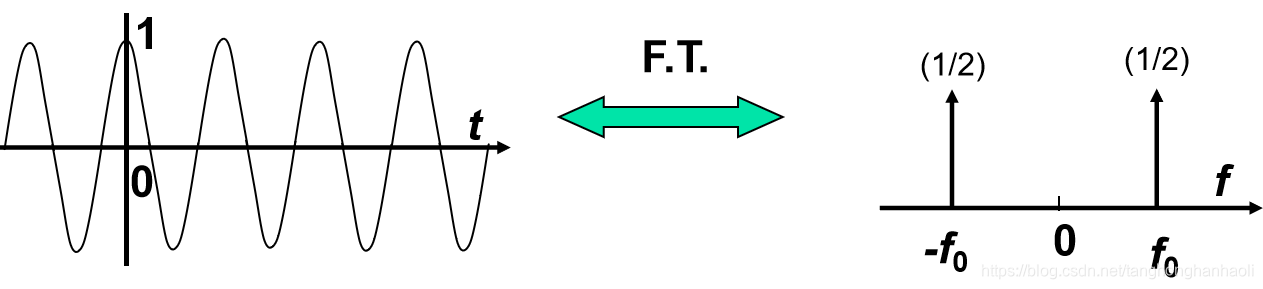
  我们先来看余弦信号的傅里叶变换，即
$g(t)=\cos(2\pi f_0t)\leftrightarrow G(f)=\frac{1}{2}\left[\delta(f-f_0)+\delta(f+f_0\right],$其波形与频谱如图4所示。从图中可以很容易看出，为何我们将余弦信号成为单音信号，因为其只具有一个频率 $f_0$。【请大家思考，为何图中有两个冲激，但我们却说它只具有一个频率？】

扫描二维码关注公众号，回复： 7199297 查看本文章

图4 余弦信号波形与频谱密度函数示意图

  除了余弦信号之外，正弦信号也是单音信号，其傅里叶变换为
$g(t)=\sin(2\pi f_0t)\leftrightarrow G(f)=\frac{1}{j2}\left[\delta(f-f_0)-\delta(f+f_0\right],$显然该频谱不再是实频谱，因此在作图时就需要用两张图来表示，即同相-正交，或者幅度-相位。

图5 正弦信号波形与频谱密度函数示意图（幅度-相位）

5、矩形脉冲信号与三角形脉冲信号

  我们用 $A{\rm Rect}\left(\frac{t-t_0}{\tau} \right)$来表示中心在 $t_0$，宽度为 $\tau$，高度为 $A$的矩形脉冲信号（有时也叫门函数，因为看起来很象门的形状）。由于门的中心在原点，因此图6中的矩形脉冲信号可以写为 $g(t)=A{\rm Rect}\left(\frac{t}{\tau}\right)$。显然矩形脉冲信号一个能量信号，因为其持续时间有限，能量为有限值。矩形脉冲信号的傅里叶变换为
$g(t)={\rm Rect}\left(\frac{t}{\tau}\right)\leftrightarrow G(f)=\tau{\rm Sa}\left(\pi f\tau\right),$其波形与频谱示意图见图6。

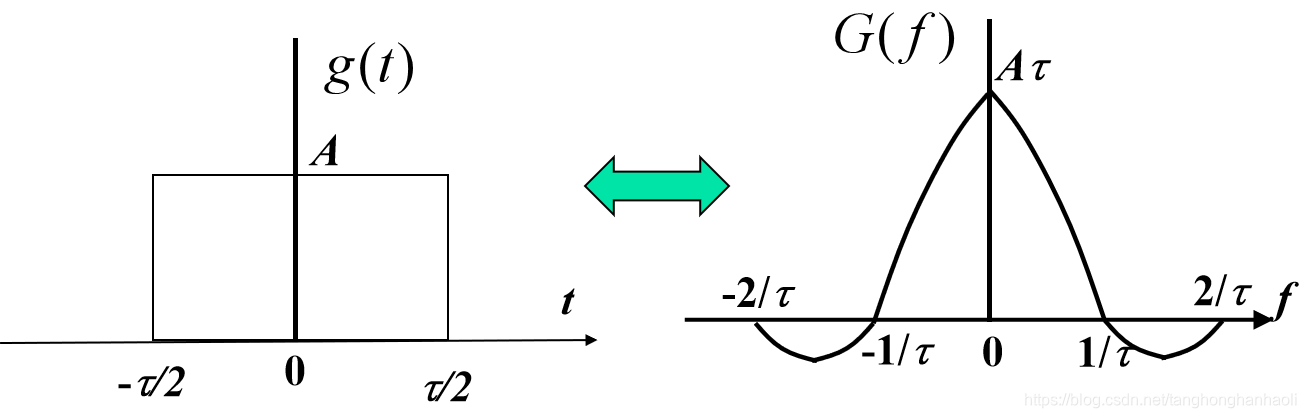
图6 矩形脉冲信号波形及其频谱密度函数示意图

---

  注意这里的函数 ${\rm Sa}(x)$称为抽样函数，它的定义式为
${\rm Sa}(x)=\frac{\sin(x)}{x},$注意我们也可以把Sa函数写成Sinc函数，二者关系为 ${\rm Sa}(\pi x)={\rm Sinc}(x)$。
  显然，当 $x=0$时，根据罗比塔法则， ${\rm Sa}(x)=1$；当 $x=k\pi$， $k$为整数且不为零时， ${\rm Sa}(x)=0$，因此 $k\pi$为Sa函数的过零点。从原点到第一过零点之间的频谱成分我们称为主瓣，第 $k$到 $k+1$个过零点之间的频谱成分我们称为旁瓣，这里 $k=\not 0$。随着 $k$的增大，旁瓣逐渐衰减。

---

  对于函数 ${\rm Sa}\left(\pi f \tau\right)$，当 $f=\frac{k}{\tau}$， $k$为整数且不为零时，函数值为零。从图6中可以看出，矩形脉冲波形的频谱密度为Sa函数，显然信号带宽是无穷宽的。对于这一类函数，我们常定义过零点带宽，因此图6中信号的第一过零点带宽为 $\frac{1}{\tau}$。
  我们再来看另外一种脉冲信号，三角形脉冲波形，如图7所示。写成表达式为
$A\Lambda(\frac{t}{\tau})\quad \leftrightarrow \quad A{\rm Sa}^2\left(\pi f\tau \right).$其中 $\Lambda(\frac{t-t_0}{\tau})$表示底边宽度为 $2\tau$，底边中点在 $t_0$处的三角形脉冲。它的频谱密度函数为Sa函数的平方，第一过零点带宽为 $\frac{1}{\tau}$。

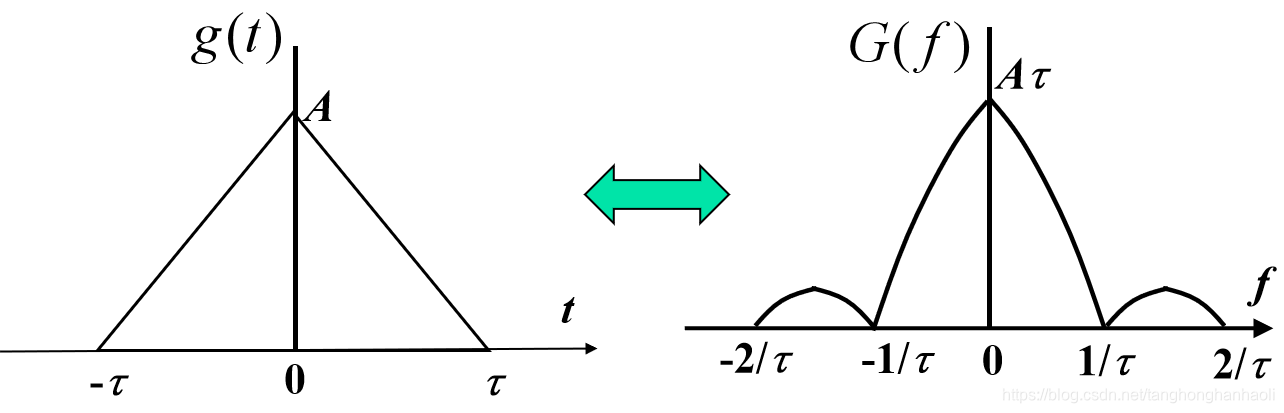
图7 三角形脉冲信号及其频谱密度函数示意图

6、理想低通信号波形与频谱

  理想低通信号，是指其频谱密度函数具有图8(b)中频谱密度的信号，因此其波形具有图8(a)中的形状，表达式为
$g(t)=f_0{\rm Sa}(\pi f_0t)\quad \leftrightarrow \quad G(f)={\rm Rect}\left(\frac{f}{f_0}\right).$因此，理想低通信号就是频谱为矩形函数的信号，根据傅里叶变换的对偶形式，显然波形为Sa函数。注意此时波形的过零点为 $\frac{k}{f_0}$，这里 $k$为不等于零的整数。

提示：矩形脉冲信号与理想低通信号，是两种完全不同的信号。后面也会经常用到这两种波形，大家一定要分清楚二者的区别。

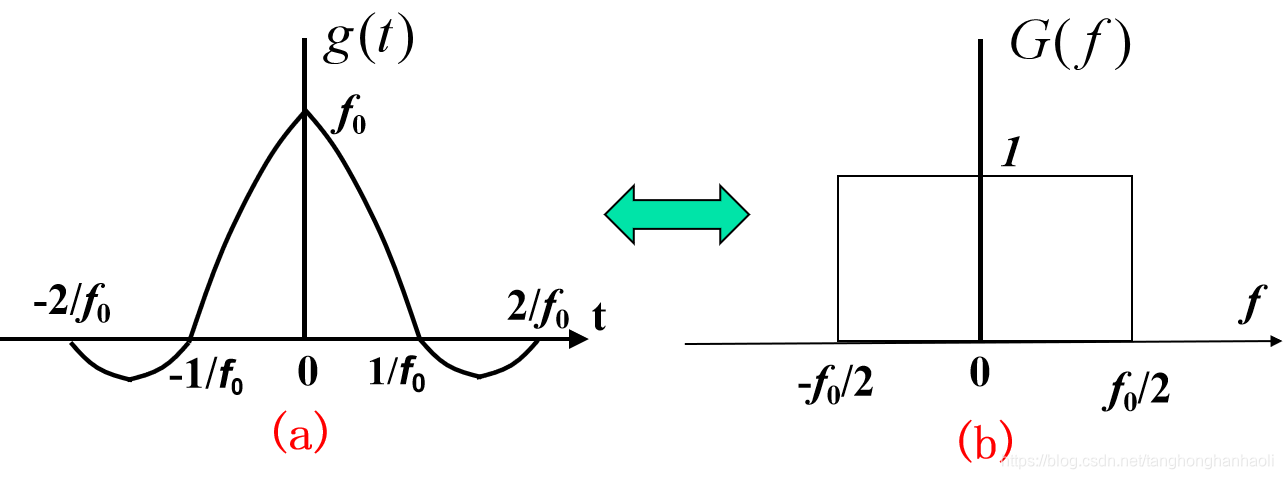
图8 理想低通信号波形与频谱密度函数示意图

7、周期信号的频谱

7.1 周期信号傅里叶变换的一般形式

  周期信号给 $g(t)$傅里叶变换的一般形式为
$\tag{7-1} g(t)\quad \leftrightarrow \quad G(f)=\sum_{k=-\infty}^{\infty}C_n\delta(f-kf_0),$其中 $T_0$为 $g(t)$的周期， $f_0=\frac{1}{T_0}$，
$\tag{7-2} C_n=\frac{1}{T_0}\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}g(t)e^{-j2\pi nf_0t}dt$为 $g(t)$傅里叶级数的系数。直接用上式求解 $C_n$往往比较繁琐。下面我们介绍另一种计算方法：
$\tag{7-3} C_n=\frac{1}{T_0}G_0(f)|_{f=nf_0},$其中 $G_0(f)$为 $g_0(t)$的傅里叶变换，而
$\tag{7-4} g_0(t)=\left\{\begin{aligned} g(t), \quad &t\in [-\frac{T_0}{2},\frac{T_0}{2}]\\ 0,\quad &\rm otherwise \end{aligned}\right.$为 $g(t)$的截断函数。
  从(7-4)可以看出，只要是周期信号，频谱一定是离散的冲激序列，两个冲激之间的间隔为 $f_0$。不同的周期信号， $g_0(t)$不同，因而 $C_n$也就不同，因此冲激的强度也就不同。下面我们来具体看两个周期信号的例子。

7.2 周期冲激序列的频谱

  周期冲激序列波形与频谱示意图如图9所示。周期冲激序列的波形表达式可以写作
$g(t)=\sum_{n=-\infty}^{\infty}\delta(t-nT_0),$可以写出它的截断函数为
$g_0(t)=\delta(t),$因此，有 $G_0(f)=1$，由(7-2)可以得到
$C_n=\frac{1}{T_0},\ n=0,\pm1,\pm 2,\ldots$故可以得到傅里叶变换对
$g(t)=\sum_{n=-\infty}^{\infty}\delta(t-nT_0) \quad \leftrightarrow \quad G(f)=\frac{1}{T_0}\sum_{k=-\infty}^{\infty}\delta(f-kf_0).$不难看出， $G(f)$的每个冲激强度是相等的，这是由 $g_0(t)=\delta(t)$决定的。

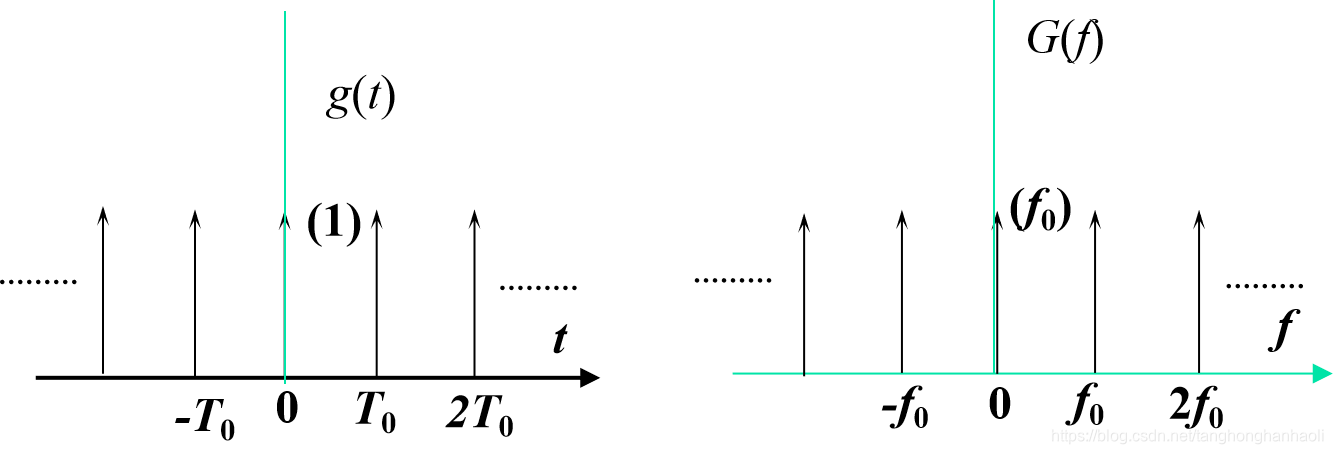
图9 周期冲激序列波形及其频谱密度函数示意图

7.3 周期矩形脉冲序列的频谱

  周期矩形脉冲序列的波形与频谱如图10所示。表达式推导如下：
$\begin{aligned} &g_0(t)={\rm Rect}(\frac{t}{\tau})\quad \leftrightarrow \quad G_0(f)=\tau{\rm Sa}(\pi f\tau) \\ &C_n=\frac{\tau}{T_0}{\rm Sa}(n\pi f_0\tau)\\ &g(t)=\sum_{n=-\infty}^{\infty}{\rm Rect}(\frac{t-nT_0}{\tau}) \quad \leftrightarrow \quad G(f)=\frac{\tau}{T_0}\sum_{k=-\infty}^{\infty}{\rm Sa}(n\pi f_0t)\delta(f-kf_0). \end{aligned}$

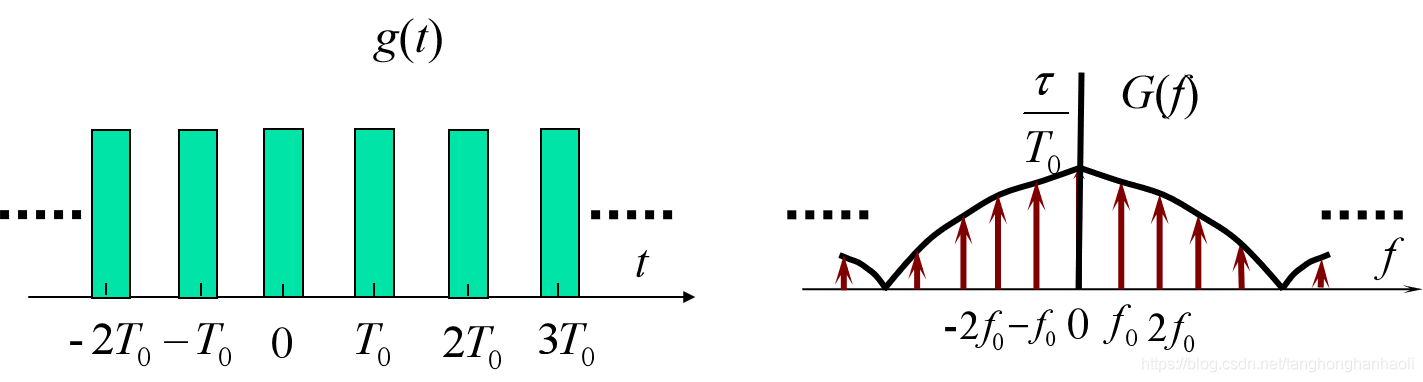
图10 周期矩形脉冲序列波形及其频谱密度函数示意图