摘要:1. 介绍 2.基于归纳法与递归法的设计 3. 更强的假设条件 4.不变式与正确性 5. 松弛法与逐步完善 6. 归简法 + 换位法 = 困难度证明 7. 一些解决问题的建议
本章专注于讨论算法设计的基础技能。本章主题思想 归纳(induction)递归(recursion)及归简(reduction),通常会忽略掉问题的大部分内容,并将讨论聚焦于其解决方案中的某个单一步骤。而最妙的事情在于,该步骤恰是我们所需要的全部,有了它,其余问题迎刃而解。这些解决方案是由密切联系的。某种意义上,归纳法和递归法之间互为镜像,而两者都可以视为归简法的具体示例。
- 归简法指的是将某一问题转化成另一个问题。我们通常都会倾向于将一个未知问题归简成一个已解决的问题。归简法可能会涉及输入(操作中可能会遇到的新问题)与输出(已经解决的原问题)之间的转化。
- 归纳法(或者说数学归纳法)则被用于证明某个语句对于某种大型对象类(通常是一些自然数类型)是否成立。我们首先要证明语句在某一基本情况下(例如当数字为1时)是成立的,然后证明它可以由一个对象“推广到”下一个对象(如果其对于n-1成立,那么它对于n也成立)。
- 递归法则主要被用于函数自我调用时。在这里,我们需要确保函数在遇到基本情况时的操作是正确的,并且能将各层递归调用的结果组合成一个有效的解决方案。
其中,归纳法与递归法都倾向于将问题归简(或分解)成一些更小的子问题,然后探讨出超然于这些问题之外的某一个步骤,并以此来解决整个问题。
1. 介绍
“从某数字列表中找出最邻近但却不相等的两个数字” == “找出某排序序列中最接近的两个数”
棋盘拼接问题 L形砖块
许多所谓的函数式编程语言中都实现有一种被称为尾递归优化的机制。这种优化会修改前面的函数(该函数一般只有最后一句是递归调用),让其不再受递归调用的限制。一般来讲,只需将这些递归调用重写成内部循环。
排序问题的不同实现形式:(任何递归函数都可以重写为相应的迭代操作)
#递归版的插入排序 def ins_sort_rec (seq, i): if i ==0: return ins_sort_rec (seq, i-1) j = i while j >0 and seq[j-1] >seq[j]: seq[j-1], seq[j] = seq[j], seq[j-1] j -= 1 #迭代版的插入排序 def ins_sort (seq): for i in range(1, len(seq)): j = i while j>0 and seq[j-1] > seq[j]: seq[j-i], seq[j] = seq[j], seq[j-1] j -= 1 #递归版的选择排序 def sel_sort_rec(seq, i): if i==0: return max_j = i for j in range(i): if seq[j] > seq[max_j]: max_j = j seq[i], seq[max_j] = seq[max_j], seq[i] sel_sort_rec (seq, i-1) #迭代版的选择排序 def sel_sort(seq): for i in range(len(seq)-1,0,-1): max_j = i for j in range(i): if seq[j] > seq[max_j]: max_j = j seq[i], seq[max_j] = seq[max_j], seq[i]
2.基于归纳法与递归法的设计
2.1 寻找最大排列
在我们尝试设计一个算法之前,往往需要将问题具体化。解决问题最关键的一步是真正的理解他。
#寻找最大排列问题的递归算法思路的朴素实现方案 def naive_max_perm(M, A = none): if A is None: A = set(range(len(M))) if len(A) == 1: return A B = set(M[i] for i in A) C = A - B if C: A.remove(C.pop()) return native_max_perm(M, A) return A
为避免对集合B的重复创建,一种替代方案就是为各元素设置一个计数器。每当有指向X座位的人被淘汰时,就递减该座位的计数器。这种引入计数器的方法非常有用。
#迭代法寻找最大排列问题 def max_perm(M): n = len(M) A = set(range(n)) count = [0]*n for i in M: count[i] += 1 Q = [i for i in A if count[i] ==0] while Q: i = Q.pop() A.remove(i) j = M[i] count[j] -= 1 if count[j] ==0 Q.append(j) return A
2.2 明星问题
该明星不认识人群中的其他人,但是其他人都认识这位明星。换另一种说法,其实就是研究某组依赖关系,寻找一个入手点。核心表现形式就是一个图结构。要寻找一个其他所有节点对它都有入边,但它自身却没有出边的节点。
def celeb(G): n = len(G) u, v = 0, 1 for c in range(2, n+1): if G[u][v]: u = c else: v = c if u== n: c = v else: c = u for v in range(n): if c == v: continue if G[c][v]: break if not G[v][c]: break else: return c return None
#构建一个随机图 from random import randrange n=100 G = [[randrange(2) for i in range(n)] for i in range(n)] #确保其中存在一位明星 c = randrange(n) for i in range(n): G[i][c] = True G[c][i] = False
2.3 拓扑排序问题
几乎所有的项目中,待完成的任务之间都会有某些依赖关系,这些关系会对它们的执行顺序形成部分约束。对于这种依赖关系,将其表示为一个有向非环路图(DAG),并将寻找其中依赖顺序的过程称为拓扑排序。
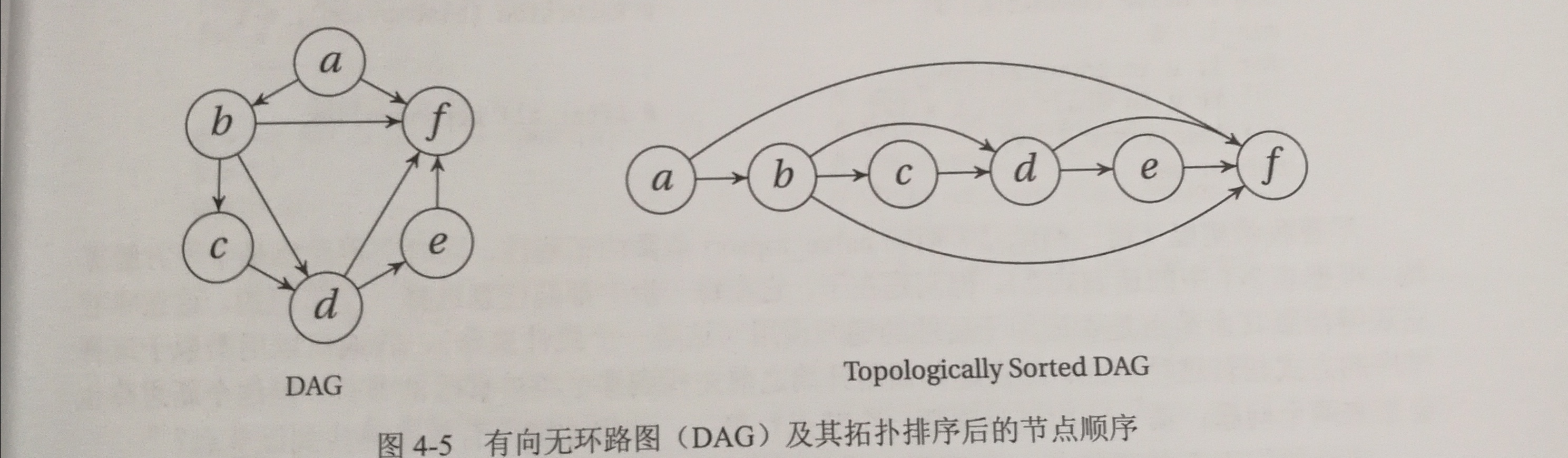
有了DAG后,下一步就是要找到行之有效的归简法。
#有向无环路图的拓扑排序 def topsort(G): count = dict((u, 0) for u in G) for u in G: for v in G[u]: count[v] += 1 Q = [u for u in G if count[u] == 0] S = [] while Q: u = Q.pop() s.append(u) for v in G[u]: count[v] -= 1 if count[v] == 0: Q.append(v) return S
3. 更强的假设条件
默认情况下,我们在设计算法时所设定的归纳前提都是“我们能解决规模更小的问题实例但有时候,这种程度的设定在执行某些实际归纳步骤时是不够用的,或者至少其在执行效率上不够好的。虽然选择子问题的顺序的确很重要(如在拓扑排序算法中),但有时候我们还是必须根据实际情况设置一些更强的假设条件,顺势在我们的归纳操作引入一些额外信息。尽管更强的假设好像会让相关证明变得更加困难,但其实这让我们在进行从n-1(或n/2以及其他规模值)到n的推导工作时有了更多的选择。
4.不变式与正确性
本章的重点是算法设计,因此这里通常关注的是设计过程的正确性。但或许计算机科学在归纳法上还有一种更为常见的观点,我们称之为正确性证明( correctness proofs)该观点内容与本章所讨论的基本相同,但在方法角度上略有不同。当一个完整算法摆在您面前时,往往就需要证明该算法是可以工作的。对于一个递归算法来说,我们已经证明了其思路的直接可用性。但对于一个循环来说,尽管我们也可以用递归思维来思考,但还有一种更适合直接用于迭代操作的归纳法证明的概念,即循环不变式(loop invariants)所谓的循环不变式,实际上是指我们为确保某些事情对于循环中每次迭代操作都成立而设的一些前提条件(之所以叫作不变式,是因为它在相关操作中自始至终都是成立的)。
通常情况下,其最终解决方案就是最后一轮迭代操作后,该循环不变式所达到的那个特定情况,所以如果我们能让该不变式能始终维持下去(以算法的前置条件作为前提),并且证明该循环存在终止状态,那么我们就已经证明了这个算法的正确性。下面我们在插入排序(见清单4-2)中试试这个方法吧。该循环的不变式是元素0到 i 之间是已排序状态(正如代码第一行注释中所提示的那样)。如果我们想用该不变式来证明其正确性,就必须完成以下步骤。
(1)用归纳法证明其在每次迭代操作之后都实际成立。
(2)证明我们将会在该算法终止时得到正确答案。
(3)证明该算法存在终止状态。
在步骤1中,归纳法要证明的内容涉及其基本情况(首轮迭代操作之前的情况)以及相关的归纳步骤(单轮循环中所存在的不变式)。而到了步骤2中,我们涉及的是不变式在循环终止点上的情况。步骤3则往往是最容易被证明的一步(或许您也可以来证明相关事物最终会被“耗尽”)。
其中,步骤2和3在插入排序中应该是显而易见的。首先,该算法的for循环显然会在n轮迭代之后终止(且i=n-1)。其次,该循环的不变式也明显是指元素0到n-1之间始终保持的已排序状态。这意味着问题实际上已经解决了。因为其基本情况(i=0)是显而易见的,所以这里就只剩下归纳步骤了一通过描述如何正确地将下一个元素插入到已排序部分中(不打乱已有排序)的过程来证明循环不变式的存在。
5. 松弛法与逐步完善
松弛法,通过逐步接近的方式获得相关问题的最佳解法。(最短路径算法等基于动态规划的问题,查找最大流量的算法问题......)
提示:用松弛法来进行算法设计就像在玩一种游戏,每运用一次松弛法就好像我们“移动”了一次,而我们要做的就是在尽可能少的移动次数内找到最佳解决方案。从理论上来说,我们可以在整个空间上运用相关的松弛法,但关键在于要找到一个正确的执行顺序。对于这种设计思路,我们将会在处理DAG的最短路径问题(第8章)、 Bellman--ford算法以及 Dijkstra算法(第9章)时进行更深入的探讨。
6. 归简法 + 换位法 = 困难度证明
- 如果我们能将A归简为B,那么B的困难度不会低于A
- 如果我们想通过已知难题A证明X是个难题,那就应该讲Y归简为X
7. 一些解决问题的建议
- 确保自己真正理解了相关问题。这里包括输入什么、输出什么、两者之间是什么关系。然后试着用您所熟悉的数据结构(如某种序列或图结构)来表示该问题实例。此外,有时候先直接提出一个简单粗暴的解决方案也有助于您理清问题的实质内容。
- 找到一种归简方法。这里包括:您是否能将相关输入转换成另一个已解决问题的输入?以及能让其输出结果为己所用?您能否将某个问题实例的规模由n归简至k(k<n),并在展开递归解决方案时将其反推回 n?
- 看看是否有额外的假设条件可用。例如,在一定取值范围内的整数排序比任意值的排序操作更有效率,在某个DAG中寻找最短路径比在任意图结构中找要容易,以及处理非负加权边也通常比任意加权边要简单。