1. 递归
1 递归的定义
- 子程序(或函数)直接调用自己或通过一系列调用语句间接调用自己,称为递归。
- 递归是一种描述问题和解决问题的基本方法。
递归的基本思想:问题分解
当问题比较大,比较复杂,但如果问题本身不变,数据量很小时很容易解决。大问题可以分解为小问题,每个大问题与小问题之间又具备相似性。当小问题很小,小到能够直接解决,然后用小问题来解大问题。这就是递归方法。
递归的要素:
- 递归边界条件:确定递归到何时终止,也称为递归出口
- 递归模式:大问题是如何分解为小问题的,也称为递归体
2 递归实例
1) 阶乘函数

int fact(int n)
{
if(n == 0)
return 1;
else
return n * fact(n-1);
}求解过程:

递归过程与递归工作栈:
- 递归过程在实现时,需要自己调用自己。
- 层层向下递归,返回次序正好相反。

- 递归算法的效率较低;因为返回次序相反,可用栈或循环的非递归方法来实现递归。
//阶乘函数:循环,非递归
int fact1(int n)
{
if(n == 0)
return 1;
else
{
int f = n;
while(--n >= 1)
f *= n;
return f;
}
}2) Fabonacci 数列求解

int fabonacci(int n)
{
if(n <= 1)
return n;
else
return (fabonacci(n-1)+fabonacci(n-2));
}递归关系只在 return 时递归,是尾递归,可以改为循环语句。
//Fabonacci 数列:循环,非递归
int fabo(int n)
{
int pre, now, next, j;
if(n <= 1)
return n;
else
{
pre = 0;
now = 1;
for(j=2;j<=n;j++)
{
next = pre + now;
pre = now;
now = next;
}
return next;
}
}3) 回文串


bool palindrome(string &s, unsigned h, unsigned t)
{
if(h >= t)
return 1; //空串或长度为1
if(tolower(s[h]) == tolower(s[t]))
return palindrome(s,h+1,t-1);
else
return 0;
}递归关系只在 return 时递归,是尾递归,可以改为循环语句。
//回文串:循环,非递归
bool palin(string &s)
{
int h = 0;
int t = strlen(s)-1;
while(h <= t)
{
if(tolower(s[h]) != tolower(s[t]))
return 0;
h++;
t--;
}
return 1;
}2. 分治递归
1 算法的基本思想
- 将要求解的较大规模的问题分割成 k 个更小规模的子问题。

- 对这 k 个子问题分别求解。如果子问题的规模仍然不够小,则再划分为 k 个子问题,如此递归的进行下去,直到问题规模足够小,很容易求出其解为止。
- 将求出的小规模的问题的解合并为一个更大规模的问题的解,自底向上逐步求出原来问题的解。

2 分治法的适用条件
- 该问题的规模缩小到一定的程度就可以容易的解决。
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
- 利用该问题分解出的子问题的解可以合并为该问题的解(完全合并)。(能否利用分治法完全取决于问题是否具有这条特征,如果具备了前两条特征,而不具备第三条特征,则可以考虑贪心算法或动态规划。)
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。(这条特征涉及到分治法的效率,如果各子问题是不独立的,一般用动态规划较好。)
3 分治法的基本步骤

- 平衡子问题。子问题的规模大致相等时算法的效率最高。
4 分治法的复杂性分析

5 实例
1) 打印 n 个数的全排列
算法思想:

#include <iostream>
using namespace std;
void Swap(int &a, int &b)
{
int x = a;
a = b;
b = x;
}
void PrintPermutation(int a[], int k, int n)
{
if (k == n) //排完n个数则输出
{
for(int i=1;i<=n;++i)
{
cout<<a[i]<<" ";
}
cout<<endl;
return;
}
else
{
for(int i=k;i<=n;++i)
{
Swap(a[k],a[i]);
PrintPermutation(a,k+1,n);
Swap(a[k],a[i]); //类似回溯法,返回到上一步
}
}
}
int main()
{
int *a, len;
cout<<"len:"<<endl;
cin>>len;
a = new int[len+1];
if(!a)
return -1;
for(int i=1;i<=len;i++)
a[i] = i;
PrintPermutation(a,1,len);
system("pause");
return 0;
}- 时间复杂度:O(n!)
2) 棋盘覆盖


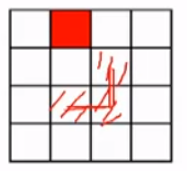
- 时间复杂度:O(n)
3) 买票问题
题目:假设有2n个人买票,票价50元/张,其中有n个人拿50元,n个人拿100元。请问怎么排队,才能够使得卖票处始终有钱找?能够找出所有的有钱找的排队方案吗?