PCA降维笔记

一个非监督的机器学习算法
主要用于数据的降维
通过降维，可以发现更便于人类理解的特征
其他应用：可视化；去噪

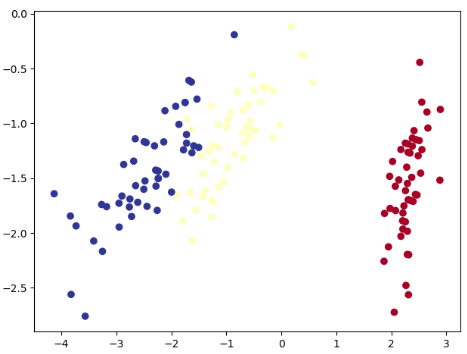
PCA（Principal Component Analysis）是一种常用的数据分析方法。

PCA通过线性变换，将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

降维思路

原数据:

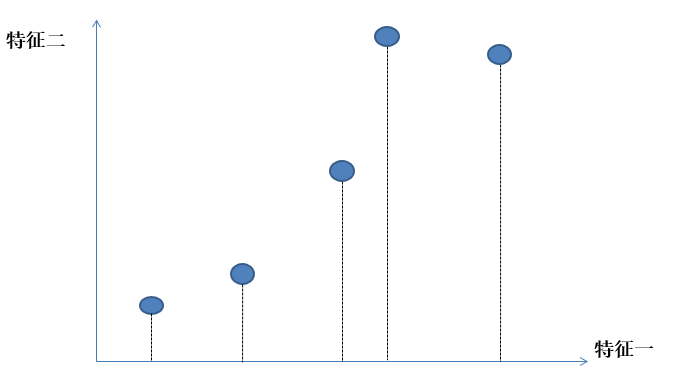
二维数据据降维到一维数:

扫描二维码关注公众号，回复： 6957913 查看本文章

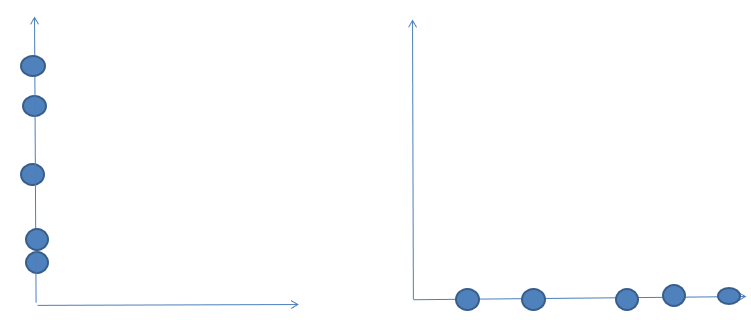
这是去掉特征1和特征2降维后的样子，从图中我们可以感觉到，右边这个比左边这个好一些，因为他们分散的间距比较大，可区分度比较高，这样数据保留的信息也比较多，我们认为这样数据丢失的量就更小一些，达到了我们既降低了维度，又尽可能多保留信息的目的。

如何找到这个让样本间距最大的轴呢？

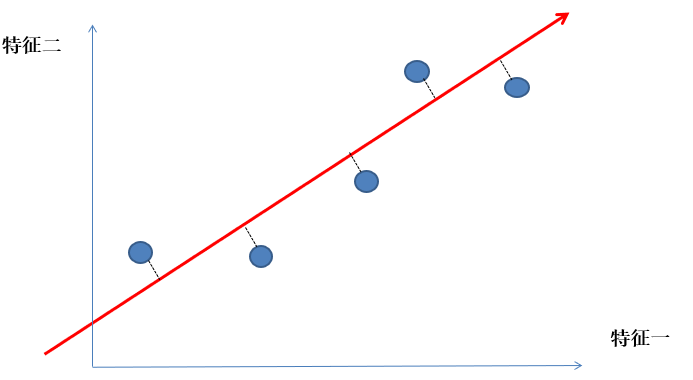
降维推导

随机梯度下降解决降维

第一步将样本均值归零

x = x-x_mean

第二步：求第一主成分的单位向量W=(w1,w2)

我们将所有的样本数据通过投影映射到这个方向向量上得到一个新的向量，我们称作X_pr, 所以我们最后的目标就是为了求方向向量上所有的 X_pr这个向量的方差最大如下图：

第三步:梯度上升来最优化这个方差

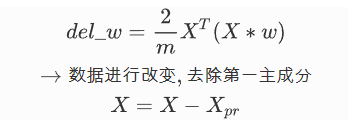
PCA解决降维

降维问题的优化目标

将一组N维向量降为K维（0<K<N），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的K个方差）。

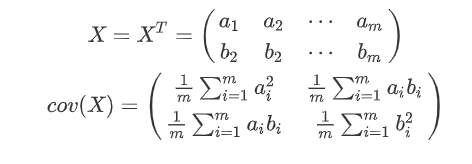
协方差矩阵对角化

前提:

设原始数据矩阵X对应的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据。设Y的协方差矩阵为D，我们推导一下D与C的关系：

现在事情很明白了！我们要找的P不是别的，而是能让原始协方差矩阵C对角化的P。

PCA的算法步骤

设有m条n维数据。

将原始数据X进行转置
将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值
求出协方差矩阵
求出协方差矩阵的特征值及对应的特征向量
将特征向量按对应特征值大小从上到下按行排列成矩阵取前k行组成矩阵P
Y=PX即为降维到k维后的数据

PCA实例

用PCA的方法将整个二维的数据降到一维

1.将原始数据X进行转置

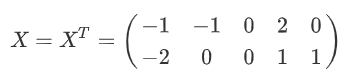
2.将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值

3.求出协方差矩阵

4.求出协方差矩阵的特征值及对应的特征向量

5.将特征向量按对应特征值大小从上到下按行排列成矩阵取前k行组成矩阵P

6.Y=PX即为降维到k维后的数据

这里可以看到D是一个对角化的矩阵,满足的条件

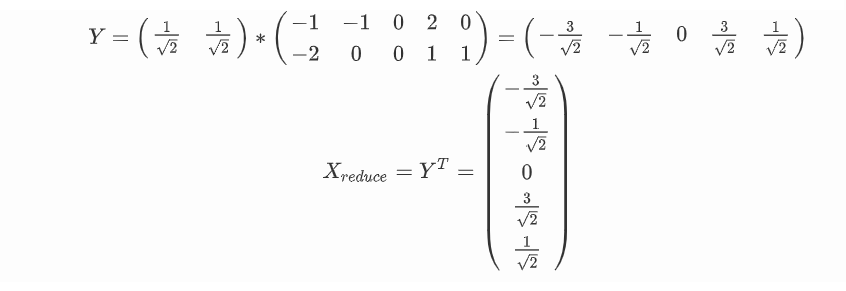
SVD算法解决降维

也就是在PCA的过程中,第三步和第四步改为奇异值分解:

SVD的计算步骤

(1) 对矩阵A和A转置的乘积进行特征值分解

其中v就是右奇异向量.

(2)通过仿真求解左奇异向量

其中奇异值σ跟特征值很类似，在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，其中r<<n，这里定义一下部分奇异值分解:

(3)选择适当的r值,就可以将原数据进行压缩

使用特征值分解实现降维

import numpy as np


def PCA(X, k):
    data = X - np.mean(X, axis=0)
    # 计算协方差矩阵
    cov = np.cov(data.T)
    # 计算协方差矩阵的特征值和特征向量
    eig_val, eig_vec = np.linalg.eig(cov)
    # 将特征值和特征向量组成一个元组
    eig_pairs = [(np.abs(eig_val[i]), eig_vec[:, i]) for i in range(data.shape[1])]
    # 将特征值和特征向量从大到小排序
    eig_pairs.sort(reverse=True)
    # #保留最大的K个特征向量
    ft = []
    for i in range(k):
        ft.append(list(eig_pairs[i][1]))
    return np.dot(data, np.array(ft).T)

使用SVD分解实现降维

def SVD(data, k=2):
    data = data - np.mean(data)
    u, s, vt = np.linalg.svd(data)
    v_reduce = vt[:k, :].T  # 取前k个特征向量
    Z = np.dot(data, v_reduce)
    return Z

梯度上升实现降维

def GD_PCA(X,n_components, eta=0.01, n_iters=1e4):
    # 将均值归零 也就是将坐标轴进行移动
    def demean(X):
        return X - np.mean(X, axis=0)

    # 损失函数(方差)
    def f(w, X):
        return np.sum((X.dot(w) ** 2)) / len(X)

    # 损失函数的导数
    # 把w向量变成单位向量 也就是除于自己的模
    def direction(w):
        return w / np.linalg.norm(w)

    # 进行梯度下降
    def first_component(X, initial_w, eta=0.01, n_iters=1e4, epsilon=1e-8):
        # 保证每次的w为单位向量
        w = direction(initial_w)
        cur_iter = 0
        while cur_iter < n_iters:
            gradient = X.T.dot(X.dot(w)) * 2. / len(X)
            last_w = w
            # 梯度上升
            w = w + eta * gradient
            # 每一次重新迭代前,需要把w向量变成单位向量
            w = direction(w)
            if (abs(f(w, X) - f(last_w, X)) < epsilon):
                break
            cur_iter += 1
        return w

    # 先将整个数据的中心点移动到圆点
    X_pca = demean(X)
    # 分几类就是几行,然后列数就是特征集合的列数
    components_ = np.empty(shape=(n_components, X.shape[1]))
    # 分几类,循环几次
    for i in range(n_components):
        # 此时初始化theta不能为0了
        initial_w = np.random.random(X_pca.shape[1])
        w = first_component(X_pca, initial_w, eta, n_iters)
        components_[i, :] = w
        # 把X_pca在w上的分量去除
        X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
    return X.dot(components_.T)

使用鸢尾花实现降维: