引言：
特征值分解：矩阵的作用就是线性变换（如旋转，伸缩，平移等），在一个空间当中，矩阵左乘向量就是将向量线性变换成想要的效果，那么矩阵的特征值和特征向量是什么呢？
特征值、特征向量：在线性代数的定义当中，特征值和特征向量的定义是这样的，AX=rX ，则称r为A的特征值，X称为A的属于特征值k的特征向量。
这里的矩阵A就是将向量X在空间当中只进行拉伸不进行其他的线性变换，而特征值就是X在空间当中的拉伸的倍数，有些人将它形容成X这个向量的方向上的能量。
矩阵的特征值可以看做这个线性变换的不变的一维子空间，在这个子空间中，方向不变只是能量变化而已。而一些特殊的矩阵就可以全部分为好多个不变的一维子空间，而一般的矩阵除了部分不变的子空间之外还有其他的变换（比如旋转）。通俗来讲就是比如一个二维矩阵作用于一个圆上，理解为一个线性变换，那么该矩阵的特征值在它的特征向量的两个维度上将圆进行拉伸成椭圆，剩下部分就是怎么将圆怎么旋转了。
那么这样做的目的是什么呢？就是讲一个矩阵分解成不同的一维空间，如此就可以将相关研究分别限定在这些子空间中进行，就好比物理中将运动分为竖直运动和水平运动一样更加直观。
矩阵的特征分解与PCA的联系：就是看矩阵在那个一维子空间中所占的特征值最大，若几个相对较大的特征值相加站所有的特征值的绝大部分的话，就代表矩阵在这几个一维子空间当中所含的能量大，则这几个一维子空间就可以约等于这个矩阵了，如此就可以做到降维，在矩阵维度非常大时这起到很大的作用。
奇异值分解：那么特征分解并不是万能的，因为它只能将方阵分解，如果是m*n的矩阵的话就不可以了，这种情况下就要用到奇异值分解了，即A=USVH,这里的U和VH都是正交矩阵（这两个矩阵都相当于旋转），S为对角阵（相当于伸缩），任何矩阵都可以通过一个一个旋转一个伸缩一个旋转得到，这里我是参考博客 矩阵特征值分解与奇异值分解的几何意义的相关知识。那么这里的U，S，V怎么求呢？可以参考维基百科。其中的S就是对角元素为奇异值的对角矩阵，奇异值跟特征值类似，在矩阵A中也是从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前几个大的奇异值来近似描述矩阵A。这里就和前面所说的特征值分解相关了，因为奇异值等于非负的特征值的算术平方根。
一、PCA实现步骤：【换基】【线性】
在PCA中，数据从原来的坐标系转换到新的坐标系，由数据本身决定。转换坐标系时，以方差最大的方向作为坐标轴方向，因为数据的最大方差给出了数据的最重要的信息。第一个新坐标轴选择的是原始数据中方差最大的方法，第二个新坐标轴选择的是与第一个新坐标轴正交且方差次大的方向。重复该过程，重复次数为原始数据的特征维数。
那么，我们如何得到这些包含最大差异性的主成分方向呢？事实上，通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值及特征向量，选择特征值最大（也即包含方差最大）的N个特征所对应的特征向量组成的矩阵，我们就可以将数据矩阵转换到新的空间当中，实现数据特征的降维（N维）。
PCA主要就是实现降维，在一个高维的矩阵当中将其降维这样可以节省好多空间也可以使计算简单，那么PCA是怎么实现的呢？步骤如下：
1.计算观测矩阵的协方差矩阵V：
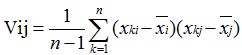
Vij 为原变量Xi与Xj的样本协方差。
2.计算特征值r和特征向量A
解得协方差矩阵的特征值r按大小排列r1>=r2>=r3>=……>=rn>=0,分别求出对应于ri的单位特征向量ai=(ai1,ai2,ai3,……,aip)^T
3.计算PCA的主成分贡献率和累计贡献率
记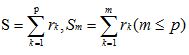
，第i主成分贡献率为ri/S，贡献最大的m个主成分累计贡献率为Sm/S.
一般取达80%~95%的r1,r2,……，rm所对应的主成分。
4.求主成分
Y=AX,其中A为特征向量的矩阵，X为原观察矩阵
二、PCA的物理意义
以上就是PCA的计算步骤，但为什么要这么求呢？
PCA的问题其实是一个基的变换，使得变换后的数据有最大的方差，方差大小代表一个变量所含的信息量，若方差=0的话输入的多个数据就相当于一个数据了，这就没有意义了。
用A Tutorial on Principal Component Analysis论文中的一张图来描述，上面的点为物体运动的轨迹。
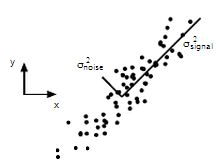
这张图中signal方向上所含的信息较多理应用这个方向来描述物体的运动，但是投影到x,y轴上就不能区分signal这个方向与noise方向上的信息的方差了，为什么呢，因为signal这个方向与x,y轴都成45度，那么这是要将坐标系即基x,y轴转变成signal与noise这两个方向就易分出物体运动轨迹的方差了。
一般方差大的方向就是所含信息最大的方向，PCA当中就是找出一组相互正交的坐标系，第一个轴就是使方差最大的，第二个轴就是与第一个轴正交也使方差最大的，第三个第四个也如此。这样在高维空间中，如果前面m个轴所含的信息量足够大，那么就可以用前m个轴来取代高维，这样可以做到降维并且使得数据压缩损失达到最小。
假设矩阵V的行代表一个样本，列代表一个特征变量（这里很重要，协方差取得是变量之间的方差，而不是样本的），将V进行坐标轴变换，在线性代数课本当中有过将一个基过渡到另外一个基，如X=CY，就是将基Y过渡到X，其中C就是过渡矩阵，那么这里要将原来样本矩阵V过渡到协方差矩阵，这里要把过渡矩阵C求出来也就是上面计算步骤的特征向量A，在求A的同时进行了降维。在图像处理当中，图像可以用像素的灰度形成的矩阵来表示，此时可以用PCA来将图像矩阵来进行压缩，此时就可以将图像一些干扰维度去掉找到图像主成分，使图像更加清晰。
参考的博客：机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用