PCA降维学习笔记与总结

一、简述降维

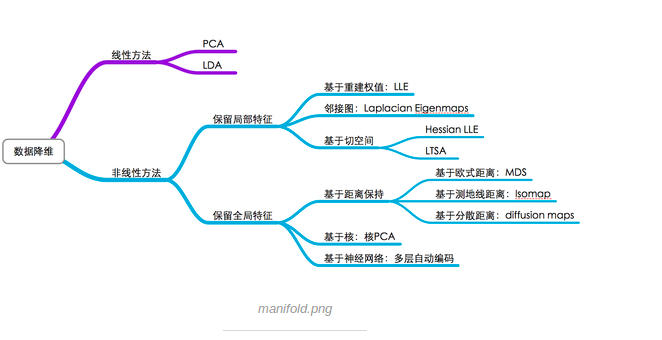
1.1 降维方法的分类

学习PCA笔记，参考的资料：

机器学习之降维方法总结

SVD与PCA

1.2 降维的作用

降低时间复杂度和空间复杂性
节省了提取不必要特征的开销
去掉数据集中夹杂的噪
较简单的模型在小数据集上有更强的鲁棒性
当数据能有较少的特征进行解释，我们可以更好的解释数据，使得我们可以提取知识。
实现数据可视化

二、PCA降维

2.1 概念

主成分分析，Principal components analysis（PCA）是一种分析、简化数据集的技术。PCA的数学定义是：一个正交化线性变换，把数据变换到一个新的坐标系统中，使得这一数据的任何投影的第一大方差在第一个坐标（称为第一主成分）上，第二大方差在第二个坐标（第二主成分）上，依次类推。如下图所示，通过变化将X-Y坐标系映射到signal和noise上：

PCA将维度n进行提炼，降维成k（k<n），数学表达如下：

$A_{m\times n}P_{n\times k}={\widetilde A}_{m\times k}$

其中A矩阵表示m行n维的数据，P表示坐标系的变换。

2.2 原理简介

样本数据：

$\begin{array}{l}Sample:x^{(1)},x^{(2)},\cdots,x^{(m)}\\x^{(1)}=\lbrack x_1^{(1)},x_2^{(1)},x_3^{(1)},\cdots,x_n^{(1)}\rbrack^T\\\end{array}$

降维过程可以看作找到一个或者多个向量u1, u2, ...., un，使得这些向量构成一个新的向量空间（需要学习矩阵分析哦），然后把需要降维的样本映射到这个新的样本空间上。

1.数据归一化：在降维映射的过程中，存在映射误差，所有在对高维特征降维之前，需要做特征归一化（feature normalization）。这个归一化操作包括：(1) feature scaling (让所有的特征拥有相似的尺度，要不然一个特征特别小，一个特征特别大会影响降维的效果) (2) zero mean normalization (零均值归一化)。

Cost Function: $\cos t=\frac1m\sum_{i=1}^m\left\|x^{(i)}-x_{approx}^{(i)}\right\|^2$ ，其中 $x_{approx}^{(i)}$ 表示映射后的坐标

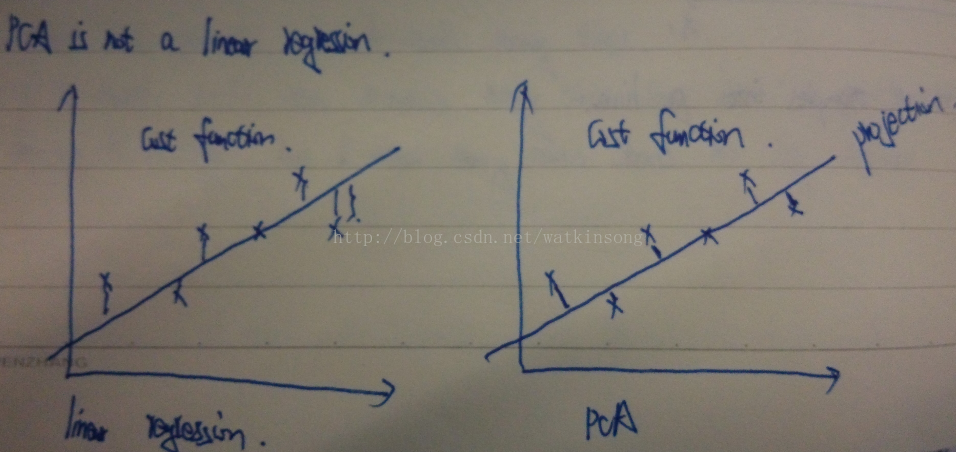
PCA降维和linear regression的Cost Function区别

2.降维矩阵的计算--奇异值分解

(1)特征值：局限于方阵

特征值和特征向量满足： $\begin{array}{l}Av=\lambda v\\\end{array}$

A的特征值分解： $\begin{array}{l}A=Q\Sigma Q^{-1}\\\end{array}$

其中 $\begin{array}{l}Q\\\end{array}$ 是特征向量按照与特征值的对应顺序组合而成 $\begin{array}{l}(v_1,v_2,\dots)\\\end{array}$ ， $\begin{array}{l}\Sigma\\\end{array}$ 是由特征值组成的一个对角矩阵。

(2)奇异值

$\begin{array}{l}A\\\end{array}$ 是一个 $\begin{array}{l}m\times n\\\end{array}$ 的矩阵： $\begin{array}{l}A_{m\times n}=U_{m\times m}\Sigma_{m\times n}V_{n\times n}^T\\\end{array}$

$\begin{array}{l}U\\\end{array}$ 是一个正交矩阵，其向量被称为左奇异向量
$\begin{array}{l}V\\\end{array}$ 是一个正交矩阵，其向量被称为左奇异向量
$\begin{array}{l}\Sigma\\\end{array}$ 是一个 $\begin{array}{l}m\times n\\\end{array}$ 的矩阵，其对角线上的元素为奇异值，其余元素皆为0

(3)特征值与奇异值

求出 $\begin{array}{l}A^TA\\\end{array}$ 的特征值和特征向量， $\begin{array}{l}(A^TA)v_i=\lambda_iv_i\\\end{array}$
奇异值 $\begin{array}{l}\sigma_i=\sqrt{\lambda_i}\\\end{array}$
右奇异向量 $\begin{array}{l}v_i\\\end{array}$
左奇异向量 $\begin{array}{l}\frac1{\sigma_i}Av_i\\\end{array}$

2.3 步骤

给出以下数据集 $D\{(x_1,y_1),\dots,(x_m,y_m)\}$ ，其中 $x\in R^{m\times n}$ ，即原始输出 $DataAdjust_{m\times n}$

分别求 $\overline{x_i}$ ，对于所有样例减去 $\overline{x_i}$ 进行中心化。根据 $\sigma^2=\frac1m{\textstyle\sum_i}(x_j^{(i)})^2$ ，令 $x_j^{(i)}={\textstyle\frac{x_j^{(i)}}\sigma}$ ，进行标准化。
求协方差矩阵 $\Sigma=\frac1m{\textstyle\sum_{i=1}^m}xx^T$ ；
求协方差矩阵对应的特征值和特征向量；
将特征值按照从小到大的顺序排列，选择其中前k个较大值对应的特征向量并组成基矩阵 $EigenVector_{n\times k}$

求最终降维后的矩阵： $FinalData_{m\times k}=DataAdjust_{m\times n}\ast EigenVector_{n\times k}$

三、实验实现部分（模块）

1.数据归一化

import numpy as np
from sklearn.preprocessing import StandardScaler

x = np.array([[10001, 2, 55], [16020, 4, 11], [12008, 6, 33], [13131, 8, 22]])

# feature normalization (feature scaling)
X_scaler = StandardScaler()
x = X_scaler.fit_transform(x)
print(x)

"""
[[-1.2817325  -1.34164079  1.52127766]
 [ 1.48440157 -0.4472136  -1.18321596]
 [-0.35938143  0.4472136   0.16903085]
 [ 0.15671236  1.34164079 -0.50709255]]
"""

2.特征值和特征向量

3.PCA实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#计算均值,要求输入数据为numpy的矩阵格式，行表示样本数，列表示特征
def meanX(dataX):
    return np.mean(dataX,axis=0)#axis=0表示按照列来求均值，如果输入list,则axis=1

"""
参数：
    - XMat：传入的是一个numpy的矩阵格式，行表示样本数，列表示特征    
    - k：表示取前k个特征值对应的特征向量
返回值：
    - finalData：参数一指的是返回的低维矩阵，对应于输入参数二
    - reconData：参数二对应的是移动坐标轴后的矩阵
"""
def pca(XMat, k):
    average = meanX(XMat)
    m, n = np.shape(XMat)
    data_adjust = []
    avgs = np.tile(average, (m, 1))
    data_adjust = XMat - avgs
    covX = np.cov(data_adjust.T)   #计算协方差矩阵
    featValue, featVec=  np.linalg.eig(covX)  #求解协方差矩阵的特征值和特征向量
    index = np.argsort(-featValue) #按照featValue进行从大到小排序
    finalData = []
    if k > n:
        print("k must lower than feature number")
        return
    else:
        #注意特征向量时列向量，而numpy的二维矩阵(数组)a[m][n]中，a[1]表示第1行值
        selectVec = np.matrix(featVec.T[index[:k]]) #所以这里需要进行转置
        finalData = data_adjust * selectVec.T
        reconData = (finalData * selectVec) + average
    return finalData, reconData

"""
finalData(m*k) = data_adjust(m*n) * selectVec(n*k).T
"""

3.PCA函数调用

from sklearn.decomposition import PCA
import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=2)
pca.fit(X)
PCA(copy=True, n_components=2, whiten=False)
print(pca.explained_variance_ratio_)
"""
[0.99244289 0.00755711]
"""

"""
注释
代码编写
    sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)
参数
    n_components: 保留下来的特征个数n
    copy:表示是否在运行算法时，将原始训练数据复制一份
    whiten:白化，使得每个特征具有相同的方差。
PCA对象
    components_：返回具有最大方差的成分
    explained_variance_ratio_：返回所保留的n个成分各自的方差百分比
    n_components_：返回所保留的成分个数n
    mean_：均值
    noise_variance_：方差
函数
    fit(X,y=None)：返回值调用fit方法的对象。比如pca.fit(X)，表示用X对pca这个对象进行训练
    fit_transform(X)：用X来训练PCA模型，同时返回降维后的数据
    inverse_transform()：将降维后的数据转换成原始数据，X=pca.inverse_transform(newX)
    transform(X)：将数据X转换成降维后的数据
"""

PCA降维学习笔记与总结

猜你喜欢