从找规律到组合数学
引入
我们，先来看一道简单的题目：
兔子问题（传送门）
我们这里就不进行累述了。题目呢，你们看看就行。
这是一道经典的题目，让我们思考一下
你是准备用什么方法呢？
找规律？
找规律
重点讲组合数学，本蒟蒻就不再详细讲解找规律了
我们其实可以把每个月的兔子数列出来，就很好找规律了
| 月份 | 兔子数 |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
我们发现后一个月份是前两个月份之和
于是我们就得到一个动态转移公式：
dp[i]=dp[i-1]+dp[i-2];数学归纳法
但是，找规律真的好使吗？
表面来看，可能很爽，但有的题目并不能找到规律（或者规律难找，一时半会儿看不出来）
那么，怎么办?
在我们无从下手的时候，不如再仔细推敲一下，从本质出发。
还是以兔子问题为例，我们再分析一下
兔子问题（传送门）
题目告诉我们，兔子成长有三个阶段，分别是：
int F1;//出生
int F2;//满月（出生后一个月）
int F3;//成年（可以生小兔子）所以，得到以下式子（i为本月月份）：
F1[i]=F3[i-1]+F2[i-1];//上个月成年兔子这个月才会生出小兔子
F2[i]=F1[i-1];//上个月出生的兔子满月了
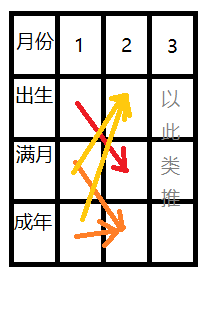
F3[i]=F2[i-1]+F3[i-1];//上个月满月的兔子+上个月已经成年的兔子画图就是这样的：
但这样是不是太复杂了，于是我们就引入了一个 新的概念：
数学归纳法
我们现在定义一个等量关系：
int f[i];//表示本月兔子的总量
f[i]=F1[i]+F2[i]+F3[i];用之前的关系带入后，可表示为：
f[i]=F3[i-1]+F2[i-1]+F1[i-1]+F2[i-1]+F3[i-1];我们发现，正好可以将定义的式子带入，可表示为：
f[i]=f[i-1]+F2[i-1]+F3[i-1];再次展开：
f[i]=f[i-1]+F1[i-2]+F2[i-2]+F3[i-2];最后合并：
f[i]=f[i-1]+f[i-2];是不是有一种设辅助元，然后带入消元的感觉 （误~）
求出多个多种数量的关系式，最后化简成一个单种数量关系，这就是数学归纳法。
题目拓展
走道铺砖（传送门）
也很简单，略过
组合数学中的基本计数原理I
加法原理
大意
加法原理：做一个事有n类办法，第i类办法有f(i)种方法，总的和即为f(1)+f(2)+...+f(i)种方案
详解
加法原理，其实顾名思义，就是加法来解决问题。
例如:
f[i]=f[i-1]+f[i-2];刚刚的兔子问题就是利用加法原理
同类的还有杨辉三角、斐波拉契数列等等，都是加法原理
乘法原理
大意
乘法原理：做一个事分成n个步骤，第i步有f(i)种方法，那么完成这件事共有f(1)f(2)...f(i)种方法
详解
理解乘法原理，我们先来看一个小故事 一个问题
从蒟蒻家到枢纽站有2种方式，从枢纽站到学校有3种方式，问从蒟蒻家到学校，共几种方式？
我们会发现，其实就有2*3=6种方式
刚刚，你在思考这个问题时，其实就涉及到了乘法原理
所谓乘法原理，就是用乘法来解决问题
例如：
f[i]=f[i-1]*f[i-2];在之后的题目中，你也会见到
详细分析排列组合
以下问题都是求方案数
1.n个人分到m个班，每个班人数不限
这个问题，可以分析为：
一个人可以选m个班，有n个人这样选
m* m...m(共n个m)
所以，表示为：m^n
2.n个人排成一列
这和刚才的问题有些类似，但一个位置只能站一个人（也就是说，一个位置只能被一个人选）
那么，第一个人可以有n种站法，第二个人只能有n-1种站法（因为第一个人已经选了一个位置）...
n(n-1) (n-2)...1
所以，表示为：n!
3.n个人中选m个排成一列
我们可以看成站的位置选人，这样就和第二题无较大区别了
也就是：第一个位置可以有n个人来站（也就是n种站法），第二个位置可以有n-1个人来站（就是n-1种站法）...
n(n-1) (n-2)* ...*(n-m+1)
化为表达式，我们将求出所有的排列组合，再除以n-m个并不需要的组合
所以，表示为：n!/(n-m)!
4.n个人中选m个人
所谓选人，那么选出来的人的顺序不同但选的人相同的多种方案看作一种方案
在3的基础上，将求出所有的排列组合，除以n-m个并不需要的组合后,再减去多算的总数
所以，表示为： n !/[(n-m)! * m!]
组合数学中的经典问题
数的划分
题目&理解
题目描述
将整数n分成k份，且每份不能为空，任意两个方案不相同(不考虑顺序)。
例如：n=7，k=3，下面三种分法被认为是相同的。
1，1，5
1，5，1
5，1，1
问有多少种不同的分法。
输入输出格式
输入格式：
n,k (6<n≤200，2≤k≤6)
输出格式：
1个整数，即不同的分法。
输入输出样例
输入样例#1： 复制
7 3
输出样例#1： 复制
4
说明
四种分法为：
1,1,5
1,2,4
1,3,3
2,2,3
这是一道经典的题目，是求方案数
大概意思就是让你求n个数（1-n）分成k份的方案数
暴搜
这不是本章兔子要讲的重点，而且可能会超时，所以不提倡写DFS
但是，因为洛谷的数据太水 所以勉强能过3组
还是放一下程序吧
#include<bits/stdc++.h>
using namespace std;
int n,k,ans;
void DFS(int last,int sum,int cur){
if(cur==k){
if(sum==n)ans++;
return;
}
for(int i=last;i<=n;i++){
DFS(i,sum+i,cur+1);
}
}
int main(){
cin>>n>>k;
DFS(1,0,0);
cout<<ans;
}
正解
分析
用组合数学思维分析：
我们先把k份看成k个抽屉（我们规定!0=1）
1.一号抽屉
- 一号抽屉可以装n-(k-1)个数
PS：n-(k-1)是因为每份都不能为空，(k-1)是除了一号抽屉外，其他抽屉都保证有1个数 - 一号抽屉也可以装n-(k-1)-1个数
PS：也就是比之前的少装1个数，让后面的抽屉多一个数
... ... - 一号抽屉装1个数
PS：让后面的抽屉得到n-1个数
2.二号抽屉
- 二号抽屉类比1号抽屉，二号抽屉每一种方案 + 后面的抽屉需要的数 = 总数 - 一号抽屉获得的数量
PS：因为装法类似，之后三号、四号、五号... ...以此类推
... ... - 一号抽屉装1个数
PS：类比一号抽屉
... ...
n.N号抽屉
- N号抽屉类比一号抽屉
PS：类比，相似
... ... - N号抽屉可以装1个数
PS：保证至少装一个
思路
根据分析，我们发现可以是装抽屉是有状态的，进一步可以推出动态转移方程
设 dp[n,k] 代表将n个小球放到k个盒子中且没有空盒的情况
dp[i][j] = dp[i-1][j-1] + dp[i-j][j]
第一个数为1时+第一个数不为1时
AC代码
所以就很简单啦 ~逃:)
那就贴代码~
#include<bits/stdc++.h>
using namespace std;
int dp[1010][1010];
int n,k;
int main(){
cin>>n>>k;
for(int i=1;i<=n;i++){
dp[i][1]=1;
dp[i][0]=0;
}
for(int i=2;i<=k;i++){
dp[1][i]=0;
dp[0][i]=0;
}
for(int i=2;i<=n;i++){
for(int j=2;j<=k;j++){
if(j>i){
dp[i][j]=0;
}
else{
dp[i][j]=dp[i-1][j-1]+dp[i-j][j];
}
}
}
cout<<dp[n][k];
return 0;
}错排问题
简介
错排问题，是指一个元素可以连向除本身之外的元素连接，每个元素能且只能被其他元素连接一次和只能连接其他元素一次
现在告诉我们元素个数，求方案数
思路
还是可以用搜索，因为太过无脑 ，所以不进行细讲
我们先来看一幅图
感觉就是DP水题
所以根据状态可以得到转移方程
**dp[i] =(i-1)*(dp[i-1]+dp[i-2])**
AC代码
水
#include<bits/stdc++.h>
using namespace std;
int dp[1010];
int n,k;
int main(){
cin>>n;
dp[0]=1;
for(int i=2;i<=n;i++){
dp[i]=(i-1)*dp[i-1]+dp[i-2];
}
cout<<dp[n];
return 0;
}出入栈问题
题目
题目背景
栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作，即pop（从栈顶弹出一个元素）和push（将一个元素进栈）。
栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。
题目描述
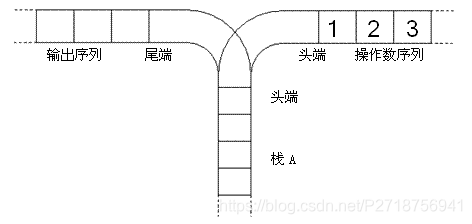
宁宁考虑的是这样一个问题：一个操作数序列，1,2,...,n（图示为1到3的情况），栈A的深度大于n。
现在可以进行两种操作，
1.将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的push操作）
2.将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的pop操作）
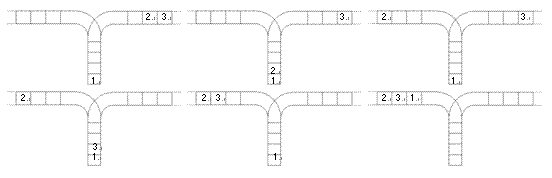
使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由123生成序列231的过程。
（原始状态如上图所示）
你的程序将对给定的n，计算并输出由操作数序列1,2,…,n经过操作可能得到的输出序列的总数。
输入格式
输入文件只含一个整数n(1≤n≤18)
输出格式
输出文件只有1行，即可能输出序列的总数目
输入输出样例
输入 #1
3
输出 #1
5
思路
首先，我们会想到直接用栈来模拟
但是，您超时了，而且不是一般的超时，超时超得有点过分
所以，还是乖乖的写正解DP吧~
x为当前出栈序列的最后一个，则x有n种取值
x是最后一个出栈的，所以将已出栈的东西分成两部分
- 比x小：x-1个，所以这些数的全部出栈可能为dp[x-1]
- 比x大：n-x个，所以这些数的全部出栈可能为dp[n-x]
所以得到动态转移方程：
dp[i]+=dp[i-1] * dp[i-x]
AC代码
#include<bits/stdc++.h>
using namespace std;
int n;
int dp[1010];
int main(){
cin>>n;
dp[0]=1;
dp[1]=1;
for(int i=2;i<=n;i++){
for(int j=0;j<i;j++){
dp[i]+=dp[j]*dp[i-j-1];
}
}
cout<<dp[n];
return 0;
}括号序列问题
题目
题目描述
定义如下规则序列(字符串)：
- 空序列是规则序列；
- 如果S是规则序列，那么(S)和[S]也是规则序列；
- 如果A和B都是规则序列，那么AB也是规则序列。
例如，下面的字符串都是规则序列：
()，[]，(())，([])，()[]，()[()]
而以下几个则不是：
(，[，]，)(，())，([()
现在，给你一些由‘(’，‘)’，‘[’，‘]’构成的序列，你要做的，是补全该括号序列，即扫描一遍原序列，对每一个右括号，找到在它左边最靠近它的左括号匹配，如果没有就放弃。在以这种方式把原序列匹配完成后，把剩下的未匹配的括号补全。
输入格式
输入文件仅一行，全部由‘(’，‘)’，‘]’，‘]’组成，没有其他字符，长度不超过100。
输出格式
输出文件也仅有一行，全部由‘(’，‘)’，‘]’，‘]’组成，没有其他字符，把你补全后的规则序列输出即可。
说明/提示
将前两个左括号补全即可。
理解
这道题题目描述不太清楚，卡了兔子二十多分钟（可能是兔子太过蒟蒻）
然后兔子就WA了七八遍
是某谷的问题
好吧，是过于兔子蒟蒻的问题
题目告诉我们一个括号序列，然后要求我们求它经过补全后的序列。
注意： 补全不是题目中说的最短序列，不是括号嵌套层数最小的序列。
题意是指： 遍历一遍原序列，然后给每一个右括号找它左边最近的左括号，如果没有，就在这种方式把原序列遍历完后，补全剩下未匹配的括号。
思路
我们用栈来存储没有匹配括号的括号
定义一个匹配的数组，用来给没有匹配括号的括号匹配括号
for循环从0到size过一遍
AC代码
#include<bits/stdc++.h>
using namespace std;
int n;
char s[1010],b[1010];
int fh[300];
char tj[9]={'>','}',']',')','0','(','[','}','<'};
stack<int> st;
int main() {
cin>>s;
int l=strlen(s);
fh['(']=-1;
fh[')']=1;
fh['[']=-2;
fh[']']=2;
fh['{']=-3;
fh['}']=3;
fh['<']=-4;
fh['>']=4;
for(int i=0; i<l; i++) {
char c=s[i];
if(fh[c]<0){
st.push(i);
}
else{
if(!st.empty()){
int k=st.top();
if(fh[s[k]]+fh[c]==0){
b[i]=b[k]=1;
st.pop();
}
}
}
}
for(int i=0; i<l; i++){
if(b[i]){
cout<<s[i];
}else{
int k=fh[s[i]];
if(k<0){
cout<<s[i]<<tj[4+k];
}else{
cout<<tj[4+k]<<s[i];
}
}
}
}二叉树计数
题目
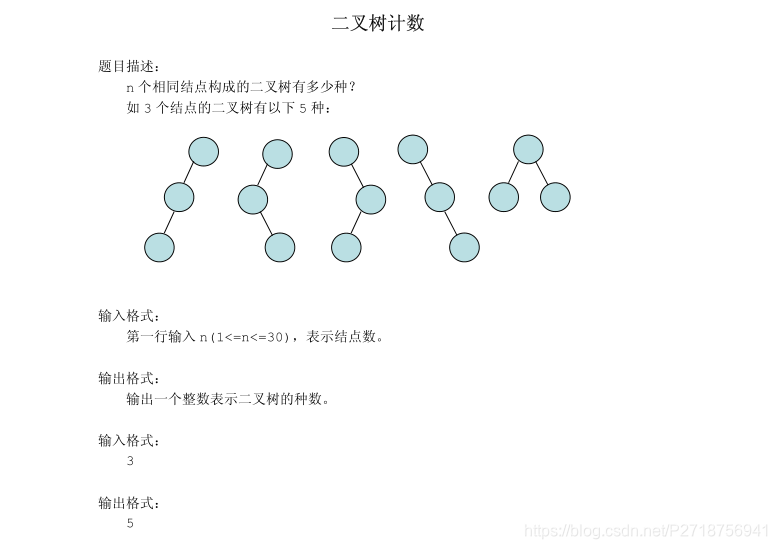
思路
我们只看左右两边。
设一共有i个节点，左边有j个节点，则右边有i-j-1个节点。
设a[i]为方案数，则左边有a[j]种，右边有a[i-j-1]种
总数a[i]=a[j]*a[i-j-1]
AC代码
#include<bits/stdc++.h>
using namespace std;
int dp[10010];
int n;
int main(){
cin>>n;
dp[0]=1;
for(int i=1;i<=n;i++){
for(int j=0;j<=i;j++){
dp[i]+=dp[j]*dp[i-j-1];
}
}
cout<<dp[n];
}凸多边形划分
简介
在一个凸多边形中，通过若干条互不相交的对角线，把这个多边形划分成了若干个三角形。输入凸多边形的边数n，求不同划分的方案数。
思路
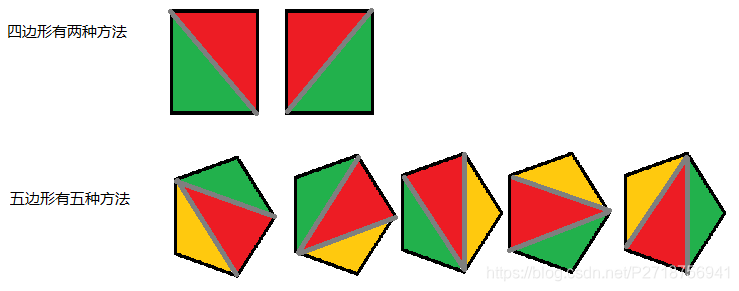我们观察后知道，一个顶点可以延伸出n-2条边
PS：n-2是指：从一个顶点延伸出的边；-2是指：一个顶点不能和相邻的两个顶点相连，这是肯定的，所以需要 -2。
我们现在给每个点编号：
顶点1：可以选择n-2个顶点
顶点2：可以选择n-2-1个顶点（-1因为顶点1选择了一个顶点）
顶点3：可以选择n-2-2个顶点
... ...
顶点n：可以选择1个顶点（前n-1个顶点已连接了n-1个顶点）
我们可以得到动态转移方程：
dp[i]=dp[i]+dp[j] * dp[i-j+1]
AC代码
#include<bits/stdc++.h>
using namespace std;
int dp[10010];
int n;
int main(){
cin>>n;
dp[2]=1;
for(int i=3;i<=n;i++){
for(int j=2;j<i;j++){
dp[i]=dp[i]+dp[j]*dp[i-j+1];
}
}
cout<<dp[n];
}圆排列
简介
我们先来看一个问题：
有一张圆桌，坐了n个人，可以有多少中方案？
对于围成圆圈的n个元素，同时按同一方向旋转，即每个元素都向左(或向右)转动一个位置，虽然元素的绝对位置发生了变化，但相对位置未变，即元素间的相邻关系未变，这样的圆排列认为是同一种，否则便是不同的圆排列
思路
- 先让n个元素任意排成一列，共有n!种排法
- 再让其首尾相接，当每个元素又转动到原先的位置时，相当于n个不同的排列
所以，圆排列的方案数为n!/n（n!为排成一列的排法，/n是除多出的排列）
也可以写成(n-1)!
AC代码
#include<bits/stdc++.h>
using namespace std;
int n;
int x=1;
int main(){
cin>>n;
for(int i=3;i<=n;i++){
x*=(i-1);
}
cout<<x;
}
组合数学中的基本计数原理II
容斥原理
简介
在计数时，我们不希望有重叠后重复记录的现象
容斥原理则可以帮助我们去掉重叠后重复出现的记录
容斥原理：把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去
详解
还是先讲个故事 一道题目：
蒟蒻兔子所在的YC中学搞了社团活动（纯属虚构）
社团有：
信息学社团、机器人社团、网页制作社团
信息学有14人，机器人有20人，网页制作有12人
其中，机器人社团有2人加入了信息学社团，网页制作社团也有4人在信息学社团中，还有1人参加了网页制作和机器人社团，还有2人参加了所有社团
求一共有多少人加入社团活动
题目很乱，我们可以整理成一幅图就可以清楚了：
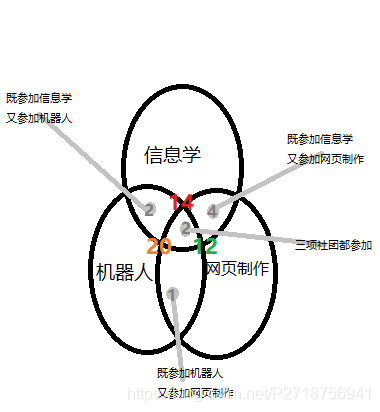
很像容斥原理
其实，遇到容斥原理，我们都可以画图解析
用容斥原理来做，我们不得不提到一个流程
容斥原理流程：
- 不考虑重叠的情况，进行计算
- 将计数时重复计算的数目减去
容斥原理公式
A类和B类和C类元素个数总和=A类元素个数+ B类元素个数+C类元素个数-既是A类又是B类的元素个数-既是A类又是C类的元素个数-既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。
现在一个可以做了吧
答案是：14+20+12-2-1-4+2=21(人)
抽屉原理
简介
m个集合，放n个元素。
详解
其实就是排列组合
我们可以看做是有m个抽屉，放n个苹果
我们可以怎么放呢？
求排列组合的方案，这就是抽屉原理的思想
其实，我们小学就在奥数中学过：
原理1. 把多于n+1个的物体放到n个抽屉里，则至少有一个抽屉里的东西不少于两件。
原理2. 把多于mn(m乘n)+1（n不为0）个的物体放到n个抽屉里，则至少有一个抽屉里有不少于（m+1）的物体。
原理3. 把无穷多件物体放入n个抽屉，则至少有一个抽屉里有无穷个物体。
原理4. 把（mn－1）个物体放入n个抽屉中，其中必有一个抽屉中至多有（m—1）个物体(例如，将3×5-1=14个物体放入5个抽屉中，则必定有一个抽屉中的物体数少于等于3-1=2)。
也挺简单的，看看就行了~
总结
组合数学是一种思想，可能有些抽象（也许是兔子太蒟蒻了吧），但如果理解之后，便会成为解题的一把利器。
本章基本没有提到代码，因为组合数学对思维的要求大于代码量，所以重点放在了思维的讲解上。
其实，蒟蒻的兔子到现在也是有点晕，如果本章讲的有什么不对的地方，请大佬指教