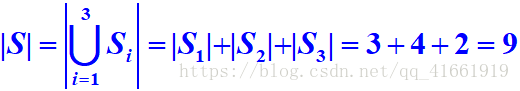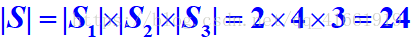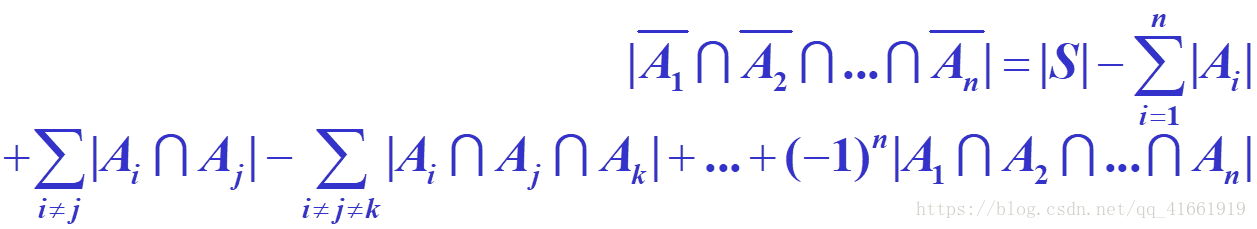组合数学总结

前言：虽然书上的基本知识都看完了，也看懂了，但是对于课本上这一部分的例题，感觉难度还是不小的，可能是自己对于基本知识的理解还不到位，感觉自己可以先做一部分模板题，熟悉一下这些知识，然后再逐渐提升。

一、基础知识梳理：

1、计数原理：加法原理，乘法原理，鸽巢原理、容斥原理；

①加法原理：即A∪B，（注意A、B之间是互斥的，交集为空集）：

例1、有一所学校给一名物理竞赛优胜者发奖，奖品有三类，第一类是三种不同版本的法汉词典；第二类是四种不同类型的物理参考书；第三类是二种不同的奖杯。这位优胜者只能挑选一样奖品。那么，这位优胜者挑选奖品的方法有多少种？

解：设S是所有这些奖品的集合，Si是第i类奖品的集合(i=1,2,3)，显然，Si∩Sj=Φ (i≠j) ，根据加法法则有

②乘法原理：即A∩B（A、B之间是相互独立的)：

例2、从A 地到B地有二条不同的道路，从B地到C地有四条不同的道路，而从C地到D地有三条不同的道路。求从A地经B、C两地到达D地的道路数。

解：设S是所求的道路数集合，S1、S2、S3分别是从A到B、从B到C、从C到D的道路集合，根据乘法法则有

③鸽巢原理，又称抽屉原理：

即将n+1个物体放入n个盒子中，则必然至少有一个盒子中放入>=2件的物体。

例3、一个教师每周上7次课，则这教师至少有一天要上至少2次课（星期天不上课除外）。

证明：此例中把“天”当作盒子，

相当于6个盒子放7个物体，从而得证。（注意：鸽笼原理只能说明至少存在这么一个盒子，但具体是哪一个盒子并不能确定）。

④容斥原理：

首先，我们要知道这么几个公式及定理：

1*：DeMorgan定律：设A、B为全集U的两个子集，则有： $\overline{A\cup B}=\overline{A}\cap \overline{B}$ ，以及 $\overline{A\cap B}= \overline{A}\cup\overline{B}$ ；

定理2： $\left |\overline{A}\cap \overline {B} \right |=\left |S \right |-\left |A \right |-\left |B \right |+\left |A\cap B \right |$

由上述两式可以推广到n件事件的情况。

3*容斥定理：

$若Ai (i=1,2,…,n) S，且Ai是S中具有性质pi的元素的子集，则S中不具有性质pi (i=1,2,…,n)的元素的个数为：$ Ai (i=1,2,…,n) ∈S，且Ai是S中具有性质pi的元素的子集，则S中不具有性质pi (i=1,2,…,n)的元素的个数为：

对应容斥原理的一部分练习题：https://blog.csdn.net/qq_41661919/article/details/81352650

2、婚姻配对问题（G-S算法）：

其原理大概是：男的依次向自己喜欢的女生表白，如果女生还没有男友或者该男生比女生的现男友优秀，则表白成功，反之，表白失败，在下一轮中再向其它女生表白，如此循环，直至所有男生与女生配对。难点在于信息的记录与存储上。

其次对于该问题主要就是模板的应用了。。。POJ3487\HDU1522。

3、组合问题分类：存在、计数、构造、最优。（找规律\递推）

4、排列：

①：n个元素中可重复的选出m个元素的排列，排列方案数： $n^{m}$ 。

②：n个元素中有 $n_{1}$ 个相同元素， $n_{2}$ 个相同元素...... $n_{m}$ 个相同元素，且 $n_{1}+n_{2}+......+n_{m}=n$ ，则n个元素中取r各元素的选排列方案总数为 $\frac{A_{n} ^{r}}{n_{1}!*n_{2}!*...*n_{m}!}$ 。