C++高级数据结构算法 | 动态规划（Dynamic Programming）

文章目录

从斐波那契数列谈起
动态规划的基本概念
动态规划的基本思想
动态规划经典题目分析

钢条切割问题
硬币问题
最大子段和问题
最长递增子序列（LIS）
最长公共子序列（LCS）
0-1背包问题

从斐波那契数列谈起

首先先来谈谈我们非常熟悉的斐波那契数列：

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（LeonardodaFibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……n。在数学上，斐波纳契数列以如下被以递推的方法定义：F(1)=1，F(2)=1,F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）。

问题描述很清楚，并且给出了递推式，那么我们可以很简单的实现一个递归版本：

int Fibonacci(int n)
{
	if(n <= 0)
		return 0;
		
	if (n == 1 || n == 2)
		return 1;

	return Fibonacci(n - 1) + Fibonacci(n - 2);
}

接下来我们分析一下上述程序的执行效率，如下图所示：

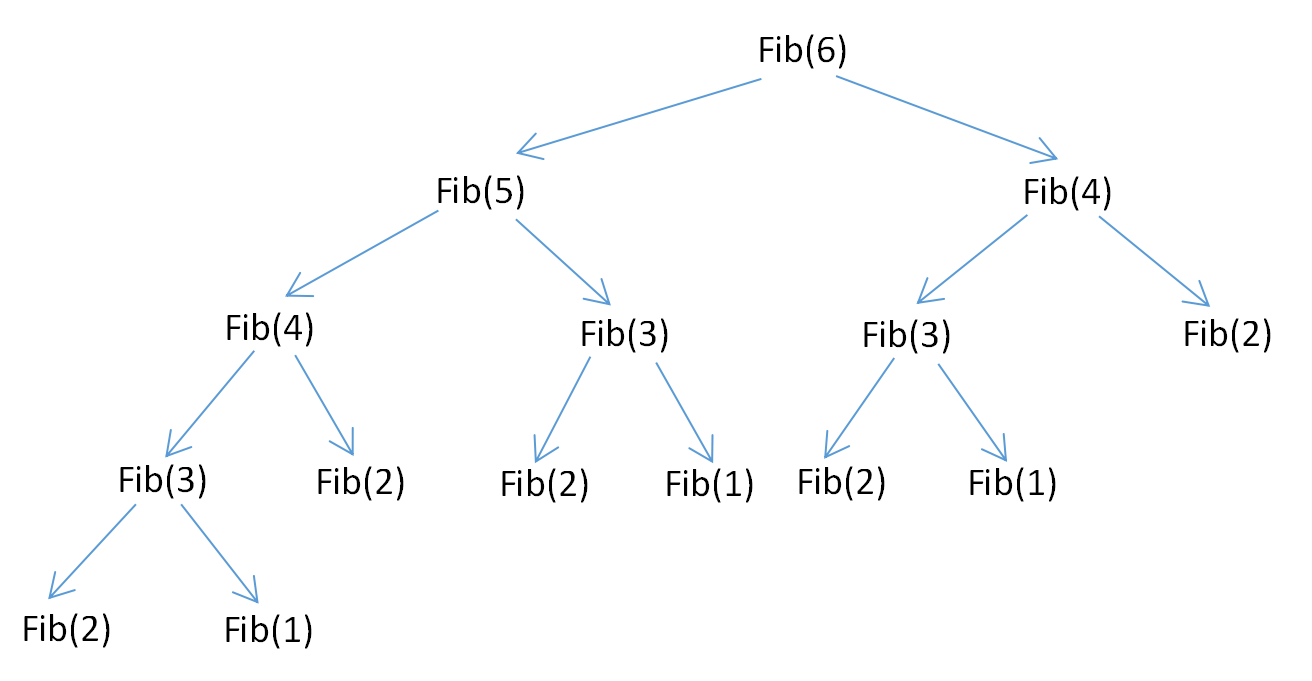
上面的递归树中的每一个子节点都会执行一次，很多重复的节点被执行，Fib(2)被重复执行了5次。由于调用每一个函数的时候都要保留上下文，所以空间上开销也不小。

那么我们试想一下：如果在执行的时候把执行过的子节点保存起来，后面要用到的时候直接查表调用的话可以节约大量的时间。改进的程序如下。

int Fibonacci(int n)
{
	if (n <= 0)
		return -1;
	
	/* 使用dp数组来保存已求过的值 */
	int* dp = new int[n + 1];
	for (int i = 0; i <= n; ++i)
	{
		dp[i] = -1;
	}

	return Fibonacci(dp, n);
}

int Fibonacci(int dp[], int n)
{
	/* dp[n]已经被记录，直接返回其值，不再重复计算 */
	if (dp[n] != -1)
		return dp[n];

	if (n <= 2)
	{
		dp[n] = 1;
	}
	else
	{
		dp[n] = Fibonacci(dp, n - 1) + Fibonacci(dp, n - 2);
	}

	return dp[n];
}

上述程序中我们使用的就是动态规划的思想，记录已求过的解，不去重复计算子问题，上述方法称为自顶向下的备忘录法 。

备忘录法是比较好理解的，创建了一个 $n+1$ 大小的数组来保存求出的斐波拉契数列中的每一个值，在递归的时候如果发现前面的值 $dp[n]$ 计算出来了就不再计算，提高了算法的效率，避免了很多冗余的计算。

但是备忘录法的动态规划仍然是基于递归实现的，不管怎样，计算 $dp[6]$ 的时候最后还是要计算出 $dp[1]、dp[2]、dp[3]···$ ，那么何不先计算出 $dp[1]、dp[2]、dp[3]···$ 呢？这也就是动态规划的核心，先计算子问题，再由子问题计算父问题。

接下来我们看一下使用自底向上的动态规划如何解决斐波那契数列：

int Fibonacci(int n)
{
	int* dp = new int[n + 1];

	dp[0] = 1;
	dp[1] = 1;
	for (int i = 2; i < n; i++)
	{
		dp[i] = dp[i - 1] + dp[i - 2];
	}
	return dp[n - 1];
}

自底向上方法也是利用数组保存了先计算的值，为后面的调用服务。

我们观察发现参与循环的只有 $i，i-1， i-2$ 三项，即父问题的解只依赖于之前的两个子问题，因此我们直接使用变量更新即可，进一步的压缩如下：

int Fibonacci(int n)
{
	if (n <= 0)
		return -1;

	int first = 1;
	int second = 1;
	int result = 1;
	for (int i = 2; i < n; i++)
	{
		first = second;
		second = result;
		result = first + second;
	}
	return result;
}

动态规划的基本概念

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。

1、多阶段决策问题

如果一类活动过程可以分为若干个互相联系的阶段，在每一个阶段都需作出决策(采取措施)，一个阶段的决策确定以后，常常影响到下一个阶段的决策，从而就完全确定了一个过程的活动路线，则称它为多阶段决策问题。

各个阶段的决策构成一个决策序列，称为一个策略。每一个阶段都有若干个决策可供选择，因而就有许多策略供我们选取，对应于一个策略可以确定活动的效果，这个效果可以用数量来确定。策略不同，效果也不同，多阶段决策问题就是要在可以选择的那些策略中间，选取一个最优策略，使在预定的标准下达到最好的效果。

2、动态规划问题中的术语

阶段：把所给求解问题的过程恰当地分成若干个相互联系的阶段，以便于求解，过程不同，阶段数就可能不同．描述阶段的变量称为阶段变量。

状态：状态表示每个阶段开始面临的自然状况或客观条件，它不以人们的主观意志为转移，也称为不可控因素。

无后效性：无后效性指如果在某个阶段上过程的状态已知，则从此阶段以后过程的发展变化仅与此阶段的状态有关，而与过程在此阶段以前的阶段所经历过的状态无关。

决策：给定一个状态，从该状态演变到下一个阶段的某个状态的一种选择成为决策。决策可表示为一个数或一组数，不同的决策对应不同的数值。因为满足无后效性，每个阶段选择决策时只需考虑当前的状态无需考虑历史状态。

策略：由每个阶段的决策组成的序列称为策略。

状态转移方程：给定 $k$ 阶段状态变量 $x(k)$ ，若 $k+1$ 阶段状态变量 $x(k+1)$ 也确定下来，这就是状态转移的规律，称为状态转移方程。

基本模型：

确定问题的决策对象。
对决策过程划分阶段。
对各阶段确定态变量。
根据状态变量确定费用函数和目标函数。
建立各阶段状态变量的转移过程，确定状态转移方程。

动态规划的基本思想

动态规划程序设计是对解最优化问题的一种途径、一种方法，而不是一种特殊算法。不像搜索或数值计算那样，具有一个标准的数学表达式和明确清晰的解题方法。动态规划程序设计往往是针对一种最优化问题，由于各种问题的性质不同，确定最优解的条件也互不相同，因而动态规划的设计方法对不同的问题，有各具特色的解题方法，而不存在一种万能的动态规划算法，可以解决各类最优化问题。

动态规划（ dynamic programming ）是解决多阶段决策过程最优化问题的一种常用方法。利用动态规划算法，可以优雅而高效地解决很多贪婪算法或分治算法不能解决的问题。

动态规划算法的基本思想是：将待求解的问题分解成若干个相互联系的子问题，先求解子问题，然后从这些子问题的解得到原问题的解；对于重复出现的子问题，只在第一次遇到的时候对它进行求解，并把答案保存起来，让以后再次遇到时直接引用答案，不必重新求解。

动态规划算法将问题的解决方案视为一系列决策的结果，与贪婪算法不同的是，在贪婪算法中，每采用一次贪婪准则，便做出一个不可撤回的决策；而在动态规划算法中，还要考察每个最优决策序列中是否包含一个最优决策子序列，即问题是否具有最优子结构性质。

动态规划算法的有效性依赖于待求解问题本身具有的两个重要性质：

最优子结构性质
子问题重叠性质

最优子结构性质：如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。

子问题重叠性质：子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的算法效率。

当我们已经确定待解决的问题需要用动态规划算法求解时，通常可以按照以下步骤设计动态规划算法：

$1、$ 分析问题的最优解，找出最优解的性质，并刻画其结构特征；
$2、$ 递归地定义最优值；
$3、$ 采用自底向上的方式计算问题的最优值；
$4、$ 根据计算最优值时得到的信息，构造最优解。

1 ～ 3 步是动态规划算法解决问题的基本步骤，在只需要计算最优值的问题中，完成这三个基本步骤就可以了。如果问题需要构造最优解，还要执行第 4 步；此时，在第 3 步通常需要记录更多的信息，以便在步骤 4 中，有足够的信息快速地构造出最优解。

动态规划其实质上是通过开辟记录表，记录已求解过的结果，当再次需要求解的时候，可以直接到那个记录表中去查找，从而避免重复计算子问题来达到降低时间复杂度的效果。实际上是一个空间换时间的算法。动态规划，通常可以把指数级的复杂度降低到多项式级别。

来自知乎的文章，对 “阶段”、“状态”的概念讲的非常清楚：《什么是动态规划（Dynamic Programming）？动态规划的意义是什么？》

文章最后给出了不同算法的特征：

每个阶段只有一个状态 $→$ 递推；
每个阶段的最优状态都是由上一个阶段的最优状态得到的 $→$ 贪心；
每个阶段的最优状态是由之前所有阶段的状态的组合得到的 $→$ 搜索；
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到而不管之前这个状态是如何得到的 $→$ 动态规划。

每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到，这个性质叫做最优子结构；而不管之前这个状态是如何得到的这个性质叫做无后效性。

其实动态规划中的最优状态的说法容易产生误导，以为只需要计算最优状态就好，LIS问题确实如此，转移时只用到了每个阶段“选”的状态。但实际上有的问题往往需要对每个阶段的所有状态都算出一个最优值，然后根据这些最优值再来找最优状态。比如背包问题就需要对前 i 个包（阶段）容量为 j 时（状态）计算出最大价值。然后在最后一个阶段中的所有状态种找到最优值。

动态规划经典题目分析

钢条切割问题

这是一道来自《算法导论》的经典例题：

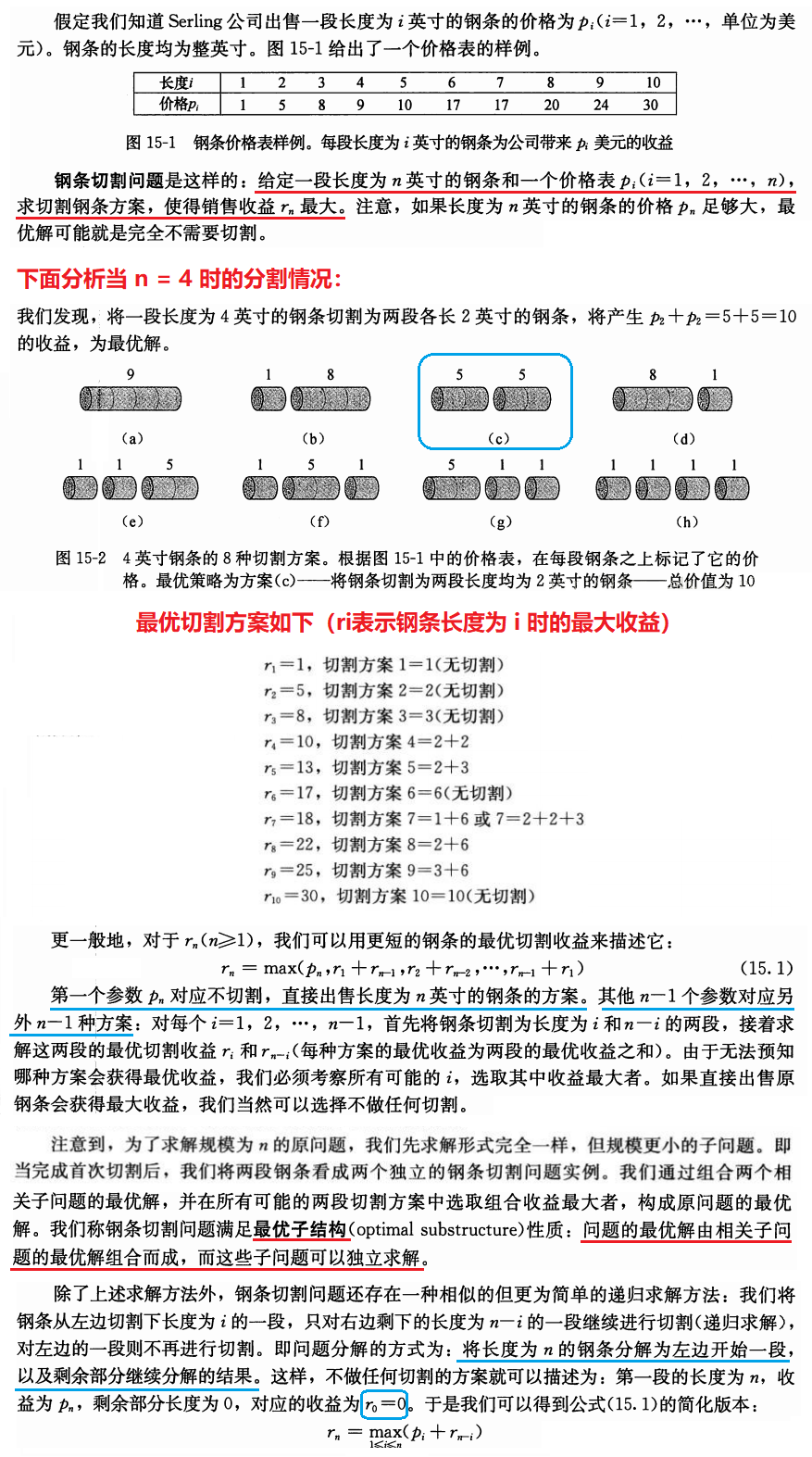
接下来我们使用一下前面讲到三种方法来实现一下钢条切割。

朴素递归算法

int cutRod(int p[], int n)
{
	if (n == 0)
		return 0;

	int q = INT8_MIN;

	for (int i = 1; i <= n; ++i)
	{
		q = max(q, p[i] + cutRod(p, n - i));
	}

	return q;
}

递归很好理解，递归的思路其实和回溯法是一样的：遍历所有解空间，但这里和上面斐波拉契数列的不同之处在于，在每一层上都进行了一次最优解的选择:

$q = max(q, p[i] + cutRod(p, n - i));$

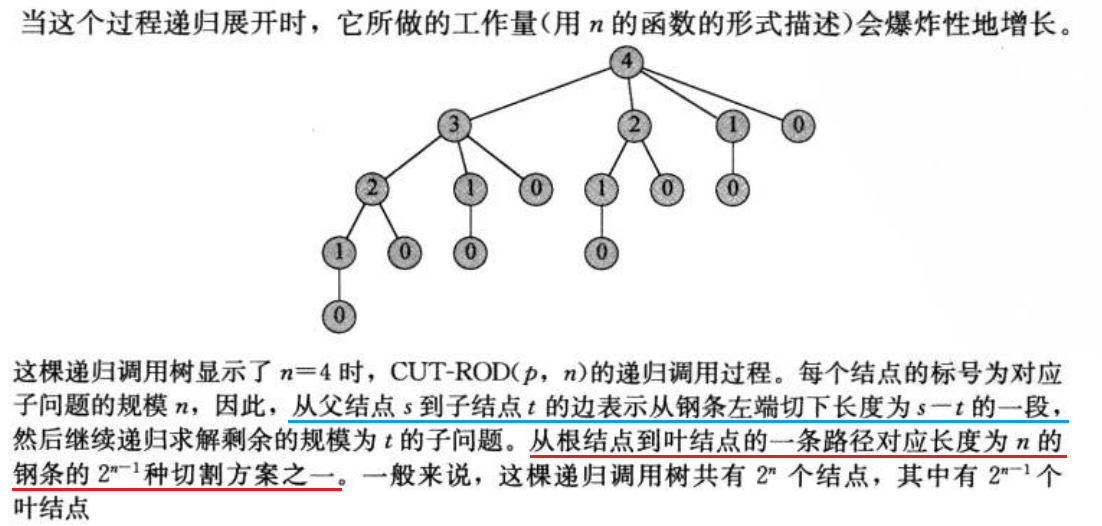
我们通过上面的分析得出，程序存在子问题重叠，进行了多次求解，算法效率是非常低的，那么接下来我们使用动态规划方法求解钢条切割的最优化问题。

1、带备忘的自顶向下法

int cutRod(int p[], int n, int r[]);

int cutRod(int p[], int n)
{
	/* 存储钢条长度为 i 的最大分割价值 */
	int* r = new int[n + 1];
	/** 
	 * 将 r 数组元素初始为 -1
	 * 我们只需要判断该位置元素是否为 -1 便可以知道它是否被计算过
	 */
	for (int i = 0; i <= n; i++)
	{
		r[i] = -1;
	}
	return cutRod(p, n, r);
}

int cutRod(int p[], int n, int r[])
{
	/* 判断长度为 n 的钢条最大分割价值是否被计算过，计算过直接返回 */
	if (r[n] != -1)	return r[n];

	int q = INT_MIN;
	
	/* 长度为 0 的钢条最大分割价值置为0 */
	if (n == 0) q = 0;
	else
	{
		for (int i = 1; i <= n; i++)
		{
			q = max(q, p[i] + cutRod(p, n - i, r));
		}
	}
	
	/* 将长度为 n 的钢条最大分割价值记录在 r 数组中 */
	r[n] = q;
	return q;
}

int main()
{
	/* p[0] = -1, 钢条长度从 1 开始 */
	int p[] = { -1, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };
	cout << cutRod(p, 4) << endl;
}

2、自底向上法
我们之前分析时给出了两个状态方程，我们使用任意一个即可解题：

① $r_n = max(p_i + r_{n-i})$
② $r_n = max(p_n,r_1+r_{n-1},r_2+r_{n-2},…,r_{n-1}+r_1)$

使用方程 ①：

int cutRod(int p[], int len)
{
	if (len == 0)	return 0;

	int* r = new int[len + 1];

	r[0] = 0;
	for (int n = 1; n <= len; ++n)
	{
		int q = INT_MIN;
		for (int i = 1; i <= n; ++i)
		{
			q = max(q, p[i] + r[n - i]);
		}
		r[n] = q;
	}

	return r[len];
}

使用方程 ②：

int cutRod(int p[], int n)
{
	if (n == 0)	return 0;

	vector<int> r(n + 1);

	for (int j = 1; j <= n; ++j)
	{
		int q = p[j];
		/**
		 * 通过状态转移方程我们可以看出r1+rn-1 和 rn-1+r1其实是一样的。
		 * 所以没有必要循环到i,截至到i/2即可。
		 */
		for (int i = 1; i <= j/2; ++i)
		{
			q = max(q, r[i] + r[j - i]);
		}
		r[j] = q;
	}

	return r[n];
}

上述两种方法，都使用了两重循环，区别就是内层循环，外层循环的作用都是记录 $r[1],r[2]···$ ，内层循环的作用都是求出 $r[1],r[2]···$ 的最优解，也就是说 $r[i]$ 中保存的是钢条长度为 $i$ 时划分的最优解，这里面涉及到了最优子结构问题，也就是一个问题取最优解的时候，它的子问题也一定要取得最优解。

总结：结合动态规划的算法设计步骤来说，钢条切割问题也是遵守其标准的。

第一步先确定最优化解的结构特征：最优切割方案是由第一次切割后得到的两段钢条的最优切割方案组成的，或者是第一次切割后，其右端剩余部分的最优切割方案组成的。
第二步递归定义最优解的值，由上面的分析我们可以得到 $r_n = max(p_i + r_{n-i})$ ， $r_n = max(p_n,r_1+r_{n-1},r_2+r_{n-2},…,r_{n-1}+r_1)$ 两个最优解的公式，其满足求得原问题最优解的条件。
第三步根据得到的求最优解公式，计算出结果。我们用到了两种方法：带备忘的自顶向下递归法和自底向上法（非递归）。
第四步构造出最优解。

硬币问题

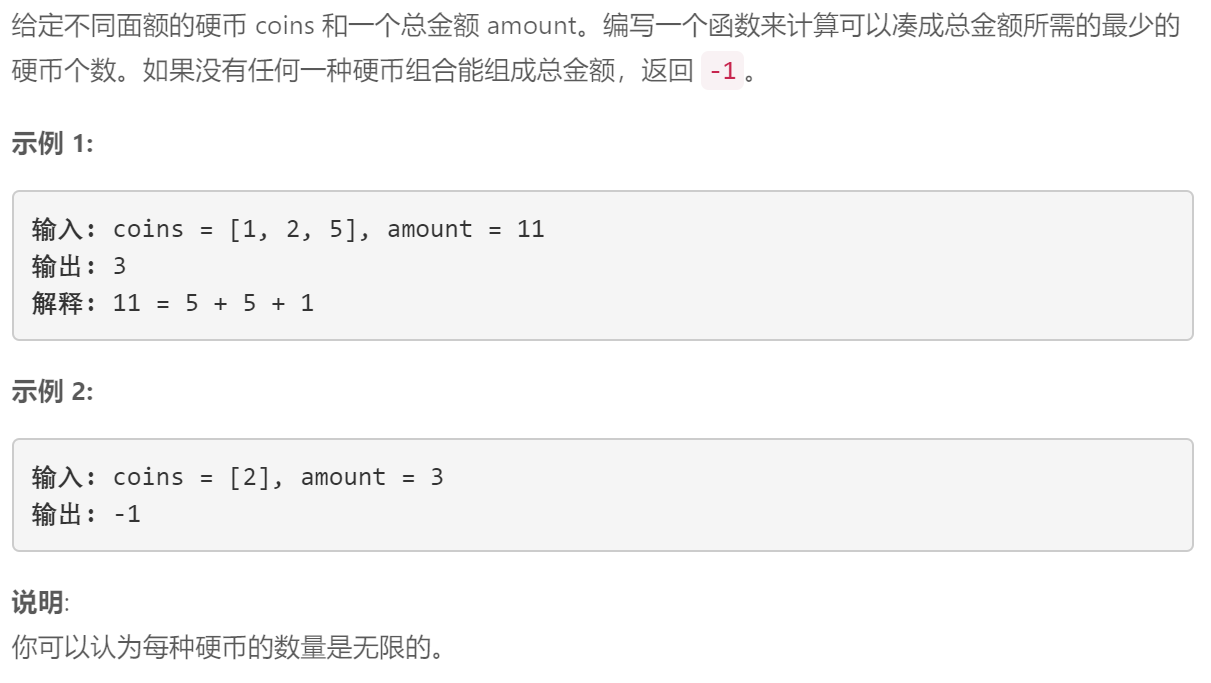
接下来我们分析一下上述问题：

我们定义凑成价值为 i 的最少硬币个数为 d[i] ，假设硬币面值为 $\{1, 3, 5\}$ ，那么，我们用 $d(i) = j$ 来表示凑够 $i$ 元最少需要 $j$ 个硬币。

当 $d(0)=0$ ，表示凑够0元最小需要0个硬币。
当 $i=1$ 时，只有面值为1元的硬币可用，因此我们拿起一个面值为1的硬币，接下来只需要凑够0元即可，而这个是已经知道答案的，即 $d(0)=0$ 。所以， $d(1)=d(1-1)+1=d(0)+1=0+1=1$ ，这里为什么要加1，是因为我们已经选择了1枚硬币。
当 $i=2$ 时，仍然只有面值为1的硬币可用，于是我拿起一个面值为1的硬币，接下来我只需要再凑够 $2-1=1$ 元即可(记得要用最小的硬币数量)，而这个答案也已经知道了。所以 $d(2)=d(2-1)+1=d(1)+1=1+1=2$ 。
当 $i=3$ 时，我们可选的硬币就有两种了：1元、3元（5元的仍然不可选，因为需要凑的数目是3元，5元面值大于3）。既然能用的硬币有两种，就有两种方案。第一种方案是拿起一个1元的硬币，那么目标就变为：凑够 $3-1=2$ 元需要的最少硬币数量。即 $d(3)=d(3-1)+1=d(2)+1=2+1=3$ 。这个方案就是拿3个1元的硬币；第二种方案是拿起一个3元的硬币，那么目标就变为：凑够 $3-3=0$ 元需要的最少硬币数量。即 $d(3)=d(3-3)+1=d(0)+1=0+1=1$ 。那么根据题意我们选择需要硬币最少的方案，即选择一个3元硬币。
当 $i = 4$ 时，两种选择：1元、3元。选择1元的： $d(4) = d(4 - 1) + 1 =d(3)+1= 2$ ；选择3元的： $d(4) = d(4 - 3) + 1 =d(1)+1= 2$ ；最少为2个硬币。
当 $i = 5$ 时，三种选择：1元、3元、5元。选择1元的： $d(5) = d(5 - 1) + 1 =d(4)+1= 3$ ；选择3元的： $d(5) = d(5 - 3) + 1 =d(2)+1= 3$ ；选择5元的： $d(5) = d(5 - 5) + 1 =d(0)+1= 1$ ，最少为1个硬币。

上文中 $d(i)$ 表示凑够 $i$ 元需要的最少硬币数量，我们将它定义为该问题的”状态”，这个状态是怎么找出来的呢？根据子问题定义状态。找到子问题，状态也就浮出水面了。

最终我们要求解的问题，可以用这个状态来表示，那么状态转移方程是什么呢？既然我们用d(i)表示状态，那么状态转移方程自然包含 $d(i)$ ，上文中包含状态d(3)的方程是： $d(3)=min\{d(3-1)+1,d(3-3)+1\}$ 。将其抽象一下就可得到该问题的状态转移方程：
$d(i)=min\{ d(i-v_j)+1 \}$ ，其中 $i-v_j >=0$ ， $v_j$ 表示第 $j$ 个硬币的面值。

有了状态和状态转移方程，这个问题基本上也就解决了，程序是很好编写的。

int coinChange(vector<int>& coins, int amount) {
	int length = coins.size();
	
	int *dp = new int[amount + 1];
	
	/* 组成0元所需的最少硬币个数是0 */
	dp[0] = 0;
	
	for(int i = 1;; i <= amount; ++i)
    {
    	/* dp[i]初始化为最大值，因为内层循环要进行min比较 */
    	dp[i] = INT_MAX - 1;
    	/* 遍历硬币面额数组*/
    	for(int j = 0; j < length; ++j)
		{
			/* 当前价值i大于该硬币的面值 */
			if(i >= coins[j])
            {
            	dp[i] = min(dp[i], dp[i - coins[j]] + 1);
            }
		}
	}
	/*  dp[i]仍为初值，表示硬币面值无法组成指定价值 */
	 if(dp[amount] == INT_MAX - 1)
            return -1;
            
	 return dp[amount];
}

最大子段和问题

问题描述：

给定n个整数（可能为负数）组成的序列 $A[1],A[2],A[3],…,A[n]$ ，求该序列如 $A[i]+A[i+1]+…+A[j]$ 的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： $max\{0,A[i]+A[i+1]+…+A[j]\},1<=i<=j<=n$ 。

例如，当 $\{A[1],A[2],A[3],A[4],A[5],A[6]\}=(-2,11,-4,13,-5,-2)$ 时，最大子段和为20。

算法分析：

最大子段和问题的动态规划解法是一种相对来说最优的解法，这种解法只需要遍历一次序列，因此时间复杂度仅为 $O(n)$ 。

使用 $dp[i]$ 表示以 $A_i$ 结尾的若干个连续子段的和的最大值，则有状态转移方程： $dp[i] = max\{dp[i-1] + A[i], A[i]\}$

算法简单描述一下就是不断的记录每一小段的当前序列和，若当前小段的序列和已经小于0时，其实我们可以认为，不管是下一个数是正数还是负数，因为当前序列和是一个负数，那么对于需要求取最大值时，它只会让后面的序列和变小。

所以，当之前记录的子序列和已经小于零的时候，我们选择果断的将其抛弃，重新开始，即从当前元素开始重新记录。需要注意的是，在每一轮循环时，我们都应当取判断当前记录的分段和是否已经大于了之前记录的最大值段和，如果已经大于了，则用当前的分段和直接替换掉之前的最大子序列和。

int maxSubArray(vector<int>& nums)
{
	int length = nums.size();
	/* dp数组存储以nums[i]结尾的若干个连续子段和的最大值 */
	int* dp = new int[length];
	/* dp[0]根据首元素的正负进行初始化 */
	dp[0] = (nums[0] >= 0 ? nums[0] : 0);
	/* 存储当前的最大子段和 */
	int maxSum = dp[0];

	for (int i = 1; i < length; i++)
	{
		/* 若之前的最大子段和为正，则把当前元素加入 */
		if (dp[i - 1] > 0)
			dp[i] = dp[i - 1] + nums[i];
		else /* 之前的最大子段和为负，抛弃之前的，从当前元素重新开始 */
			dp[i] = nums[i];
		
		/* 当前的子段和大于记录的之前的最大子段和，则进行更新 */
		if (dp[i] > maxSum)
			maxSum = dp[i];
	}
	return maxSum;
}

我们上述开辟了 $dp$ 数组来存储当前的最大子段和，我们可以对比之前讲解的斐波那契数列的空间优化，由于 $dp[i]$ 仅仅依赖上一个状态即 $dp[i-1]$ ，因此我们直接通过变量记录之前的最大子段和即可，针对空间的优化版本如下：

 int maxSubArray(vector<int>& nums) 
 {
      int length = nums.size();
      
      int maxSum = INT_MIN;
      
      /* 记录之前的最大子段和 */
      int curSum = 0;
      for(int i = 0; i < length; ++i)
      {
      	  /* 之前的最大子段和为正，累加当前元素 */
          if(curSum >= 0)	curSum += nums[i];
          /* 之前的最大子段和为负，从当前元素重新开始 */
          if(curSum < 0)	curSum = nums[i];
          
          if(curSum > maxSum)
              maxSum = curSum;
         
      }
      return maxSum;
  }

最长递增子序列（LIS）

抽象描述：

最长上升子序列（Longest Increasing Subsequence），简称LIS，也有些情况是求最长非降子序列，二者区别就是序列中是否可以有相等的数。

假设我们有一个序列 $b_i$ ，当 $b_1 < b_2 < … < b_n$ 的时候，我们称这个序列是上升的。对于给定的一个序列 $(a_1, a_2, …, a_N)$ ，我们也可以从中得到一些上升的子序列 $(a_{i1}, a{i_2}, …, a_{iK})$ ，这里 $1 <= i1 < i2 < … < iK <= N$ ，但必须按照从前到后的顺序。

比如，对于序列(1, 7, 3, 5, 9, 4, 8)，我们就会得到一些上升的子序列，如(1, 7, 9), (3, 4, 8), (1, 3, 5, 8)等等，而这些子序列中最长的，如子序列(1, 3, 5, 8) ，它的长度为4，因此该序列的最长上升子序列长度为4。

子序列、公共子序列以及最长公共子序列都不唯一，但很显然，对于固定的数组，虽然LIS序列不一定唯一，但LIS的长度是唯一的。例如给定序列 ( 1, 7, 3, 5, 9, 4, 8)，易得最长上升子序列长度为4，这是确定的，但序列可以为 ( 1, 3, 5, 8 ), 也可以为 ( 1, 3, 5, 9 )。

问题描述：

算法分析：

我们要求出 $n$ 个数的最长上升子序列，可以求前 $n-1$ 个数的最长上升子序列，再跟第 $n$ 个数进行判断。求前 $n-1$ 个数的最长上升子序列，可以通过求前 $n-2$ 个数的最长上升子序列···，直到求前1个数的最长上升子序列，此时LIS当然为1。

举个例子：求 $\{2,7,1,5,6,4,3,8,9\}$ 的最长上升子序列。我们定义 $d(i) (i∈[1,n])$ 来表示前 $i$ 个数以 $A[i]$ 结尾的最长上升子序列长度。

前1个数： $d(1)=1$ ，子序列为2；
前2个数：7之前有2小于7， $d(2)=d(1)+1=2$ ，子序列为2 7
前3个数：在1前面没有比1更小的，1自身组成长度为1的子序列 $d(3)=1$ 子序列为1
前4个数：5之前有2小于5， $d(4)=d(1)+1=2$ ，子序列为2 5
前5个数：6前面有2,5小于6， $d(5)=d(4)+1=3$ ，子序列为2 5 6
前6个数：4前面有2小于4， $d(6)=d(1)+1=2$ ，子序列为2 4
前7个数：3前面有2小于3。 $d(7)=d(1)+1=2$ ，子序列为2 3
前8个数：8前面有2,5,6小于8， $d(8)=d(5)+1=4$ ，子序列为2 5 6 8
前9个数：9前面有2.5.6 8小于9， $d(9)=d(8)+1=5$ ，子序列为2 5 6 8 9

$d(i)=max\{d(1),d(2),···,d(i)\}$ ，我们可以得出该序列的LIS为 $d(9)=5$ 。

总结一下， $d(i)$ 就是找以 $A[i]$ 结尾的，在 $A[i]$ 之前的最长上升子序列 +1，当 $A[i]$ 之前没有比 $A[i]$ 更小的数时， $d(i)=1$ 。所有的 $d(i)$ 里面最大的那个就是最长上升子序列。

状态设计： $dp[i]$ 代表以 $A[i]$ 结尾的 LIS 的长度
状态转移： $dp[i] = max \{ dp[j] + 1 ，dp[i] \} (1 <= j < i，A[j] < A[i])$
边界处理： $dp[i] = 1 (1 <= i <= n)$
时间复杂度： $O (n^2)$

int lengthOfLIS(vector<int>& nums) 
{
    int length = nums.size();
    /* dp[i]存储以A[i]结尾的LIS的长度 */
    int *dp = new int[length + 1];
    
    int maxLength = 0;
    for(int i = 0; i < length; ++i)
    {
    	/* 将A[i]结尾的LIS长度都初始化为 1 */
        dp[i] = 1;
        /* dp[i]依赖于前一个满足nums[i] > nums[0···i-1]状态的最优解 */
        for(int j = 0; j < i; ++j)
        {
        	/* 若是求最长非降子序列，此处可以等于 */
            if(nums[j] < nums[i])
            {
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
        
        /* 判断是否需要更新maxLength */
        if(dp[i] > maxLength)
            maxLength = dp[i];
    }
    
    return maxLength;
}

最长公共子序列（LCS）

概念梳理：

子序列(subsequence)：一个特定序列的子序列就是将给定序列中零个或多个元素去掉后得到的结果(不改变元素间相对次序)。例如序列
$<A,B,C,B,D,A,B>$ 的子序列有： $<A,B>$ 、 $<B,C,A>$ 、
$<A,B,C,D,A>$ 等。
公共子序列(common subsequence)：给定序列 $X$ 和 $Y$ ，序列 $Z$ 是 $X$ 的子序列，也是 $Y$ 的子序列，则 $Z$ 是 $X$ 和 $Y$ 的公共子序列。例如
$X=<A,B,C,B,D,A,B>$ ， $Y=<B,D,C,A,B,A>$ ，那么序列 $Z=<B,C,A>$ 为 $X$ 和 $Y$ 的公共子序列，其长度为3。但 $Z$ 不是 $X$ 和 $Y$ 的最长公共子序列，而序列 $<B,C,B,A>$ 和 $<B,D,A,B>$ 均为 $X$ 和 $Y$ 的最长公共子序列，长度为4。因为 $X$ 和 $Y$ 不存在长度大于等于5的公共子序列。
最长公共子序列（Longest Common Subsequence）：一个序列 S ，如果分别是两个或多个已知序列的子序列，且是所有符合此条件序列中最长的，则 S 称为已知序列的最长公共子序列。

问题描述：

给定两个序列 $X=<x_1,x_2,···,x_m>$ 和 $Y=<y_1,y_2,···,y_m>$ ，求 $X$ 和 $Y$ 长度最长的公共子序列。

算法分析：

LCS问题具有最优子结构
令 $X=<x_1,x_2,...,x_m>$ 和 $Y=<y_1,y_2,...,y_n>$ 为两个序列， $Z=<z_1,z_2,z_3,...,z_k>$ 为 $X$ 和 $Y$ 的任意LCS。则

如果 $x_m=y_n$ ，则 $z_k=x_m=y_n$ 且 $Z_{k−1}$ 是 $X_{m−1}$ 和 $Y_{n−1}$ 的一个LCS。
如果 $x_m≠y_n$ ，那么 $z_k≠x_m$ ，意味着 $Z$ 是 $X_{m−1}$ 和 $Y$ 的一个LCS。、
如果 $x_m≠y_n$ ，那么 $z_k≠y_n$ ，意味着 $Z$ 是 $X$ 和 $Y_{n−1}$ 的一个LCS。

从上述的结论可以看出，两个序列的LCS问题包含两个序列的前缀的LCS，因此，LCS问题具有最优子结构性质。在设计递归算法时，不难看出递归算法具有子问题重叠的性质。

设 $C[i,j]$ 表示 $X_i$ 和 $Y_j$ 的最长公共子序列LCS的长度。如果 $i=0$ 或 $j=0$ ,即一个序列长度为0时，那么LCS的长度为0。根据LCS问题的最优子结构性质，可得如下公式：

$C[i][j]=\left\{ \begin{array}{lcl} 0 & & {若i=0或j=0}\\ C[i-1][j-1] && {若i,j＞0且x_i=y_i}\\ max(C[i][j-1],C[i-1][j])&& {若i,j＞0且x_i≠y_i} \end{array}\right.$

① 朴素递归算法描述：

int LCS(string str1, string str2, int m, int n)
{
	int maxLength = 0;
	/* 任何一个序列长度为0，直接返回0 */
	if (m == 0 || n == 0}	return 0;
	
	if (str1[m] == str2[n]){
		maxLength = LCS(str1, str2, m - 1, n - 1) + 1;
	else
		maxLength = max(LCS(str1, str2, m, n - 1), LCS(str1, str2, m - 1, n));
		
	return maxLength;
}

上述代码简洁，但是这种朴素的递归算法会导致大量的重叠子问题被重复的计算，导致算法的效率低下，因此我们可以使用带备忘的自顶向下法解决。、

② 带备忘的自顶向下法描述

int LCS(string str1, string str2, int m, int n, vector<vector<int>>& dp);

int LCS(string str1, string str2, int m, int n)
{
	/* 定义dp数组存储Xm和Yn的LCS的长度 */
	vector<vector<int>> dp(m + 1, vector<int>(n + 1));
	for (int i = 0; i < m; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			dp[i][j] = 0; // 数组元素的初始化
		}
	}

	return LCS(str1, str2, m, n, dp);
}

int LCS(string str1, string str2, int m, int n, vector<vector<int>> &dp)
{
	/* 任何一个序列长度为0，直接返回0 */
	if (m == 0 || n == 0)
		return 0;
	/* 若dp[m][n]不为0，说明已经计算过，直接返回其值就可以，不必重新计算 */
	if (dp[m][n] > 0)
		return dp[m][n];

	int maxLength = 0;

	if (str1[m] == str2[n])
	{
		dp[m][n] = LCS(str1, str2, m - 1, n - 1, dp) + 1;
	}
	else
	{
		dp[m][n] = max(LCS(str1, str2, m, n - 1, dp), LCS(str1, str2, m - 1, n, dp));
	}

	return dp[m][n];
}

带备忘的自顶向下法解决了朴素递归算法对于重叠子问题的重复计算，但是备忘录法的动态规划仍然是基于递归实现的，算出 $dp[m][n]$ 就要递归的算出之前的值，我们可以不使用递归，首先迭代计算之前的值，最后计算出 $dp[m][n]$ ，采用自底向上的动态规划算法。

③ 自底向上的动态规划算法描述（非递归）

int LCS(string str1, string str2, int m, int n)
{
	vector<vector<int>> dp(m + 1, vector<int>(n + 1));
	
	/* 任何一个序列长度为0，该状态的dp就置为0 */
	for (int i = 0; i <= m; ++i) dp[i][0] = 0;
	for (int j = 0; j <= n; ++j) dp[0][j] = 0;


	for (int i = 1; i <= m; ++i)
	{
		for (int j = 1; j <= n; ++j)
		{
			if (str1[i - 1] == str2[j - 1])
			{
				dp[i][j] = dp[i - 1][j - 1] + 1;
			}
			else
			{
				dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
			}
		}
	}

	return dp[m][n];
}

我们使用了以上三种方法来求解LCS的最大长度，那么如何求解出LCS的具体序列呢？

为了解决这个问题，我们需要维护一个表 $b[0···m][0···n]$ 来帮助构造最优解， $b[i][j]$ 指向的表项对应计算 $dp[i][j]$ 时所选择子问题的最优解。

/* 辅助数组使我们在外部创建的，因为LCS打印函数要使用辅助表b */
int LCS(string str1, string str2, int m, int n, vector<vector<int>>& b)
{
	vector<vector<int>> dp(m + 1, vector<int>(n + 1));
	
	for (int i = 0; i <= m; ++i) dp[i][0] = 0;
	for (int j = 0; j <= n; ++j) dp[0][j] = 0;
		
	for (int i = 1; i <= m; ++i)
	{
		for (int j = 1; j <= n; ++j)
		{
			if (str1[i - 1] == str2[j - 1])
			{
				dp[i][j] = dp[i - 1][j - 1] + 1;
				b[i][j] = 1; /* 辅助数组为1表示LCS路径向对角线方向查找 */
			}
			else
			{
				if (dp[i][j - 1] >= dp[i - 1][j])
				{
					dp[i][j] = dp[i][j - 1];
					b[i][j] = 2;/* 辅助数组为2表示LCS路径向左查找 */
				}
				else
				{
					dp[i][j] = dp[i - 1][j];
					b[i][j] = 3;/* 辅助数组为3表示LCS路径向上查找 */
				}
			}
		}
	}
	return dp[m][n];
}

/* TraceBack负责在LCS函数执行完毕后根据辅助表b打印LCS */
void TraceBack(string str1, int m, int n, vector<vector<int>>& b)
{
	if (m == 0 || n == 0)
		return;
	
	/*  */
	if (b[m][n] == 1)
	{	
		TraceBack(str1, m - 1, n - 1, b);
		cout << str1[m - 1];
	}
	else if (b[m][n] == 2)
	{
		TraceBack(str1, m, n - 1, b);
	}
	else
	{
		TraceBack(str1, m - 1, n, b);
	}
}

0-1背包问题

问题描述：

给定一个背包，已知背包容量为 $c$ ，再给出 $n$ 件物品，物品的重量存储在 $w[]$ 数组中，物品的价值存储在 $v[]$ 数组中，物品 $i$ 的重量为 $w[i]$ ，其价值为 $v[i]$ 。问应如何选择装入背包中的物品，使得背入背包的物品的总价值最大？

算法描述：

这是一个典型的动态规划求解。0-1背包问题，对于每件物品而言，只有两种选择，要么选中它装入背包；要么不选它。

有两种方法，基本思想相同，只是状态转移方程不同，我们现在首先来分析一下第一种方法。

设所给0-1背包问题的子问题的最优值为 $m[i][j]$ , 即 $m[i][j]$ 的含义是是在背包容量为 $j$ ，可选物品为 $1, 2, 3, ..., i$ 时的0-1背包问题的最优值。由0-1背包问题的最优子结构性质，可建立计算 $m[i][j]$ 的递归式如下：
$m[0][j]=\left\{ \begin{array}{lcl} v[0]&& { j≥w[i]}\\ 0 && {0≤ j＜w[i]}\\ \end{array}\right.$

$m[i][j]=\left\{ \begin{array}{lcl} max\{m[i - 1][j],m[i-1][j-w[i]] + v[i]\}&& { j≥w[i]}\\ m[i-1][j] && {0≤ j＜w[i]}\\ \end{array}\right.$

如果不放入第 $i$ 件物品，则问题转换为“前 $i - 1$ 件物品放入容量为 $j$ 的背包中”；
如果放入第 $i$ 件物品，则问题转化为“前 $i - 1$ 件物品放入容量为 $j - w[i]$ 的背包中”，此时的最大值为 $max\{m[i - 1][j], m[i - 1][j - w[i]] + v[i]\}$

void Knapsack(int v[], int w[], int n, int c, vector<vector<int>>& dp)
{
	for (int j = 0; j <= c; ++j)
	{
		/* 处理第一个物品 */
		if (j < w[0])
		{
			dp[0][j] = 0;
		}
		else
		{
			dp[0][j] = v[0];
		}
	}
	/* 处理之后的 n - 1个物品 */	
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= c; j++)
		{
			if (j < w[i])
			{
				dp[i][j] = dp[i - 1][j];
			}
			else
			{
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
			}
		}
	}

	cout << dp[n][c] << endl;
}

void TraceBack(vector<vector<int>>& dp, int w[], int v[], int c, int n, vector<int> &x)
{
	int bestv = 0;
	/* 最后的最优值肯定在末行出现 */
	for (int i = n; i > 0; --i)
	{
		if (dp[i][c] == dp[i - 1][c])
		{
			x[i] = 0;
		}
		else
		{
			bestv += v[i];
			x[i] = 1;
			c -= w[i];
		}
	}
	/* 判断第一个物品是否被放入了背包 */
	if (dp[0][c] > 0)
	{
		bestv += v[0];
		x[0] = 1;
	}

	for (int val : x)
		cout << val << " ";
	cout << endl;

	cout << bestv << endl;
}

int main()
{
	int w[] = { 8,6,4,2,5 };
	int v[] = { 6,4,7,8,6 };
	int c = 20;

	int length = sizeof(w) / sizeof(w[0]);

	vector<vector<int>> dp(length, vector<int>(c + 1));
	vector<int> x(length);
	Knapsack(v, w, length - 1, c, dp);
	TraceBack(dp, w, v, c, length - 1, x);
	cout << endl;
}

接下来我们看一下第二种状态转移方程：
$m[n][j]=\left\{ \begin{array}{lcl} v[n]&& { j≥w[i]}\\ 0 && {0≤ j＜w[i]}\\ \end{array}\right.$

$m[i][j]=\left\{ \begin{array}{lcl} max\{m[i + 1][j],m[i+1][j-w[i]] + v[i]\}&& { j≥w[i]}\\ m[i+1][j] && {0≤ j＜w[i]}\\ \end{array}\right.$

如果不放入第 $i$ 件物品，则问题转换为“之后的 $n-i$ 件物品放入容量为 $j$ 的背包中”；
如果放入第 $i$ 件物品，则问题转化为“之后的 $n-i$ 件物品放入容量为 $j - w[i]$ 的背包中”，此时的最大值为 $max\{m[i + 1][j], m[i +1][j - w[i]] + v[i]\}$ 。

void Knapsack(int v[], int w[], int n, int c, vector<vector<int>>& dp)
{
	/* 先处理最后一个物品 */		
	for (int j = 0; j <= c; ++j)
	{
		if (j < w[n])
		{
			dp[n][j] = 0;
		}
		else
		{
			dp[n][j] = v[n];
		}
	}
	/* 处理前n-1个物品 */
	for (int i = n - 1; i >= 0; --i)
	{
		for (int j = 1; j <= c; ++j)
		{
			if (j < w[i])
			{
				dp[i][j] = dp[i + 1][j];
			}
			else
			{
				dp[i][j] = max(dp[i + 1][j], dp[i + 1][j - w[i]] + v[i]);
			}
		}
	}
}

void TraceBack(vector<vector<int>>& dp, int w[], int v[], int c, int n, vector<int>& x)
{
	int bestv = 0;
	/* 最后的最优值肯定在首行出现 */
	for (int i = 0; i < n; ++i)
	{
		if (dp[i][c] == dp[i + 1][c])
		{
			x[i] = 0;
		}
		else
		{
			x[i] = 1;
			bestv += v[i];
			c -= w[i];
		}
	}
	/* 判断最后一个物品是否被放入了背包 */
	if (dp[n][c] > 0)
	{
		x[n] = 1;
		bestv += v[n];
	}

	cout << bestv << endl;
}

int main()
{
	int w[] = { 8,6,4,2,5 };
	int v[] = { 6,4,7,8,6 };
	int c = 20;

	int length = sizeof(w) / sizeof(w[0]);

	vector<vector<int>> dp(length, vector<int>(c + 1));
	vector<int> x(length);
	Knapsack(v, w, length - 1, c, dp);
	TraceBack(dp, w, v, c, length - 1, x);
	for (int val : x)
	{
		cout << val << " ";
	}
	cout << endl;
}

《金矿模型》
《动态规划的经典模型》