【机器学习算法推导】高斯混合模型GMM与EM算法

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/Hemk340200600/article/details/86498601

1.高斯混合模型（GMM）

  极大似然估计是一种应用很广泛的参数估计方法。在已有某个地区身高数据以及知道身高服从高斯分布的情况下，利用极大似然估计的方法可以估计出高斯分布 $\mu,\sigma$两个参数。
  如果是多组数据，多个模型呢？获取现在我们有全国多个省份的身高数据，但并不知道它们具体属于哪个省份，只知道每个省之间服从不同的高斯分布，此时的模型称为高斯混合模型（GMM），其公式为
$P(x;\theta)=\sum_{i=1}^k\alpha_k\phi(x;\theta_k)..........(1)$
  此时用极大似然估计的方法并不能很好地求出模型里面的参数，因为模型中存在一个隐变量——样本的label。令其为Z，则可以写出似然函数的形式：
$L(\theta)=\sum_{i=1}^m\log p(x_i;\theta)=\sum_{i=1}^m\log \sum_Zp(x_i,Z;\theta)..........(2)$
  如果根据极大似然估计的算法对式子(2)进行求导，意味着我们要对 $\log (x1+x2+...)$的形式进行求导，这计算量简直爆炸。

2.Jensen不等式

  这里我们需要用到EM算法来进行求解，在介绍EM算法前，我们先来了解一个不等式——Jensen不等式，它的定义如下：
  如果X是一个随机变量，f(X)是一个凸函数（二阶导数大或等于0），那么有：
$E(f(x)) \ge f[E(x)]$
  如果f（X）是凹函数，不等号反向
$E(f(x)) \le f[E(x)]$
  当且仅当X是常数的时候等号成立。

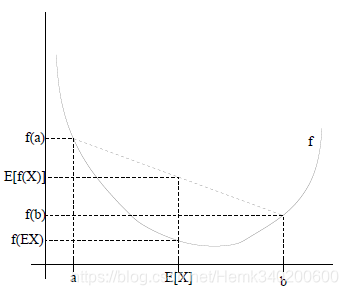
  结合图像我们可以对Jensen不等式有一个直观的理解，对于x=a和x=b两个点，E(f(x))可以看成是 $\frac{1}{2}(f(a)+f(b))$，f[E(x)]可以看成是 $f(\frac{1}{2}(f(a)+f(b)))$，即ab中点对应的函数值。由于图像是凹图像，所以不难得出 $E(f(x)) \ge f[E(x)]$。

3.EM算法及推导过程

  利用Jensen不等式，由于log函数是凹函数，式子(2)可以改写成：
$\begin{aligned} \sum_{i=1}^m\log \sum_Zp(x_i,Z;\theta) &=\sum_{i=1}^m\log \sum_{z_i}Q(z)\frac{P(x_i,z;\theta)}{Q(z)}\\ &\ge \sum_{i=1}^m\sum_{z_i}Q(z)\log \frac{P(x_i,z;\theta)}{Q(z)}..........(3) \end{aligned}$
  由于 $Q(z)$是概率分布，所以满足
$\sum_zQ(z)=1..........(4)$
  根据Jenson不等式，等式成立时，有
$\frac{p(x_i,z;\theta)}{Q(z)}=C..........(5)$
  根据4和5，有
$\sum_{z_i}Q(z)=\sum_{z_i}\frac{p(x_i,z;\theta)}{C}=1..........(6) \\ Q(z)=\frac{p(x_i,z;\theta)}{C}=\frac{p(x_i,z;\theta)}{\sum_{z}p(x_i,z;\theta)}=\frac{p(x_i,z;\theta)}{p(x_i)}=p(z|x_i;\theta)..........(7)$
  因此，EM算法的流程如下：

1. 初始化参数θ
2. E-Step：根据 $Q(z)=p(z|x_i;\theta)$计算每个样本属于zi的概率。
3. M-Step：根据计算得到的Q，得到含有θ的似然函数 $L(\theta,\bar \theta)=\sum\limits_{i=1}^m\sum\limits_{z^{(i)}}Q(z^{(i)})\log P(x^{(i)},z^{(i)};\theta)$的下界并最大化它，得到新的参数θ
4. 重复2和3直至收敛

  为什么EM算法能保证收敛呢？要证明EM算法收敛，则我们需要证明我们的对数似然函数的值在迭代的过程中一直在增大。假设当前迭代到第i轮，参数为 $\theta_i$，希望新估计值 $\theta$可以使 $L(\theta)$增大，即 $L(\theta)\gt L(\theta_i)$，则：　
$\begin{aligned} L(\theta)-L(\theta_{i}) &=\log (\sum_Zp(x|z,\theta)p(z|\theta))-\log \left(p(x|\theta_{i})\right) \\ &=\log \sum_Zp(z|x,\theta_{i})\frac{p(x|z,\theta)p(z|\theta)}{p(z|x,\theta_{i})}-\log \left(p(x|\theta_{i})\right)\\ &\ge \sum_Zp(z|x,\theta_{i})\log\frac{p(x|z,\theta)p(z|\theta)}{p(z|x,\theta_{i})}-\log \left(p(x|\theta_{i})\right)\\ &= \sum_Zp(z|x,\theta_{i})\log\frac{p(x|z,\theta)p(z|\theta)}{p(z|x,\theta_{i})(p(x|\theta_{i})} \end{aligned}$
  令 $H(\theta,\theta_{i})=L(\theta_{i})+\sum_Zp(z|x,\theta_{i})\log\frac{p(x|z,\theta)p(z|\theta)}{p(z|x,\theta_{i})(p(x|\theta_{i})}$
  则有 $L(\theta)\ge H(\theta,\theta_{i})$，因此可以认为 $H(\theta,\theta_{i})$为 $L(\theta)$的一个下界，且有 $L(\theta_{i})=H(\theta_{i},\theta_{i})$，为了使 $L(\theta)$尽可能地变大，我们解以下式子：
$\begin{aligned} \arg \max_\theta H(\theta,\theta_{i}) &=\arg \max_\theta L(\theta_{i})+ \sum_Zp(z|x,\theta_{i})\log\frac{p(x|z,\theta)p(z|\theta)}{p(z|x,\theta_{i})(p(x|\theta_{i})} \\ &= \arg \max_\theta \sum_Zp(z|x,\theta_{i})\log (p(x|z,\theta)p(z|\theta)) \\ &= \arg \max_\theta \sum_Zp(z|x,\theta_{i})p(x|z,\theta)p(z|\theta) \\ &= \arg \max_\theta \sum_Zp(z|x,\theta_{i})p(x,z|\theta) \end{aligned}$
  而这正是E-step中我们所做的工作，由此可证EM算法确实是可以收敛的。由于采用迭代的方式进行求解，EM算法可以保证收敛到一个稳定点，但是却不能保证收敛到全局的极大值点，因此它是局部最优的算法，当然，如果我们的优化目标 $H(\theta,\theta_i)$是凸的，则EM算法可以保证收敛到全局最大值，这点和梯度下降法这样的迭代算法相同。