一、预备知识
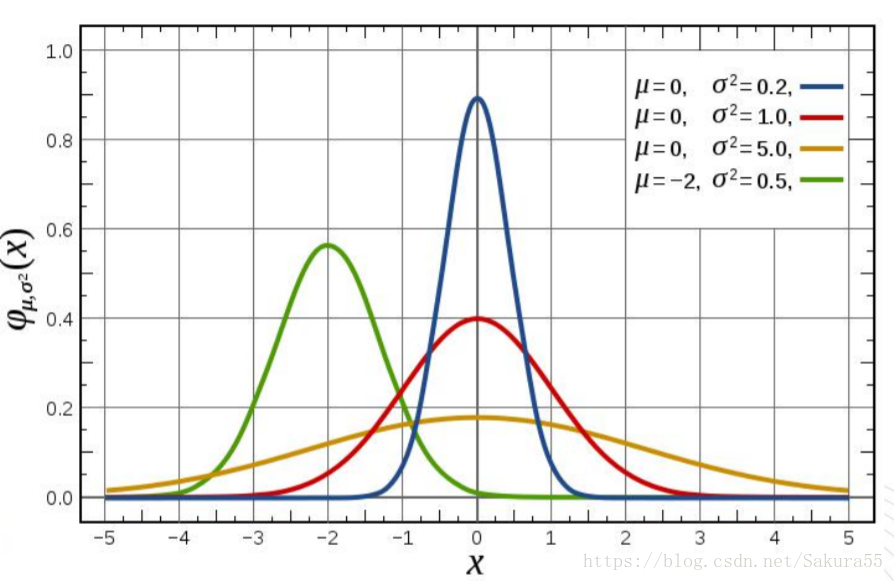
1.1、协方差矩阵
在高维计算协方差的时候,分母是n-1,而不是n。协方差矩阵的大小与维度相同。
1.2、黑塞矩阵
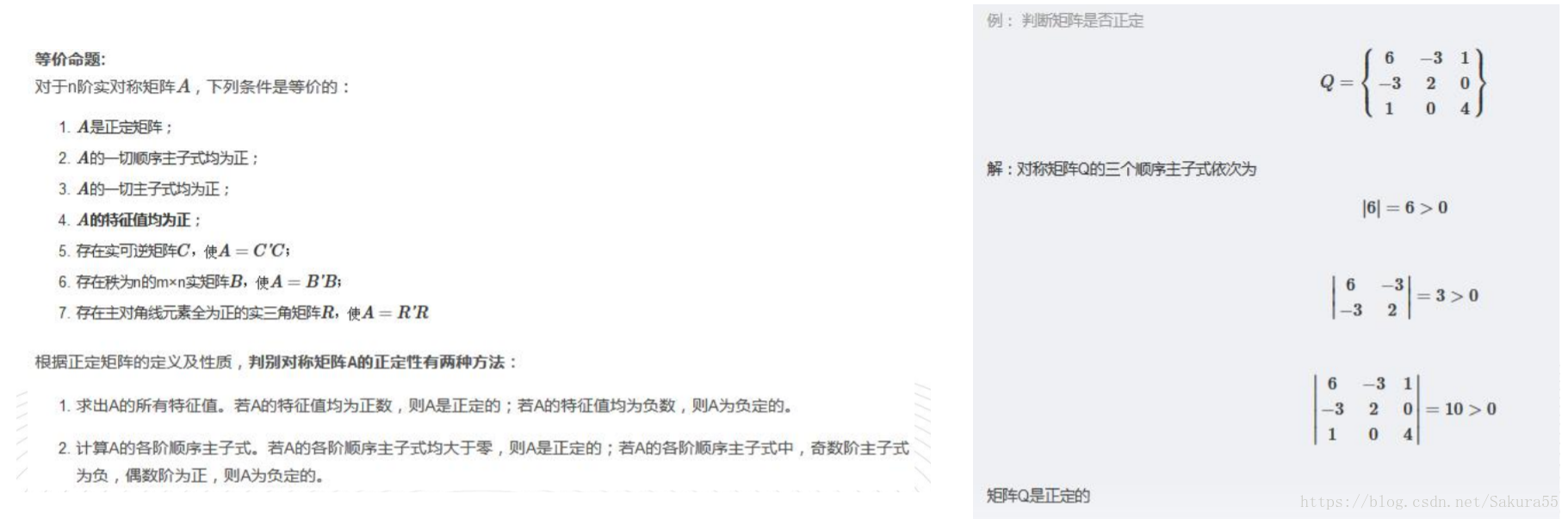
1.3、正定矩阵


二、高斯混合模型
点模式的分析中,一般会考察如下五种内容:
● 点的疏密,包括点数据的分布探索,是否一致、均匀或者不均匀。
● 点的方位,包括点的分布和方向。
● 点的数量:多少(极值和均值)。
● 点的大小:代表的含义(如点一个点代表多少人口)。
● 其他,如点的一些动态变化等。
2.1、标准差椭圆
这算法最早是由美国南加州大学(UniversityofSouthern California)社会学教授韦尔蒂.利菲弗(D. Welty Lefever)在1926年提出,所以有的书里面,也把这个算法称为Lefever‘s “Standard
DeviationalEllipse”(利菲弗方向性分布)(又到每天的历史起源科普时间……)
其实算法很简单,要画出一个椭圆:
1、确定圆心。
2、确定旋转角度。
3、确定XY轴的长度。

基本概念:
1、椭圆的长半轴表示的是数据分布的方向,短半轴表示的是数据分布的范围,长短半轴的值差距越大(扁率越大),表示数据的方向性越明显。反之,如果长短半轴越接近,表示方向性越不明显。如果长短半轴完全相等,就等于是一个圆了,圆的话就表示没有任何的方向特征。
2、短半轴表示数据分布的范围,短半轴越短,表示数据呈现的向心力越明显;反之,短轴越长,表示数据的离散程度越大。同样,如果短半轴与长半轴完全相等了,就表示数据没有任何的分布特征。
3、中心点表示了整个数据的中心位置,一般来说,只要数据的变异程度不是很大的话,这个中心点的位置大约与算数平均数的位置基本上是一致的,至于数据变异是什么情况,请看下面第4点。
4、有的同学会很疑惑,为什么你画的这个椭圆,还有很多的点都在外面,没有把所有的点都包含进去?那么就是就是“标准差椭圆”这个名词里面的“标准差”的含义所在了。
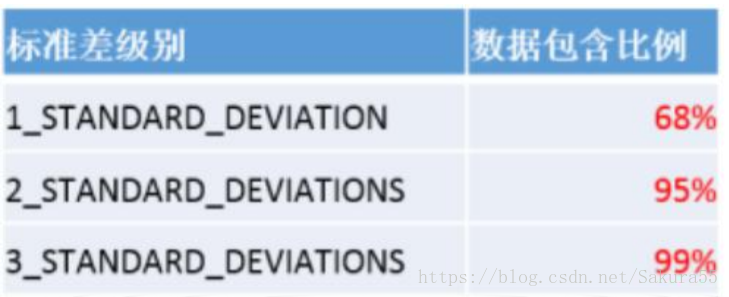
当要素具有空间正态分布时(即这些要素在中心处最为密集,而在接近外围时会逐渐变得稀疏),第一级标准差(默认值)范围可将约占总数 68%的输入要素的质心包含在内。第二级标准差范围会将约占总数 95%的要素包含在内,而第三级标准差范围则会覆盖约占总数 99%的要素的质心。
所以,当你选择不同标准差等级的时候,你发现你的中心点的位置也可能不同。当然,作为空间分析工具,方向分布一样可以进行加权计算,这个计算主要还是与中心点的位置确定以及椭圆标准差等级生成的椭圆大小有关系。
2.2、高斯混合模型(GMM)
高斯混合模型(Gaussian Mixed Model)指的是多个斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,通常用于解决同一集合下的数据包含多个不同的分布的情况(或者是同一类分布但参数不一样,或者是不同类型的分布,比如正态分布和伯努利分布)。
如图1,图中的点在我们看来明显分成两个聚类。这两个聚类中的点分别通过两个不同的正态分布随机生成而来。但是如果没有GMM,那么只能用一个的二维高斯分布来描述图1中的数据。图1中的椭圆即为二倍标准差的正态分布椭圆。这显然不太合理,毕竟肉眼一看就觉得应该把它们分成两类。
这时候就可以使用GMM了!如图2,数据在平面上的空间分布和图1一样,这时使用两个二维高斯分布来描述图2中的数据,分别记为N(μ1,Σ1)和N(μ2,Σ2). 图中的两个椭圆分别是这两个高斯分布的二倍标准差椭圆。可以看到使用两个二维高斯分布来描述图中的数据显然更合理。实际上图中的两个聚类的中的点是通过两个不同的正态分布随机生成而来。如果将两个二维高斯分布N(μ1,Σ1)和N(μ2,Σ2)合成一个二维的分布,那么就可以用合成后的分布来描述图2中的所有点。最直观的方法就是对这两个二维高斯分布做线性组合,用线性组合后的分布来描述整个集合中的数据。这就是高斯混合模型(GMM)。
从上面的分析中我们可以看到 GMM 和 K-means 的迭代求解法其实非常相似(都可以追溯到 EM 算法),因此也有和 K-means 同样的问题──并不能保证总是能取到全局最优,如果运气比较差,取到不好的初始值,就有可能得到很差的结果。对于 K-means 的情况,我们通常是重复一定次数然后取最好的结果,不过 GMM每一次迭代的计算量比 K-means 要大许多,一个更流行的做法是先用 K-means(已经重复并取最优值了)得到一个粗略的结果,然后将其作为初值(只要将 K- means 所得的 centroids 传入 gmm 函数即可),再用 GMM 进行细致迭代
2.3、多元高斯混合
2.4、应用场景
设样本集X=x1,x2,…,xN,其中N=100 ,p(xi|θ)为概率密度函数,表示抽到男生xi(的身高)的概率。由于100个样本之间独立同分布,所以我同时抽到这100个男生的概率就是他们各自概率的乘积,也就是样本集X中各个样本的联合概率,用下式表示:
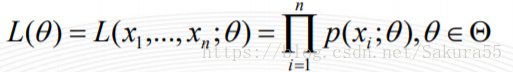
这个概率反映了,在概率密度函数的参数是θ时,得到X这组样本的概率。 我们需要找到一个参数θ,使得抽到X这组样本的概率最大,也就是说需要其对应的似然函数L(θ)最大。满足条件的θ叫做θ的最大似然估计量,记为
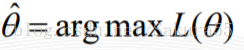
2.5、kmeans应用

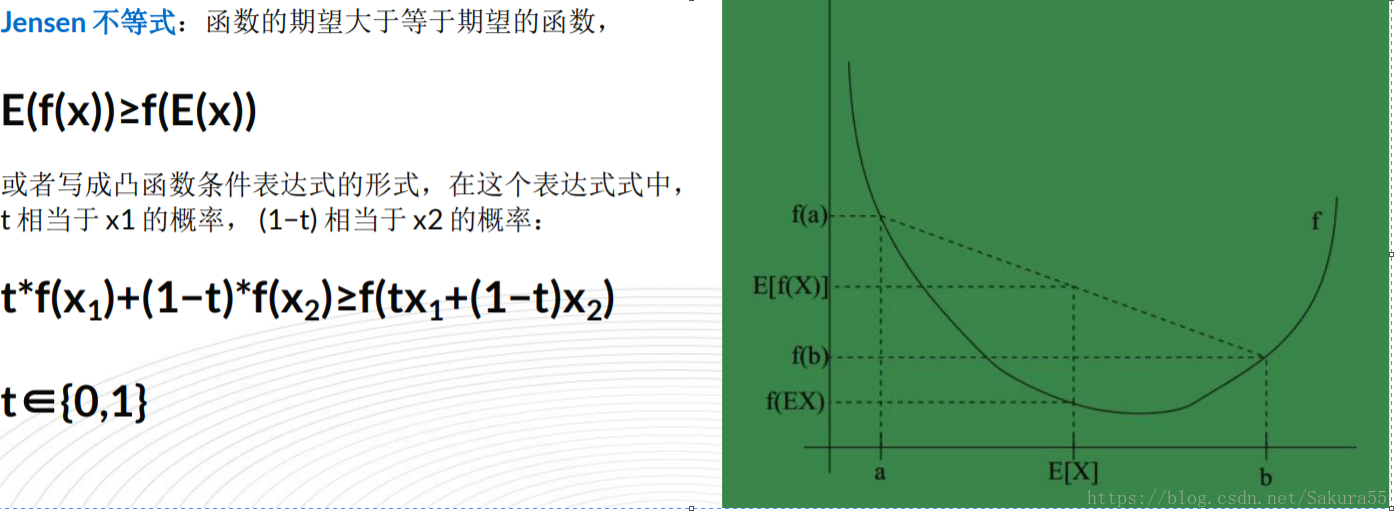
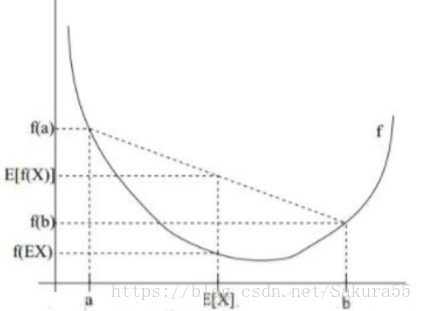
2.6、基本Jensen不等式应用

设f是定义域为实数的函数,如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是凸函数。Jensen不等式表述如下:如果f是凸函数,X是随机变量,那么E[f(X)]≥f(E[X])。当且仅当X是常量时,上式取等号。其中,E[x]表示x的数学期望。
1、Jensen不等式应用于凹函数时,不等号方向反向。当且仅当X是常量时,Jensen不等式等号成立。
2、关于凸函数,百度百科中是这样解释的——“对于实数集上的凸函数,一般的判别方法是求它的二阶导数,如果其二阶导数在区间上非负,就称为凸函数(向下凸)”。
例如,实线f是凸函数,X是随机变量,有0.5的概率是a,有0.5的概率是b。X的期望值就是a和b的中值了,图中可以看到E[f(X)]≥f(E[X])成立。
三、计算流程
(1)初始化参数:先初始化男生身高的正态分布的参数:如均值=1.7,方差=0.1
(2)计算每一个人更可能属于男生分布或者女生分布;
(3)通过分为男生的n个人来重新估计男生身高分布的参数(最大似然估计),女生分布也按照相同的方式估计出来,更新分布。
(4)这时候两个分布的概率也变了,然后重复步骤(1)至(3),直到参数不发生变化为止。
已知的有两个:
样本服从的分布模型、随机抽取的样本;
未知的有一个:
模型的参数;
根据已知条件,通过极大似然估计,求出未知参数。极大似然估计就是用来估计模型参数的统计学方法。
EM流程
有时候因为样本的产生和隐含变量有关(隐含变量是不能观察的),而求模型的参数时一般采用最大似然估计,由于含有了隐含变量,所以对似然函数参数求导是求不出来的,这时可以采用EM算法来求模型的参数的(对应模型参数个数可能有多个),EM算法一般分为2步:
E步:选取一组参数,求出在该参数下隐含变量的条件概率值;
M步:结合E步求出的隐含变量条件概率,求出似然函数下界函数(本质上是某个期望函数)的最大值。
重复上面2步直至收敛: