支持向量机详解之——系列2

间隔最大化最优值求解方法

        上节得到了线性可分支持向量机学习的最优化问题，即原始问题：

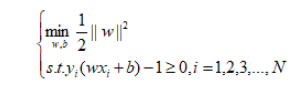
由于目标函数 $\frac{1}{2}||w||_2^2$是凸函数，同时约束条件不等式是仿射，所以这是一个凸二次规划问题。

一、拉格朗日乘数法

        上述优化函数是一个比较典型的有限制条件的求多元函数极值的问题，为了求解此最优化函数，需要应用拉格朗日对偶性，通过求解对偶问题得到原始问题的最优解。那么下面，首先将简单证明下等式条件下拉格朗日乘数法的来历和KKT条件的数学推理。

1. 拉格朗日乘数法基本思想

        拉格朗日乘子法作为一种优化算法，主要用于解决约束优化问题，它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数（或者说，拉格朗日乘子是约束条件边界直线的法向量与目标函数等高线的法向量是共线向量）。

        如何将一个含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题？拉格朗日乘数法从数学意义入手，通过引入拉格朗日乘子建立极值条件，对n个变量分别求偏导对应了n个方程，然后加上k个约束条件（对应k个拉格朗日乘子）一起构成包含了（n+k）变量的（n+k）个方程的方程组问题，这样就能根据求方程组的方法对其进行求解。

等式约束问题可以如下的表示：
即：min / max f(x,y,z)
　　s.t. g(x,y,z)=0

数学实例： 求双曲线xy=3上离原点最近的点？
转化为约束优化问题：
min f(x,y)=x2+y2
s.t. xy=3
        我们将 x2+y2=c 的曲线族画出来，如下图所示，当曲线族中的圆与xy=3曲线进行相切时，切点到原点的距离最短。就可得到上述优化问题的一个极值。

        如果两个曲线相切，那么它们的切线相同，即法向量是相互平行的，▽f // ▽g，由 ▽f // ▽g可以得到，▽f = λ*▽g。这时，我们将原有的约束优化问题转化为了一种对偶的无约束的优化问题，如下所示：

        通过求解右边的方程组我们可以获取原问题的解。通过举上述这个简单的例子就是为了体会拉格朗日乘数法的思想，即通过引入拉格朗日乘子(λ)将原来的约束优化问题转化为无约束的方程组问题。

通过实例理解了拉格朗日乘数法的思后，下面证明下拉格朗日乘子法：

2. 拉格朗日乘数法的基本形式

为求函数

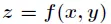
在满足

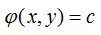
下的条件极值，将其可以转化为函数

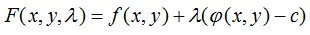
的无条件极值问题。

从图上可以直观地看到在最优解处，f 和 g 的斜率平行。
▽ [ f(x,y) + λ ( g(x,y)− c ) ] = 0, λ≠0

一旦求出 λ 的值，将其套入下式，易求在无约束极值和极值所对应的点。
F(x,y) = f(x,y) + λ(g(x,y)−c)

3. 拉格朗日乘数法与KKT条件

        上述讨论的问题均为等式约束优化问题，但是此时仍旧解决不了约束条件是不等式约束的情况，解决此问题不光需要引入拉格朗日乘子，还需要引入一个KKT条件，而拉格朗日乘数法增加了KKT条件之后便可以用拉格朗日乘数法来求解不等式约束的优化问题了。
所有的不等式约束问题可以如下的表示：

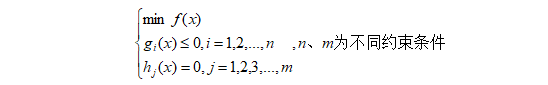
其中f(x)是目标函数，g(x)为不等式约束，h(x)为等式约束。

• 若f(x)，h(x)，g(x)三个函数都是线性函数，则该优化问题称为线性规划；
• 若任意一个是非线性函数，则称为非线性规划；
• 若目标函数f(x)为二次函数，约束全为线性函数，称为二次规划；
• 若f(x)为凸函数，g(x)为凸函数，h(x)为线性函数，则该问题称为凸优化；
• 注意这里不等式约束g(x)<=0则要求g(x)为凸函数，若g(x)>=0则要求g(x)为凹函数
• 凸优化的任一局部极值点也是全局极值点，局部最优也是全局最优；

        对于不等式约束g(x)<=0，和等式约束不一样，等式约束可以在平面上画出一条等高线，而g(x)<=0是一个区域，很多个等高线堆叠而成的一块区域，我们把这块区域称为可行域。

不等式约束分两种情况来讨论：

• 第一种是极小值点落在可行域内（不包含边界）
  

• 第二种是极小值点落在可行域外（包含边界）
  

• 极小值点落在可行域内（不包含边界）：这个时候可行域的限制不起作用，相当于没有约束，直接f(x)的梯度等于0求解，这个时候g(x极小值点)<0（因为落在可行域内）。

• 极小值点落在可行域外（包含边界）：可行域的限制起作用，极小值点应该落在可行域边界上即g(x)=0，类似于等值约束，此时有g(x)的梯度和f(x)的负梯度同向。
  

        总结以上两种情况，可以构造拉格朗日函数来转换求解问题。对于不等式约束的优化，需要满足三个条件，满足这三个条件的解 x* 就是极小值点，这三个条件就是著名的KKT条件。
特别注意：优化问题是凸优化的话，KKT条件就是极小值点（而且是全局极小）存在的充要条件。

不是凸优化的话，还需要附加多一个正定的条件才能变成充要条件，如下图所示。

        对于同时有多个等式约束和多个不等式约束，构造的拉格朗日函数就是在目标函数后面把这些约束相应的加起来，KKT条件也是如此，如下图所示。

• 简单总结一下，考虑凸优化问题。

• 对于无约束的优化问题，直接令梯度等于0求解。

• 对于含有等式约束的优化问题，拉格朗日乘子法，构造拉格朗日函数，令偏导为0求解。

• 对于含有不等式约束的优化问题，同样构造拉格朗日函数，利用KKT条件求解。

二、拉格朗日对偶性

        上节介绍了拉格朗日乘子法和KKT条件，下面总结下拉格朗日对偶性的问题。在约束优化问题中，常常用拉格朗日对偶性来将原始问题转为对偶问题，通过解对偶问题的解来得到原始问题的解。

• 为什么要利用对偶？
  首先要明确，对偶问题的解不一定直接等于原问题的解（弱对偶），但是，对偶问题有两点性质。
• 满足某些条件时，对偶问题直接等于原问题的解（强对偶）
• 无论原始问题是否是凸的，对偶问题都是凸优化问题

显然，在某些情况下，直接对对偶问题求解可以得到原问题的解，而且对偶问题是凸优化，易于求解。所以利用对偶来求解是很有用的。

原始问题如下：

对偶问题如下：

原始问题和对偶问题的关系：

间隔最大化最优值求解

        求解间隔最大化最优值问题，就可应用拉格朗日对偶性，通过求解对偶问题得到原始问题的最优解。
对偶算法： 首先构建拉格朗日函数。对每个不等式约束引进拉格朗日乘子αi⩾0, i=1,2,…,N，定义拉格朗日函数：

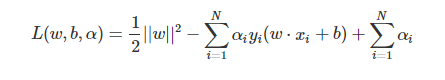
于是为了得到问题的解，就变成了先求L对w、b的极小，再求对α的极大。

参考资料：
从超平面到SVM（二）
拉格朗日乘子法和KKT条件
李航《统计学习方法》
石头的博客《图解KKT条件和拉格朗日乘子法》
瑞典皇家理工学院（KTH）“统计学习基础”课程的KKT课件
这门“统计学习基础”的schedule上有一些其它课件