支持向量机（SVM）详解（一）

支持向量机（SVM）详解（一）

第十三次写博客，本人数学基础不是太好，如果有幸能得到读者指正，感激不尽，希望能借此机会向大家学习。这一篇的部分内容来自于《机器学习》、《技法》，以及自己的一些见解。

预备知识：

这一部分首先介绍集合距离，然后定义“最优”分类器、间隔与支持向量，最后介绍二次规划问题以及回顾拉格朗日乘子法与对偶问题。关于拉格朗日乘子法与对偶问题的详细介绍可以参考我的上一篇博客《拉格朗日乘子法和对偶问题详解》。

点到超平面距离

　　假设存在超平面：$\omega^{T}\mathbf{x}+b=0$，而且点$\mathbf{x}_{a}$和$\mathbf{x}_{b}$在此超平面上，即

$$\begin{cases} \omega^{T}\mathbf{x}_{a}+b=0\\ \omega^{T}\mathbf{x}_{b}+b=0 \end{cases}$$ ，由此可知：
　　①　 $$\begin{cases} \omega^{T}\mathbf{x}_{a}+b=0\\ \omega^{T}\mathbf{x}_{b}+b=0 \end{cases}$$
　　②　 $\omega$是超平面的一个法向量，即 $\omega\perp\left(\mathbf{x}'-\mathbf{x}''\right)$
　　点 $\mathbf{x}$是超平面外的一点，那么点到超平面的距离可以表示为：

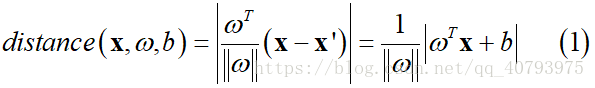
“最优”分类器

　　首先来看几幅不同分类边界的分类器效果图，每一个分类器都对4个样本点进行了正确分类：

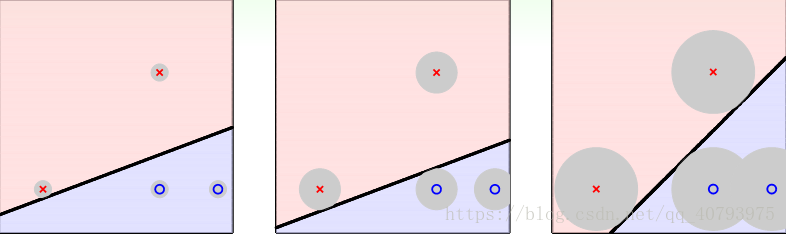
虽然每个分类器的正确分类率相同，但是当样本点存在一定的噪声时，分类器能否将其正确分类呢？或者，因为样本点数目的局限性而不能表现出整个训练集的数据分布特征时，分类器能否将新加入的样本点正确分类呢？这就体现除了分类器的鲁棒性（robust）和泛化性能的重要性，显然基于以上两点，最右边的分类器的性能最优。

间隔与支持向量

　　由【1】中的条件，我们可以使用$\omega^{T}\mathbf{x}+b$的大小来表示样本点$\mathbf{x}$有多大的可能性属于正（负）样本点集，即若$\omega^{T}\mathbf{x}+b=1$，那么样本有100%的可能性属于正样本集。
假设存在一个超平面可以将所有训练样本正确分类，即每个标记为+1的样本点均位于超平面的正样本点集的一侧，每个标记为-1的样本点均位于超平面的负样本点集的一侧，那么对于$\left(\mathbf{x}_{i},y_i\right)\in{D}$，均满足：

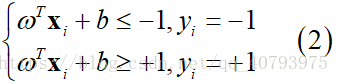
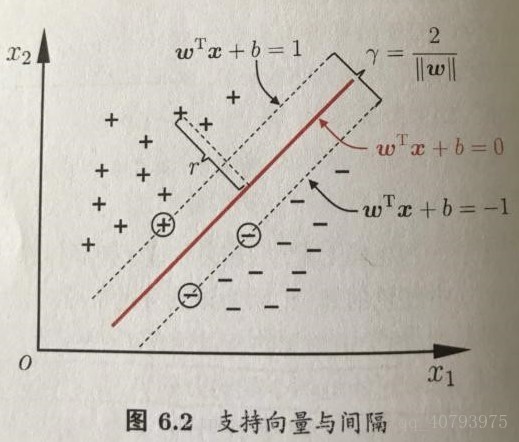
　　如下图所示，距离超平面最近的这几个样本点使得式（2）中的等式成立，这些点被称为“支持向量”，从之后的讨论可知，支持向量机最终生成的模型仅仅依赖于这些支持向量，这与线性感知机（PLA）中模型由被误分类的样本点决定类似，两个异类的支持向量之间的距离被称为“间隔”，由【1】中的距离公式可知：

其中$\mathbf{x}_i\in{D_{sv+}}$，$\mathbf{x}_i\in{D_{sv-}}$。

二次规划问题（Quadratic Programming Problem）

(1)（凸）二次规划问题的条件是：
　　① 优化目标是变量的（凸）二次目标函数；
　　② 约束条件是变量的线性不等式。
(2) 二次规划问题的描述格式如下所示

(3) 二次规划问题的求解步骤如下所示

(4) 根据实对称矩阵$Q$的不同，问题的解分为以下几种情况：
　　① $Q$为正定矩阵时，该问题存在唯一解；
　　② $Q$为非正定矩阵是，该问题是有多个局部极小点的NP-hard问题。

拉格朗日乘子法（Lagrange Multipliers）

　　拉格朗日乘子法是一种寻找多元函数在一组约束下的极值的方法，通过引入拉格朗日乘子，可以将$d$个变量的多元函数和$k$个约束条件的最优化问题转化为具有$d+k$个变量的无约束优化问题来进行求解。下面分别对不同情况进行讨论：
(1) 约束条件为等式约束
　　假设优化问题的目标优化函数为$f\left(\mathbf{x}\right)$，等式约束为$h_i\left(\mathbf{x}\right)$，例如

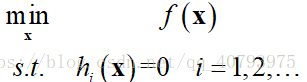
在这种情况下，拉格朗日函数可以定义为

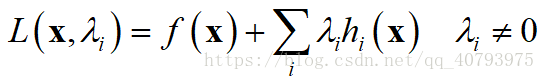
(2) 约束条件为不等式约束
　　假设优化问题的目标优化函数为$f\left(\mathbf{x}\right)$，不等式约束为$g_i\left(\mathbf{x}\right)$，例如

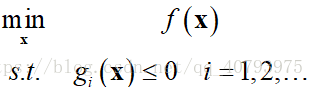
在这种情况下，拉格朗日函数可以定义为

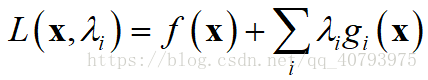
可以证明，不等式约束下的拉格朗日乘子法要满足KKT条件，即

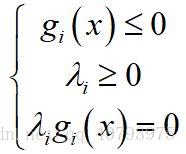
(3) 包含以上两种情况
　　假设优化问题的目标优化函数为$f\left(\mathbf{x}\right)$，等式约束为$h_i\left(\mathbf{x}\right)$，不等式约束为$g_if\left(\mathbf{x}\right)$，例如

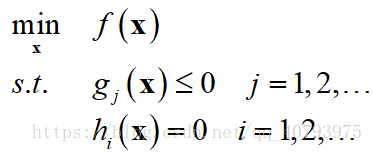
在这种情况下，拉格朗日函数可以定义为

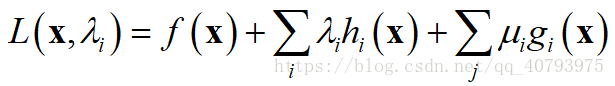
可以证明，这种情况下的拉格朗日乘子法要满足KKT条件，即

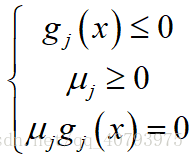
拉格朗日乘子法的推导过程详见《拉格朗日乘子法与对偶问题》。

对偶问题

　　对于【5】中的第三种情况，即

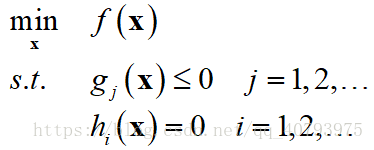
如果满足下列条件
　　① 目标优化函数是凸函数
　　② 变量所属集合是凸集合
或
　　① 目标函数是凸函数
　　② 变量的约束函数是凸函数（不等式约束时），或者是仿射函数（等式约束时）
那么，上述优化问题可以通过下式转化为其“强对偶问题”：

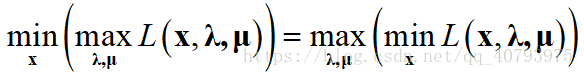
推导过程

支持向量机根据分类边界能否将全部样本点正确划分，可以分为“硬间隔”和“软间隔”两种类型，由于篇幅限制，这篇文章只涉及到“硬间隔”类型的支持向量机，关于“软间隔”类型支持向量机将在下一篇文章《支持向量机（SVM）详解（二）》中介绍到，有兴趣的读者可以持续关注。

一、“硬间隔”（Hard-margin）支持向量机

　　“硬间隔”支持向量机是一种满足式（2）的，可以将训练样本“完美”划分的分类器。

目标函数

　　这种分类器的训练目标是找到具有“最大间隔”（Max-margin）的划分超平面，即找到满足式（2）约束条件的最大的$margin\left(\omega,b\right)$，他的目标函数可以表示为

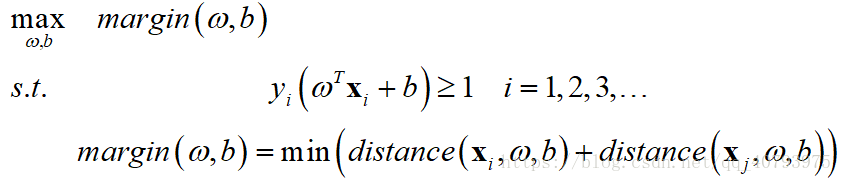
由式（1）和约束条件可知，

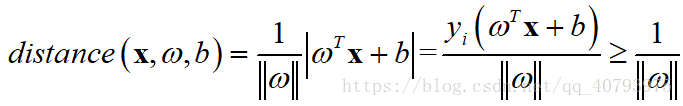
那么目标函数可以转化为

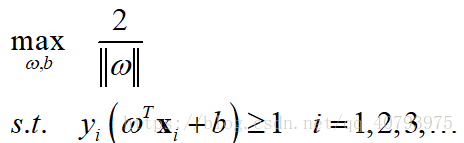
即

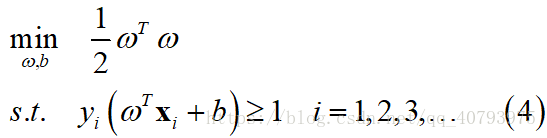
其中，$\omega^{T}\omega$可以看做是使用2-范数的平方对模型进行正则化，这就是硬间隔支持向量机的目标函数。

目标函数的对偶问题

　　由【4】可知，式（4）是凸二次优化问题，可以直接用现成的优化计算包进行求解，但是，当样本属性增加时，直接求解这类高维的二次优化问题的计算效率很低，因此，转为求其“对偶问题”（dual$\ $problem）。
　　首先，由【5】可知，

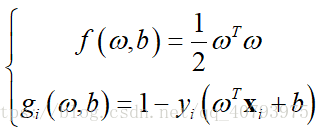
　　加入拉格朗日乘子$\alpha_i\geqslant{0}$后，该优化问题的拉格朗日乘子函数可以表示为

其KKT条件为

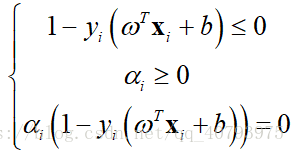
由SVM的优化目标和式（5）可知

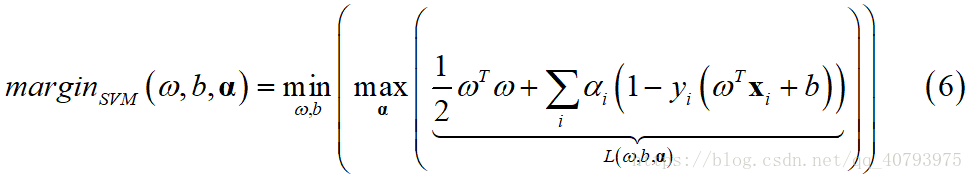
需要注意的是：
　　(1) 当存在样本点$\mathbf{x}$不满足式（2）的条件，即没有被正确分类，那么$\alpha\left(1-y\left(\omega^{T}\mathbf{x}+b\right)\right)\geqslant{0}$
这时$\underset{\alpha}{max}\left ( \frac{1}{2}\omega ^{T}\omega +\sum_{i}\alpha _{i} \left ( 1-y_{i}\left ( \omega ^{T}\mathbf{x}_{i}+b \right ) \right ) \right )\rightarrow +\infty$，优化结果变为$margin_{SVM}\left(\omega,b,\alpha\right)\rightarrow+\infty$；
　　(2) 而当所有的样本点均满足式（2），那么对于任意样本点$\mathbf{x}$，
$\alpha\left(1-y\left(\omega^{T}\mathbf{x}+b\right)\right)\leqslant{0}$
这时$\underset{\alpha}{max}\left ( \frac{1}{2}\omega ^{T}\omega +\sum_{i}\alpha _{i} \left ( 1-y_{i}\left ( \omega ^{T}\mathbf{x}_{i}+b \right ) \right ) \right )\rightarrow \frac{1}{2}\omega^{T}\omega$，优化结果变为
$margin_{SVM}\left(\omega,b,\alpha\right)\rightarrow\frac{1}{2}\omega^{T}\omega$；
　　其次，就要求解该优化问题的对偶问题。由于，$f\left(\omega,b\right)$和$h_i\left(\omega,b\right)$均为变量$\omega$、$b$的线性函数，他们对$\omega$、$b$的二阶偏导数均大于等于0，即这两个函数是凸函数。那么，式（6）的强对偶问题可以由【6】推出

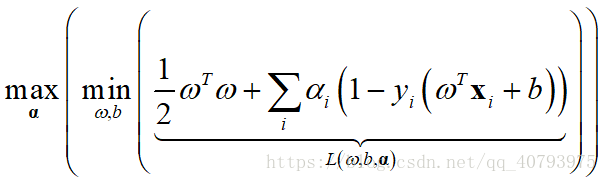
这时，使用求解拉格朗日乘子函数的一般解法对对偶问题进行求解。
① 分别求拉格朗日乘子函数对变量$\omega$、$b$的偏导数，并将他们置零：

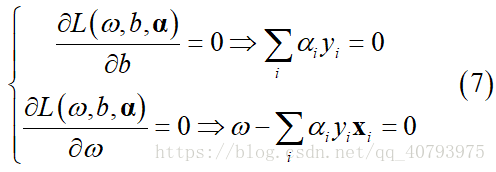
② 将以上关于$\omega$、$b$的等式带入对偶问题中，得到

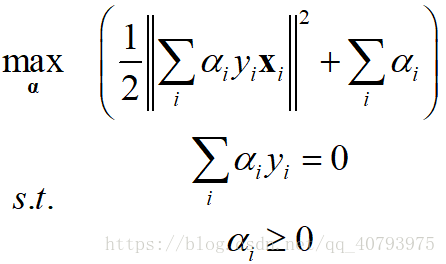
将式子中的平方项展开得到

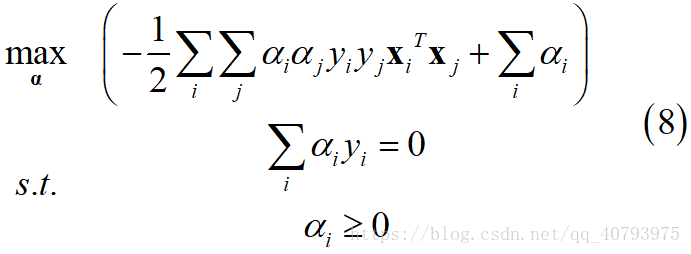
③ 可以看出式（8）是一个二次规划问题，可以使用现有的二次规划包进行求解，且这个对偶问题的维数为1，该问题的规模与训练样本数目有关，开销很大，因此一般使用SMO（Sequentia$\ $Minimal$\ $Optimization）算法对这个问题进行求解；
④ 得到参数$\alpha$后，可以根据式（7）求得参数$\omega$，由KKT条件中的$\alpha_i\left(1-y_i\left(\omega^{T}\mathbf{x}_i+b\right)\right)=0$可以得到参数$b$；
⑤ 在得到上述参数后，SVM的分类边界可以表示为

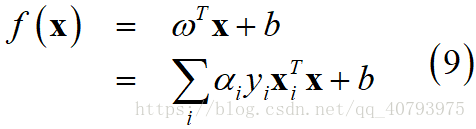
对KKT条件的理解

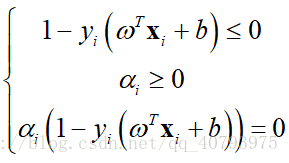
　　由$\alpha_i\left(1-y_i\left(\omega^{T}\mathbf{x}_i+b\right)\right)=0$可知，对于任何样本点$\left(\mathbf{x},y\right)$，总有$\alpha_i=0$或$1-y_i\left(\omega^{T}\mathbf{x}_i+b\right)=0$。当$\alpha_i=0$时，由式（9）可知，这个样本点对$f\left(\mathbf{x}\right)$没有影响；若$\alpha_i>0$，则必有$1-y_i\left(\omega^{T}\mathbf{x}_i+b\right)=0$，这个样本点位于最大间隔边界上，是一个支持向量。这表明，当SVM训练完成后，不需要保存所有的训练样本，最终模型只与支持向量有关。

---

由于在现实任务中很多情况下都不满足式（2）这种情况，为了避免使用核函数带来的过拟合问题，软间隔支持向量机允许训练集中的一部分样本不满足“完美”划分条件，但是在最大化间隔时，应使不满足约束的样本点尽可能少。有关于“软间隔”支持向量机和核函数的内容将在下一篇文章中进行介绍。