支持向量机详解之——系列1

支持向量机预备知识

一、深入理解超平面

        例1，下面是一个只有x轴的一维坐标轴，该轴同样存在原点，x轴正方向和x轴反方向，且该轴上分布了很多点：

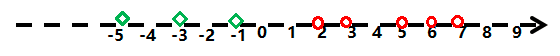
绿色的菱形坐标从左至右依次为：-5，-3，-1；红色的圈圈坐标从左到右依次为：2，3，5，6，7；此时，假如要求在坐标轴上找一个分割点，来分割红色的圆圈和绿色的菱形，而且要求只允许找一个点来分割这两部分样本，并且要求此点分割效果最好，如何去找呢？
答案是： 在闭区间 (-1,2) 直接任取一点都可以将这两部分样本分开，且只能取这里面的点，而找到一个最有分割点，我只需要取最近的两个点的中间点即可，使最有分割点至两边的距离都最远

        例2，上面是一维坐标下的情况，如果是二维直角坐标系情况，现在要在正类（A、B、C、D、E）与负类（F、G、H）之间找一条直线来将两类样本点分开，如下如所示这样的线存在多条，要求寻找到一条划分效果最好，如何做呢？

答案是： 先根据两点距离公式求两点之间的距离，经过计算得到了三对距离CF、CG、EG，那么此问题就转化为了在四个点C、E、F、G中找一条直线将两类样本效果最好的分开，只需在三对距离之间找到一个中点就好了，所以可以连线CF、CG、EG，找到它们的中点，然后连线，此问题解决。
简单来说，我们只需考虑两类距离最近的点分别到最优分割线的距离都最远即可。

        以上问题转化为支持向量机的核心问题：

• 通俗理解就是要在两类样本点之间找一条直线（超平面）来将两类样本点分开，存在多条划分直线（超平面），那么如何求得这些直线（超平面），并且选出使划分效果最好的，如何做呢？
  两类样本之间存在多条直线可以划分，对于此问题，只需要找到两个类中离得最近的样本点，再找到一条直线（超平面）使这些样本点同时最远即可，此时可以转化成数学问题。

• 该问题可以分两步进行解决：

• （1）找到两类样本之间最近的那一部分点（用距离公式，高维空间也适用）
  

• （2）找到一条直线（高维空间称之为超平面）使得（1）中最近的那些样本点到此直线（或超平面）的距离相等且尽量最大，此处可以用“点到直线（超平面）的距离”来解决，并且由于要把两类样本分开，所以必然一部分样本点在直线上方，一部分在直线下方，根据直线的规律可知（斜率大于0），若(x0,y0)在直线上方，则满足Ax0+By0+C>0，若（x0,y0）在直线下方，则满足Ax0+By0+C<0。

• 二维空间里面，一条直线的方程可以表示为：Ax+By+C=0

• 三维空间里面，平面的方程可以表示为：Ax+By+Cz+D=0

如果是更高维的数据呢？这时就需要引入超平面：

• 依次推广，n维空间的超平面方程可以表示为：
  w1x1+w2x2+w3x3+w4x4+…+wnxn+b=0
  此处用x1、x2、x3、…、xn来表示n维坐标系，各个维度的系数此处也可以用w1、w2、w3、…、wn来表示。
  
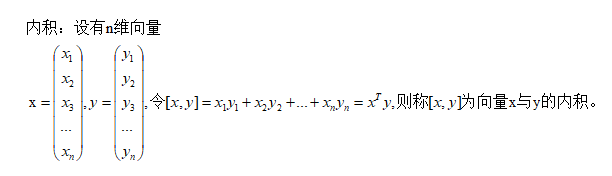
  可以将x看作w，y看作x，则上面超平面方程就变成了： [w,x]+b = 0 ，即： $w^Tx + b = 0$
  所以，样本空间中，任何一个超平面都可以用方程如下方程表示： $w^Tx + b = 0$
  其中，W=(w1,w2,w3,…,wn)为法向量，b为位移项，可认为是将平面平移到坐标原点所需距离（所以D=0时，平面过原点），该超平面可以唯一的由此方程决定。
• 为何该方程的法向量正好是该平面方程的变量系数呢？解释如下：
  

二、间隔最大化

        找到两类样本点之间离得最近的那一部分点（称之为支持向量），并将问题同样转化为找到中间一个超平面将这部分样本点划分开，此时又涉及到这些样本点到超平面的距离（即支持向量到超平面的距离），关于样本点到超平面的距离，可以如下去通俗的理解：
首先，点到平面的距离公式推导

再来看，点到超平面的距离：

        回顾完点到直线距离与点到超平面距离后，下面将着重介绍一下支持向量机中的 支持向量、间隔边界、函数间隔、几何间隔 等知识：

• 函数间隔
  一个点距离分离超平面的远近可以表示分类预测的确信程度，在分离超平面 $w^Tx + b = 0$确定的情况下， $|w^Tx + b |$表示点 x 到超平面的相对距离。通过观察 $w^Tx + b $ 和 y 是否同号来判断分类是否正确。所以可用 $y(w^Tx + b)$表示分类的正确性和确信度，这就是函数间隔：

  $\gamma^{&#x27;} = y(w^Tx + b)$

  对于训练集中m个样本点对应的m个函数间隔的最小值，就是整个训练集的函数间隔。

• 几何间隔
  函数间隔并不能正常反应点到超平面的距离，因为当分子成比例的增长时，分母也是成倍增长。为了统一度量，我们需要对法向量w加上约束条件，这样我们就得到了几何间隔定义为：

  $\gamma = \frac{y(w^Tx + b)}{||w||_2} = \frac{\gamma^{&#x27;}}{||w||_2}$

  几何间隔才是点到超平面的真正距离。

• 支持向量
          如下图所示，分离超平面为 $w^Tx + b = 0$，如果所有的样本不光可以被超平面分开，还和超平面保持一定的函数距离（下图函数距离为1），那么这样的分类超平面是最优的。可以证明，这样的超平面只有一个。和超平面平行的保持一定的函数距离的这两个超平面对应的向量，我们定义为支持向量，如下图虚线所示。（在线性可分情况下，训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量）
  

• 间隔边界
          $w^Tx + b = 1$与 $w^Tx + b = -1$平行，没有实例点落在中间，分离超平面 $w^Tx + b = 0$落在中间， $w^Tx + b = 1$与 $w^Tx + b = -1$称为间隔边界，它们之间的距离称为间隔。
  在决定分离超平面时只有支持向量起决定性作用，而其他实例并不起作用，所以将这种模型称为支持向量机。

• 间隔最大化
          支持向量机学习的基本思想就是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。间隔最大化直观解释：对训练数据集找到几何间隔最大的超平面。意味着以充分大的确信度对训练数据进行分类。最大间隔分离超平面可以表示为约束最优化问题：
  
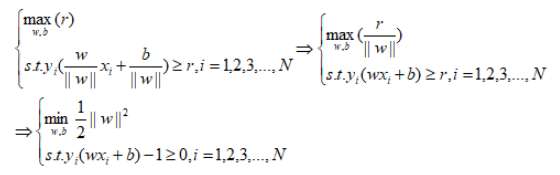
  上述公式第一部分就是几何间隔最大化，第二部分就是将第一步的几何间隔最大化转化为函数间隔最大化，第三部分可以这样理解：假设w=w0r，b=b0r，则推导以后 r 可以被消掉，即在优化过程中 r 的大小对优化并不产生影响，此时可以认为 w0 和 b0 认为就是 w 和 b，所以最终该问题就转化成了以下的数学最优化问题。
  
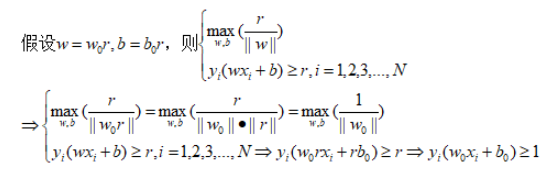
  由于 $\frac{1}{||w||_2}$的最大化等同于 $\frac{1}{2}||w||_2^2$的最小化。这样间隔最大化函数等价于：
  
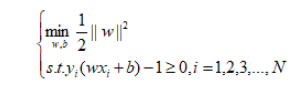
  到此，支持向量机的预备知识基本讲解完毕，如有错误欢迎大家指出，从下节将会深入介绍支持向量机原理，后面剩下基本就是纯数学推理和核函数部分了。

参考资料：
从超平面到SVM（一）
李航《统计学习方法》