【逻辑回归】—— Logistic回归原理小结

逻辑回归：Logistic Regression(LR)

       逻辑回归是一个经典的分类算法，并不是一个回归算法，它可以处理二元分类以及多元分类，个人认为由于逻辑回归的原理是由回归模型的演变而来的，因此含有“回归”二字，而逻辑回归与线性回归同属于广义线性模型种的一类。

广义线性模型分类：
根据因变量不同，常分为以下几类：

• 因变量是连续的：多元线性回归
• 因变量是二项分布：Logistic回归
• 因变量是Poission分布：Poission回归
• 因变量是负二项分布：负二项回归

1. 从线性回归到Logistic回归

       线性回归模型是求出输出变量 Y 和输入特征变量 X 之间的线性关系系数 θ，使其满足 Y = Xθ ，这里的 Y是连续型的，如果想要使 Y 是离散型的（分类变量），那么就需要对 Y 进行一次函数变换（映射 : g），得到的 g(Y)，使得当 g(Y) 值在某个实数区间时样本的输出值为一类别，而当在另一个实数区间时对应样本的输出值为另一类别，当只有两个类别时，就得到了一个二分类模型，我们就从线性模型过度到了Logistic回归模型。

Logistic回归的具体由来：
       Logistic回归是通过固有的logistic函数估计概率来衡量因变量和一个或多个自变量之间的关系，logistic函数也称为Sigmod函数，是一个S型曲线，它可以将任意实数值映射到（0,1）之间的值，然后用阈值分类器将0与1之间的值转换为分类变量。

• Logistic函数（或称为Sigmoid函数），函数形式为：
  $g(z) = \frac{1} {1+e^{-z}}$
  
• 由线性回归模型引出Logistic回归分类模型示意图：
  

2. 二元Logistic回归模型常规步骤：

• 寻找二元LR回归模型的预测函数 $h_{\theta}(x)$
• 构造二元LR回归模型的损失函数 $J(\theta)$
• 采用一定的算法求取回归参数 θ 使 $J(\theta)$ 函数取得最小值

2.1 寻找预测函数： $h_{\theta}(x)$

• Sigmod函数（单调可微函数）： $g(z) = \frac{1} {1+e^{-z}}$
  • Sigmod函数性质：
    
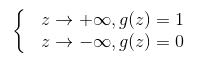
  • Sigmod函数导数性质： $g^{'}(z) = g(z)(1-g(z))$
• 令 g(z) 中的 z 为：z = xθ，这样就得到了二元Logistic回归模型的一般形式：
  • $h_{\theta}(x) = \frac{1} {1+e^{-x\theta}}$
  • 假设：
    
• Logistic回归模型的矩阵形式：
  • $h_{\theta}(X) = \frac{1}{1+e^{-X\theta}}$
    • $h_{\theta}(X)$为模型输出值，mx1维向量；
    • X为样本特征矩阵，mxn维矩阵；
    • $\theta$为模型参数，nx1维向量；

2.2 构造损失函数： $J(\theta)$

        二元LR回归模型的预测函数建立好了，那么下面需要考虑采用什么方法来构建损失函数？这里我们采用常用的最大似然法来推导出损失函数。

• 假设我们的样本输出是0或者1两类，有：
  $P(y=1|x,\theta ) = h_{\theta}(x)$
  $P(y=0|x,\theta ) = 1- h_{\theta}(x)$

  那么由上节假设及上式，我们可以得到y的概率分布函数：

  $P(y|x,\theta ) = h_{\theta}(x)^y(1-h_{\theta}(x))^{1-y}$

• 下面就可以用最大似然函数法来求解模型系数θ，似然函数的代数表达式为：

• $L(\theta) = \prod\limits_{i=1}^{m}(h_{\theta}(x_{i}))^{y_{i}}(1-h_{\theta}(x_{i}))^{1-y_{i}}$

  其中m为样本的个数。

• 对似然函数取对数后就得到损失函数表达式，为方便后面优化操作，这里再对损失函数进行取反得：
  $J(\theta) = -logL(\theta) = -\sum\limits_{i=1}^{m}(y_{i}log(h_{\theta}(x_{i}))+ (1-y_{i})log(1-h_{\theta}(x_{i})))$

• 损失函数用矩阵法表示为：

  $J(\theta) = -Y^T\bullet logh_{\theta}(X) - (E-Y)^T\bullet log(E-h_{\theta}(X))$

  其中E为全1单位向量。

2.3 损失函数的优化方法：梯度下降法

        我们构造好完模型的损失函数后，下面的目标是极小化损失函数来得到对应的模型系数θ，得到最终的模型。
        对于二元Logistic回归的损失函数最常见的优化方法有：梯度下降法，坐标轴下降法，等牛顿法等。这里采用梯度下降法来推导出θ每次迭代的公式。由于代数法推导比较的繁琐，这里采用矩阵法推导二元Logistic回归梯度的过程。

• 对损失函数求θ的偏导过程：
  $\frac{\partial}{\partial \theta }J(\theta ) = [-Y \cdot \frac{1}{h_{\theta }(X)} \cdot h_{\theta }(X) \cdot (E- h_{\theta }(X)) \cdot \frac{\partial}{\partial \theta }(X\theta )] +[(E-Y) \cdot \frac{1}{E-h_{\theta }(X)} \cdot h_{\theta }(X) \cdot (E- h_{\theta }(X)) \cdot \frac{\partial}{\partial \theta }(X\theta )]$

  $\frac{\partial}{\partial \theta }J(\theta ) = [-Y \cdot \frac{1}{h_{\theta }(X)} \cdot h_{\theta }(X) \cdot (E- h_{\theta }(X)) \cdot X^{T}] +[(E-Y) \cdot \frac{1}{E-h_{\theta }(X)} \cdot h_{\theta }(X) \cdot (E- h_{\theta }(X)) \cdot X^{T}]$

  $\frac{\partial}{\partial \theta }J(\theta ) = [-Y \cdot (E- h_{\theta }(X)) \cdot X^{T}]+[(E-Y) \cdot h_{\theta }(X) \cdot X^{T}]$

  $\frac{\partial}{\partial \theta }J(\theta ) = -Y \cdot E \cdot X^{T}+Y \cdot h_{\theta }(X) \cdot X^{T}+E \cdot h_{\theta }(X) \cdot X^{T}-Y \cdot h_{\theta }(X) \cdot X^{T}$

  $\frac{\partial}{\partial \theta }J(\theta ) = -Y \cdot E \cdot X^{T} + E \cdot h_{\theta }(X) \cdot X^{T}$

  对于刚才的求导公式我们进行化简可得：

  $\frac{\partial}{\partial \theta }J(\theta ) = X^{T}\cdot (h_{\theta }(X)-Y)$

• 每一步向量θ的迭代公式如下：

  $\theta = \theta - \alpha \cdot \frac{\partial}{\partial \theta }J(\theta )$

  $\theta = \theta - \alpha \cdot X^T(h_{\theta}(X) - Y )$

• 常用矩阵求导公式及向量求导的链式法则：
  $\frac{\partial}{\partial B }(AB ) = A^{T}$

  $\frac{\partial}{\partial A }(A^{T}B ) = B$

  $\frac{\partial}{\partial X }(X^{T}AX ) = 2AX$

  $\frac{\partial}{\partial z}g(z) = g(z)(1-g(z))$

  $\frac{\partial}{\partial \theta }g(X\theta ) = g(X\theta)(1-g(X\theta))\cdot \frac{\partial}{\partial \theta }(X\theta )=g(X\theta)(1-g(X\theta))\cdot X^{T}$

3. Logistic回归的优缺点：

• 优点：
  • （1）速度快，适合二分类问题，不需要缩放输入特征；
  • （2）简单易理解，直接可以得到各特征的权重；
  • （3）易更新模型吸收新数据
• 缺点：
  • （1）不能同Logistic回归去解决非线性问题，因为Logistic的决策面试线性的；
  • （2）高度依赖正确的数据表示；
  • （3）对多重共线性数据较为敏感；

4. Logistic回归与线性回归的区别：

最大区别在于它们的因变量不同，Logistic回归与现行回归属于同一家族：广义线性模型。

• （1）线性回归要求变量服从正态分布，Logistic回归对变量分布无要求；
• （2）线性回归要求因变量是连续型的，Logistic回归要求因变量是分类变量；
• （3）线性回归要求自变量和因变量呈线性关系，Logistic并不要求；
• （4）Logistic回归是分析因变量取某个值的概率与自变量的关系，而线性回归是直接分析因变量与自变量的关系；

5. Logistic回归算法Python实现

5.1 Logistic Regression in Python

from math import exp
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 载入数据集，查看数据
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = [
        'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
    ]
    data = np.array(df.iloc[:100, [0, 1, -1]])
    return data[:, :2], data[:, -1]  # 选取特征集、类别集

# 初始化数据集
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
X_train[0:5], y_train[0:5]

(array([[6.3, 3.3], [5.5, 3.5], [5.8, 4. ], [6. , 2.2],[4.8, 3.4]]),
array([1., 0., 0., 1., 0.]))

class LRClassifier:
    # 初始化最大迭代数及学习步长
    def __init__(self, max_iter=200, learning_rate=0.01):
        self.max_iter = max_iter
        self.learning_rate = learning_rate

    # 构建sigmod函数
    def sigmod(self, x):
        return 1 / (1 + np.exp(-x))

    def data_matrix(self, X):
        data_mat = []
        for d in X:
            data_mat.append([1.0, *d])
        return data_mat

    # 训练LR模型
    def fit(self, X, y):
        data_mat = self.data_matrix(X)
        self.weights = np.zeros((len(data_mat[0]), 1),
                                dtype=np.float32)  # 初始化权重系数为0为0

        for iter_ in range(self.max_iter):
            for i in range(len(X)):
                # 计算概率值
                result = self.sigmod(np.dot(data_mat[i], self.weights))
                error = y[i] - result
                # 更新权重0
                self.weights += self.learning_rate * error * np.transpose(
                    [data_mat[i]])
            print('Logistic回归模型(学习步长={}，迭代次数={}，更新权重为={})'.format(
                self.learning_rate, iter_ + 1, self.weights))

    # 计算测试集正确率
    def score(self, X_test, y_test):
        right = 0
        X_test = self.data_matrix(X_test)
        for x, y in zip(X_test, y_test):
            result = np.dot(x, self.weights)
            if (result > 0 and y == 1) or (result < 0 and y == 0):
                right += 1
        return right / len(X_test)

lr_clf = LRClassifier()
lr_clf.fit(X_train, y_train)
lr_clf.score(X_test, y_test)

Logistic回归模型(学习步长=0.01，迭代次数=1，更新权重为=[[-0.02205414]
[ 0.04048975]
[-0.18022126]])
Logistic回归模型(学习步长=0.01，迭代次数=2，更新权重为=[[-0.03481127]
[ 0.12593015]
[-0.32383457]])
Logistic回归模型(学习步长=0.01，迭代次数=3，更新权重为=[[-0.04712692]
[ 0.20664313]
…
Logistic回归模型(学习步长=0.01，迭代次数=200，更新权重为=[[-0.9994935]
[ 3.3933694]
[-5.6629505]])

1.0

# 绘制决策面
x_ponits = np.arange(4, 8)
y_ = -(lr_clf.weights[1]*x_ponits + lr_clf.weights[0])/lr_clf.weights[2]
plt.plot(x_ponits, y_)

# 绘制样本点
plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.legend()

5.2 Logistic Regression in sklearn

sklearn.linear_model中与逻辑回归有关的主要是3个类：

• LogisticRegression
• LogisticRegressionCV
• logistic_regression_path
  其中LogisticRegression和LogisticRegressionCV的主要区别：LogisticRegressionCV使用了交叉验证来选择正则化系数C。而LogisticRegression需要自己每次指定一个正则化系数。而logistic_regression_path类则比较特殊，它拟合数据后，不能直接来做预测，只能为拟合数据选择合适逻辑回归的系数和正则化系数。主要是用在模型选择的时候。

from sklearn.linear_model import LogisticRegression

clf = LogisticRegression(max_iter=200)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
print(clf.coef_, clf.intercept_)

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=200, multi_class=‘ovr’, n_jobs=1,
penalty=‘l2’, random_state=None, solver=‘liblinear’, tol=0.0001,
verbose=0, warm_start=False)

1.0

[[ 1.91865915 -3.20636409]] [-0.51918926]

x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)

plt.plot(X[:50, 0], X[:50, 1], 'bo', color='blue', label='0')
plt.plot(X[50:, 0], X[50:, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

常用参数说明：

• （1）penalty：正则化选择参数

  • penalty参数可选择的值为"l1"和"l2"，分别对应L1的正则化和L2的正则化，默认是L2的正则化

• （2）solver：优化算法选择参数，决定了对逻辑回归损失函数的优化方法，有四种算法分别是：

  • liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。

  • lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵，即：海森矩阵来迭代优化损失函数。

  • newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵，即：海森矩阵来迭代优化损失函数。

  • sag：随机平均梯度下降，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。

• （3）multi_class：分类方式选择参数

  • multi_class参数决定了我们分类方式的选择，有 ovr和multinomial两个值可以选择，默认是 ovr，如果是二元逻辑回归，ovr和multinomial并没有任何区别。

  • ovr：one-vs-rest(OvR)，对于第K类的分类决策，把所有第K类的样本作为正例，除第K类样本外的所有样本都作为负例，然后做二元逻辑回归，得到第K类的分类模型。其他类的分类模型获得以此类推。

  • multinomial：many-vs-many(MvM)，特例one-vs-one(OvO)，如果模型有T类，我们每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，进行二元逻辑回归，得到模型参数。我们一共需要T(T-1)/2次分类。

  • 如果选择ovr，则4种损失函数的优化方法都可以选择。但是如果选择了multinomial,则只能选择newton-cg, lbfgs和sag。

• （4）class_weight：类型权重参数

  • class_weight参数用于标示分类模型中各种类型的权重，可以不输入即所有类型的权重一样。也可以选择balanced让类库自己计算类型权重，或者自己输入各个类型的权重，比如对于0,1的二元模型，我们可以定义class_weight={0:0.9, 1:0.1}。

• （5）sample_weight：样本权重参数

  • sample_weight来自己调节每个样本权重。

• （6）max_iter：最大迭代次数

       逻辑回归原理是实现就介绍到这里，欢迎批评指正，针对多元Logistic回归模型这里没有做过多的介绍，后期归纳总结后再做补充。
转载请注明出处

参考资料：
李航《统计学习方法》
代码部分转自“机器学习初学者”作者内容
逻辑回归原理及公式推导