Logistic回归小结

首先要清楚，逻辑回归是一种分类算法。它是在线性回归模型的基础上，使用Sigmoid函数，将线性模型的预测结果转变为离散变量，从而用于处理分类问题。

1 逻辑回归原理

以二分类为例，说明逻辑回归的工作原理。由线性回归小结基础，不难得出线性回归的假设函数\(h_{\theta }^{'}\left ( x \right )\)，在逻辑回归中，使用Sigmoid函数使得\(h_{\theta }^{'}\left ( x \right )\)的值在[0,1]区间内。
一般Sigmoid函数表示为：
\[g\left ( z \right )=\frac{1}{1+e^{-z}}\]

绘图展示Sigmoid函数：

#Sigmoid function
from scipy.special import expit

def sigmoid(z):    
    return 1/(1 +np.exp(-z))


def h(theta, X):
    return expit(np.dot(X, theta))


#check sigmoid function
myx = np.arange(-10, 10, 0.01)
plt.plot(myx, expit(myx))
plt.title('Sigmoid Function')
plt.show()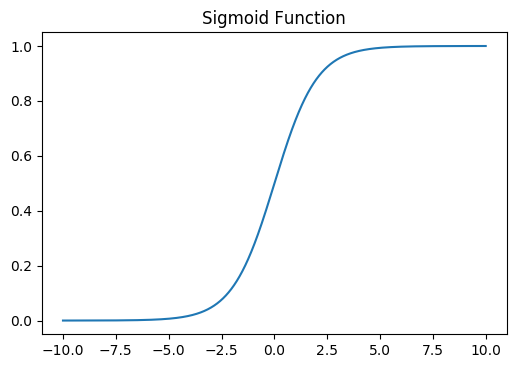

可以看到,Sigmoid函数当\(z\)趋于正无穷时，\(g\left ( z \right )\)趋于1，当\(z\)趋于负无穷时，\(g\left ( z \right )\)趋于0。
对于逻辑回归，令\(z=h_{\theta }^{'}\left ( x \right )\)，则有\(g\left ( z \right )=g\left ( h_{\theta }^{'}\left ( x \right ) \right )=\frac{1}{1+e^{-h_{\theta }^{'}\left ( x \right )}}\)，其中，$h_{\theta }^{'}\left ( x \right )=x\theta $，而 \(g\left ( z \right )\)。因此，逻辑回归的模型为：
\[h_{\theta }\left ( x \right )=\frac{1}{1+e^{-x\theta }}\]
结合Sigmoid函数，理解逻辑回归模型如何实现分类问题的。此时，\(h_{\theta }\left ( x \right )\)为模型输出，把它当作某一分类的概率值，赋予其概率含义。当\(h_{\theta }\left ( x \right )>0.5\)时，\(x\theta >0\)，则\(y\)为1，当\(h_{\theta }\left ( x \right )<0.5\)时，\(x\theta <0\)，则\(y\)为0，如此实现了分类问题。
逻辑回归模型的矩阵形式为：
\[h_{\theta }\left ( X \right )=\frac{1}{1+e^{-X\theta }}\]

因此，\(y\)取1的概率等于\(h_{\theta }\left ( x \right )\)，取0的概率为\(1-h_{\theta }\left ( x \right )\)，即：
\[p\left ( y|x;\theta \right )=h_{\theta }\left ( x \right )^{y}\left ( 1-h_{\theta }\left ( x \right ) \right )^{1-y}\]
似然函数:
\[L\left ( \theta \right )=p(y|x;\theta )=\prod_{i=1}^{m}P(y^{(i)}|x^{(i)};\theta )=\prod_{i=1}^{m}h_{\theta }(x^{(i)})^{y(i)}(1-h_{\theta }(x^{(i)}))^{1-y^{(i)}}\]
对数似然函数：
\[l(\theta )=logL(\theta )=\sum_{i=1}^{m}y^{(i)}logh_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))\]
损失函数：
\[J(\theta )=-logL(\theta )=-\sum_{i=1}^{m}(y^{(i)}logh_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)})))\]
损失函数的矩阵形式为:
\[J(\theta )=-Y^{T}logh_{\theta }(X)-(E-Y)^{T}log(E-h_{\theta }(X))\]
逻辑回归的优化目标：
\[\min_{\theta}J\left ( \theta \right )\]

2 逻辑回归算法

由于\(\frac{\partial J(\theta )}{\partial \theta }=X^{T}(h_{\theta }(X)-Y)\)
梯度下降法中$\theta $的迭代公式为:
\[\theta =\theta -\alpha \frac{\partial J(\theta )}{\partial \theta }=\theta -\alpha X^{T}(h_{\theta }(X)-Y)\]

3 逻辑回归代码实现

3.1 训练算法：使用梯度上升找到最佳参数

#Logistic 回归梯度上升优化算法
from numpy import *
def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(inX):
    return 1.0/(1+exp(-inX))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    m,n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = (labelMat - h)
        weights = weights + alpha*dataMatrix.transpose()*error
    return weights

dataArr, labelMat = loadDataSet()
print(gradAscent(dataArr, labelMat))
#输出
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]

4.2 分析数据：画出决策边界

#画出数据集和Logistic回归最佳拟合直线的函数
#绘制图像
import matplotlib.pyplot as plt
def plotBestFit(wei):
    weights = wei.getA()
    dataMat,labelMat=loadDataSet()
    dataArr=array(dataMat)
    n=shape(dataMat)[0]          #样本数目
    xcord1=[]; ycord1=[]
    xcord2=[]; ycord2=[]
    for i in range(n):
        if int(labelMat[i])==1:
            xcord1.append(dataArr[i,1])
            ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1])
            ycord2.append(dataArr[i,2])
    fig=plt.figure()
    ax=fig.add_subplot(111)
    ax.scatter(xcord1,ycord1,s=20,c='r',marker='s')
    ax.scatter(xcord2,ycord2,s=20,c='g')
    x = arange(-3.0, 3.0, 0.1)  # 直线x坐标的取值范围
    y = (-weights[0] - weights[1] * x) / weights[2]  # 直线方程
    plt.title('DataSet')
    ax.plot(x, y)
    plt.xlabel('X1');
    plt.ylabel('X2');
    plt.show()

dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
plotBestFit(weights)

梯度上升算法在500次迭代后得到的Logistic回归最佳拟合直线：

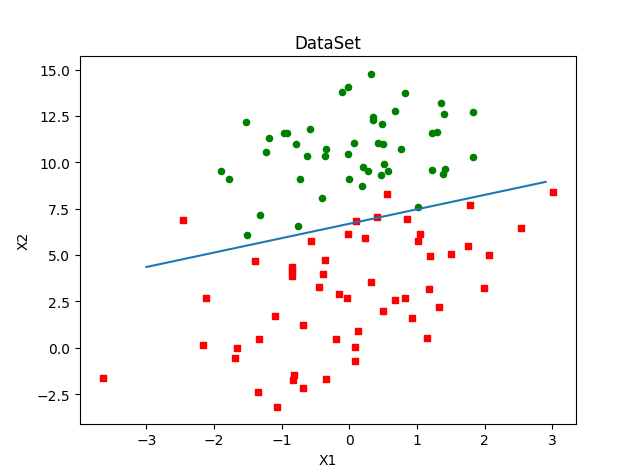
4.3 训练算法：随机梯度上升

梯度上升算法在每次更新回归系数时都需要遍历整个数据集，该方法在处理100个左右的数据集时尚可，但如果有数十亿样本和成千上万的特征，那么该方法的计算复杂度就太高了。一种改进方法是一次仅用一个样本点来更新回归系数，该方法称为随机梯度上升算法。

#随机梯度上升算法
def stocGradAscent0(dataMatrix, classLabels):
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha*error*dataMatrix[i]
    return weights

def plotBestFit(wei):
    
    dataMat,labelMat=loadDataSet()
    dataArr=array(dataMat)
    n=shape(dataMat)[0]          #样本数目
    xcord1=[]; ycord1=[]
    xcord2=[]; ycord2=[]
    for i in range(n):
        if int(labelMat[i])==1:
            xcord1.append(dataArr[i,1])
            ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1])
            ycord2.append(dataArr[i,2])
    fig=plt.figure()
    ax=fig.add_subplot(111)
    ax.scatter(xcord1,ycord1,s=20,c='r',marker='s')
    ax.scatter(xcord2,ycord2,s=20,c='g')
    x = arange(-3.0, 3.0, 0.1)  # 直线x坐标的取值范围
    y = (-weights[0] - weights[1] * x) / weights[2]  # 直线方程
    plt.title('DataSet')
    ax.plot(x, y)
    plt.xlabel('X1');
    plt.ylabel('X2');
    plt.show()

dataMat, labelMat = loadDataSet()
weights = stocGradAscent0(array(dataMat), labelMat)
plotBestFit(weights)

分类器错分了三分之一的样本:

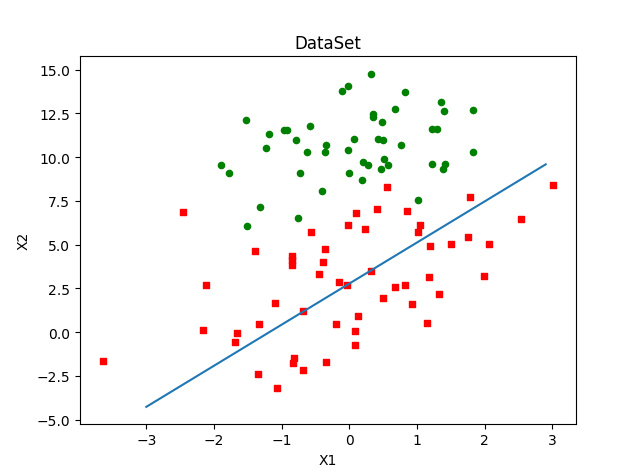
直接比较随机梯度上升和梯度上升的代码结果是不公平的，后者的结果是在整个数据集上迭代了500次才得到的。一个判断优化算法优劣的可靠方法是看它是否收敛，也就是说参数是否达到了稳定值，是否还会不断地变化？对此，我们在程序清单5-3中随机梯度上升算法上做了些修改，使其在整个数据集上运行200次。最终绘制的三个回归系数的变化情况

#调整梯度上升和随机梯度上升函数
def gradAscent(dataMatIn,classlabels):
    dataMatrix=mat(dataMatIn)
    labelMat=mat(classlabels).T
    m,n=shape(dataMatrix)
    alpha=0.01
    maxCycles=500
    weights=ones((n,1))
    weights_array=array([])
    for k in range(maxCycles):
        h=sigmoid(dataMatrix*weights)
        error=labelMat-h
        weights=weights+alpha*dataMatrix.T*error
        weights_array=append(weights_array,weights)    #一行
    weights_array=weights_array.reshape(maxCycles,n)
    return weights.getA(),weights_array

def stocGradAscent1(dataMatrix,classLabels,numIter=150):
    m,n=shape(dataMatrix)
    weights=ones(n)
    weights_array=array([])
    for j in range(numIter):
        dataIndex=list(range(m))
        for i in range(m):
            alpha=4/(1.0+j+i)+0.01
            randIndex=int(random.uniform(0,len(dataIndex)))
            h=sigmoid(sum(dataMatrix[randIndex]*weights))
            error=classLabels[randIndex]-h
            weights=weights+alpha*error*dataMatrix[randIndex]
            weights_array=append(weights_array,weights,axis=0)
            del(dataIndex[randIndex])
    weights_array=weights_array.reshape(numIter*m,n)
    return weights,weights_array

#绘制回归系数与迭代次数的关系
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
def plotWeights(weights_array1,weights_array2):
    #画布分成三行两列
    fig,axs=plt.subplots(nrows=3,ncols=2,sharex=False,sharey=False,figsize=(20,10))
    x1=arange(0,len(weights_array1),1)
    #绘制w0与迭代次数的关系
    axs[0][0].plot(x1,weights_array1[:,0])
    axs0_title_text=axs[0][0].set_title('梯度上升算法：回归系数与迭代次数关系')
    axs0_ylabel_text=axs[0][0].set_ylabel('W0')
    plt.setp(axs0_title_text,size=20,weight='bold',color='black')
    plt.setp(axs0_ylabel_text,size=20,weight='bold',color='black')
    #绘制w1与迭代次数关系
    axs[1][0].plot(x1,weights_array1[:,1])
    axs1_ylabel_text=axs[1][0].set_ylabel('W1')
    plt.setp(axs1_ylabel_text,size=20,weight='bold',color='black')
    #绘制w2与迭代次数关系
    axs[2][0].plot(x1,weights_array1[:,2])
    axs2_xlabel_text=axs[2][0].set_title('迭代次数')
    axs2_ylabel_text=axs[2][0].set_ylabel('W2')
    plt.setp(axs2_xlabel_text,size=20,weight='bold',color='black')
    plt.setp(axs2_ylabel_text,size=20,weight='bold',color='black')

    x2=arange(0,len(weights_array2),1)
    #绘制w0与迭代次数关系
    axs[0][1].plot(x2,weights_array2[:,0])
    axs0_title_text=axs[0][1].set_title('随机梯度上升算法：回归系数与迭代次数关系')
    axs0_ylabel_text=axs[0][1].set_ylabel('W0')
    plt.setp(axs0_title_text,size=20,weight='bold',color='black')
    plt.setp(axs0_ylabel_text,size=20,weight='bold',color='black')
    #绘制w1与迭代次数关系
    axs[1][1].plot(x2,weights_array2[:,1])
    axs1_ylabel_text=axs[1][1].set_ylabel('W1')
    plt.setp(axs1_ylabel_text,size=20,weight='bold',color='black')
    #绘制w2与迭代次数关系
    axs[2][1].plot(x2,weights_array2[:,2])
    axs2_xlabel_text=axs[2][1].set_title('迭代次数')
    axs2_ylabel_text=axs[2][1].set_ylabel('W2')
    plt.setp(axs2_xlabel_text,size=20,weight='bold',color='black')
    plt.setp(axs2_ylabel_text,size=20,weight='bold',color='black')

    plt.show()

# 绘图
dataMat, labelMat = loadDataSet()
weights1, weights_array1 = gradAscent(dataMat, labelMat)
weights2, weights_array2 = stocGradAscent1(array(dataMat), labelMat)
plotWeights(weights_array1, weights_array2)

#改进的随机梯度上升算法
import random

def stocGradAscent1(dataMatrix,classLabels,numIter=150):
    m,n=shape(dataMatrix)
    weights=ones(n)
    for j in range(numIter):
        dataIndex=list(range(m))
        for i in range(m):
            alpha=4/(1.0+j+i)+0.01            #每次调整alpha值
            randIndex=int(random.uniform(0,len(dataIndex))) #随机选取样本，可以减少周期性波动
            h=sigmoid(sum(dataMatrix[randIndex]*weights))   #梯度上升这里是向量，随机梯度上升数据类型都是数值
            error=classLabels[randIndex]-h
            weights=weights+alpha*error*dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

dataMat, labelMat = loadDataSet()
weights = stocGradAscent1(array(dataMat), labelMat)
plotBestFit(weights)