ML————朴素贝叶斯原理和SKlearn相关库

二师兄养成记正式开始，以后就写这了。

写的不对的、有疑问的，恳请大佬指出来。

一. 贝叶斯定理

1. 条件概率：

P（A | B） = P(A B) / P（B） = P（A U B）/ P（B），表示 A在B条件下发生的概率= AB共同发生的概率 / B 发生的概率。

2. 贝叶斯定理：

已知 A在B条件下发生的概率 P（A | B）， B发生的概率P（B），求 P（B | A）发生的概率。

贝叶斯定理如下：

P（B | A） = P(A | B) P(B) / P(A)

二. NaiveBayes 算法

朴素贝叶斯之所以朴素，是有假设前提条件的：假设每个特征之前相互独立，那么联合概率：

P（A B） = P（A）P(B)

假设 A事件可以完全切分为{ A1，A2，...., An｝（全概率公式）

P（A1,A2,A3,...,An | B） = P(A1 | B) P(A2 | B) P(A3 | B) ... P(An | B)

那么NaiveBayes模型可以表示为：

P（B | A1,A2,A3, ... , An）= P(A1,A2,A3,...,An | B) P(B) / P(A1,A2,A3,...,An) P(A1,A2,A3,...,An | B) 又称后验概率

在各特征完全独立的情况下，则为：

P（B | A1,A2,A3, ... , An） = P(A1 | B) P(A2 | B) P(A3 | B) ... P(An | B) * P(B）/ P(A1)P（A2）...P(An)

在机器学习里，我们可以将上式的A1, A2至 An认为数据集的特征，B（｛B1，B2,..., Bn｝）为类标签。

那么 P（B | A1，A2，A3，...,An）可以表示为在A1,至An的特征条件下，类别为B的概率。

但是很难统计这个多条件下的条件概率，所以Bayes定理就是解决这个问题的。

Bayes 分类器就是求得最大后验概率 P(A1,A2,A3,...,An | B)，来估计P(B）和 P（Ai | B），因为 P(A1,A2,A3,...,An) 和P(B) 在训练数据给定时就已经是不变的常数。

Machine Learning 里常用 X1，X2，X3， ... , Xi 表示特征， Y1，Y2，...,Yj表示类标签, 所以朴素贝叶斯算法的公式可以表示为：

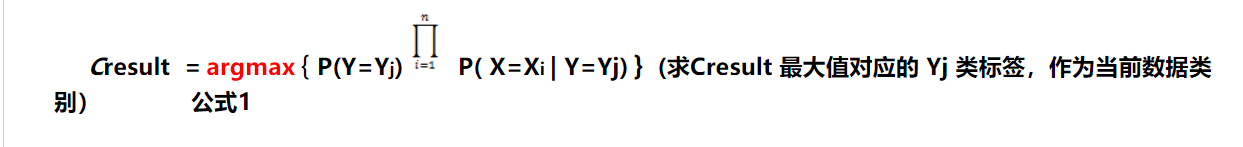
三. 参数估计

上述介绍了只需要求出P(A1 | B) P(A2 | B) P(A3 | B) ... P(An | B) ，就可以求得朴素贝叶斯计算结果.

假设类标签B有3个值： B1，B2和B3，

但具体怎么求 P（B1）是个问题，所以采用极大似然估计法，以分类样本中B1占比（频率代替概率）来估计B1的概率： P（B1） = Count（B1） / Sum(Bi)

对于上面公式1 中 P(Y=Yj) 可以使用极大似然估计求得，但P( X=Xi | Y=Yj) 如何求，那要根据特征Xi的分布确定：

① 若Xi为离散值，假设Xi符合多项式分布，那么P( X=Xi | Y=Yj)就是 Xi在 Yi类中出现的频率：

（Sklearn教程的解释）

② 若Xi为稀疏离散值值，可以假设Xi满足伯努利分布，可以使用伯努利分布公式求得P( X=Xi | Y=Yj)：

③ 若 Xi为连续值，假设Xi服从正态分布，那么可以使用正态分布式子求得P( X=Xi | Y=Yj)：

四. 实例解释朴素贝叶斯的执行过程（特征值都为离散值）

这是一个什么自然条件下打网球的训练数据（维度：14行×5列）：

四个特征为天气、温度、湿度和风强

标签：Yes：打网球，No：不打。

Day	Outlook	Temperature	Humidity	Wind	PlayTennis
D1	Sunny	Hot	High	Weak	No
D2	Sunny	Hot	High	Strong	No
D3	Overcast	Hot	High	Weak	Yes 1
D4	Rain	Mild	High	Weak	Yes 2
D5	Rain	Cool	Normal	Weak	Yes 3
D6	Rain	Cool	Normal	Strong	No
D7	Overcast	Cool	Normal	Strong	Yes 4
D8	Sunny	Mild	High	Weak	No
D9	Sunny	Cool	Normal	Weak	Yes 5
D10	Rain	Mild	Normal	Weak	Yes 6
D11	Sunny	Mild	Normal	Strong	Yes 7
D12	Overcast	Mild	High	Strong	Yes 8
D13	Overcast	Hot	Normal	Weak	Yes 9
D14	Rain	Mild	High	Strong	No

（示例表格内的数据来自 https://wizardforcel.gitbooks.io/dm-algo-top10/content/naive-bayes.html）

可以将 Outlook， Temperature， Humidity， Wind，看做特征A1，A2, A3, A4 ;

那么分类标签Yes，可以看做B, No为B拔（互斥事件）。

由上图可以计算得到 P（Yes） = 9/14 , P(No) = 5 / 14,

特征之间完全独立，所以：

计算过程：

= （

） *

/ (

)

注： P（Sunny）* P(Hot) * P(High) * P(Weak) 表示纵向各特征值的占比，频率代替概率。

预测过程如下

①计算在 Sunny， Hot， High, Weak 特征条件下，分类为Yes的概率：

假设 P（Yes | Sunny， Hot， High, Weak）= Value1

② 计算在 Sunny， Hot， High, Weak 特征条件下，分类为No的概率：

P（No | Sunny， Hot， High, Weak） = Value2

注：因为类标签只有Yes和No，所以只需要计算2次。

③ 类分类判断

当且仅当：

Value1 > Value2时， Sunny， Hot， High, Weak 特征条件下，其分类为Yes

过程解释，假设有特征列X1，X2，X3,..., Xn；分类标签 Y1, Y2, Y3, ... , Yn：

计算:

P（Y1 | X1，X2, X3, ..., Xn）= Value1 ,

P（Y2 | X1，X2, X3, ..., Xn）= Value2 ,

P（Y1 | X1，X2, X3, ..., Xn）= Value3,

。

P（Yn | X1，X2, X3, ..., Xn）= ValueN，

选择：

max（Value1， Value2，..., ValueN）对应的 Yi作为当前数据的类标签。

之所以可以这样预测是因为训练集的数据给我们提供了先验概率和后验概率的值。

五. 代码实现

1. Sklearn里的Bayes使用

1 from sklearn.naive_bayes import MultinomialNB # 多项式

2 clf = MultinomialNB（）

3 clf.fit(train_set, train_label)

2. 上述代码解释

第1行，从sklearn的naive_bayes导入类MulitnomialNB （多项式贝叶斯）

第2行，创建多项式贝叶斯的对象

第3行，传入输入值（训练集特征）、标签属性（输入数据每行对应的标签值），开始训练模型。

3. Scipy-learn 中的函数及其参数

① 多项式朴素贝叶斯

class sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)

alpha=1.0 ， float, optional (default=1.0) ；平滑参数（拉普拉斯 / 利斯通）。

fit_prior=True， boolean, optional (default=True) ；是否学习先验概率， if False，使用统一的先验概率。

class_prior=None， array-like, size (n_classes,), optional (default=None)；先验概率，if 指定，不根据数据调整先验概率。

② 伯努利朴素贝叶斯

class sklearn.naive_bayes.BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None)

alpha=1.0 ， float, optional (default=1.0) ；平滑参数（拉普拉斯 / 利斯通）。

binarize=0.0， float or None, optional (default=0.0)；样本特征映射到boolean（二值化）上的阈值，if None ，假定输入为二值化特征。

fit_prior=True， boolean, optional (default=True) ；是否学习先验概率， if False，使用统一的先验概率。

class_prior=None， array-like, size (n_classes,), optional (default=None)；先验概率，if 指定，不根据数据调整先验概率。

③ 高斯朴素贝叶斯

class sklearn.naive_bayes.GaussianNB(priors=None)

priors=None， array-like, shape (n_classes,) ；先验概率，if 指定，不根据数据调整先验概率。

4. 3种朴素贝叶斯算法

A. Gaussian朴素贝叶斯，其特征符合正态分布（高斯分布）

B. Mutinomial朴素贝叶斯。

C. 伯努利朴素贝叶斯

ML————朴素贝叶斯原理和SKlearn相关库

猜你喜欢