算法原理 朴素贝叶斯法

朴素贝叶斯法

什么是朴素贝叶斯法？

是基于贝叶斯定理与特征条件独立假设的分类方法
对于给定的训练数据集 首先基于特征条件独立假设学习输入/输出的联合概率分布
然后基于此模型 对给定的输入x 利用贝叶斯定理求出后验概率最大的输出y
常用于:文档分类的算法

理论学习图谱

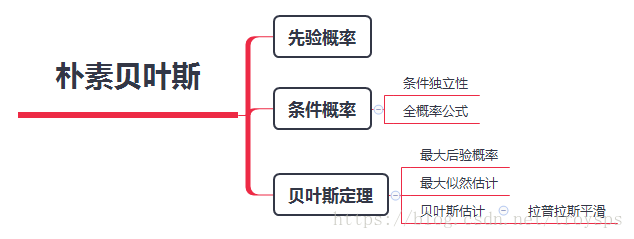
基本方法

1.首先将问题形式化 –用线性代数的思维分析数据集
数据集的一般表现形式 输入变量X与输入变量Y
数据集的输入变量X形式一般为以下情况 为$j\times n$维的矩阵

行\列	$x^{(1)}$	$x^{(2)}$	$x^{(3)}$	…	$x^{(n)}$
$x^{(1)}$	$x_1$	$x_1$	$x_1$	…	$x_1$
$x^{(2)}$	$x_2$	$x_2$	$x_2$	…	$x_2$
$x^{(3)}$	$x_3$	$x_3$	$x_3$	…	$x_3$
…	…	…	…	…	…
$x^{(j)}$	$x_j$	$x_j$	$x_j$	…	$x_j$

但是并不符合机器学习的实际需要 正确的输入变量X形式应该为$n\times j$维的矩阵 – 方便进行运算（如在线性回归中的 假设函数: $h(x) = W^T X$）
转置输入变量X

行\列	$x^{(1)}$	$x^{(2)}$	$x^{(3)}$	…	$x^{(j)}$
$x^{(1)}$	$x_1$	$x_2$	$x_3$	…	$x_j$
$x^{(2)}$	$x_1$	$x_2$	$x_3$	…	$x_j$
$x^{(3)}$	$x_1$	$x_2$	$x_3$	…	$x_j$
…	…	…	…	…	…
$x^{(n)}$	$x_1$	$x_2$	$x_3$	…	$x_j$

记输入变量$X \in R^n$为一个n维向量，输出变量$Y \in \left\{ c_1, c_2, c_3, ..., c_K \right\}$表示K个不同的类别
输入和输出服从联合概率分布$P(X, Y)$。我们的训练数据和测试数据都是服从这个联合概率分布，独立同分布的产生的。
这里只考虑使用训练数据的情况。如果我们有N个训练数据，训练集可以被记做$T = \left\{ (x_1,y_1), (x_2, y_2), ..., (x_N, y_N) \right\}。$

预测过程:在知道了输出变量$X$的条件下 求取得$Y$的每一个类别的概率 去其中类别概率最大作为其目标变量 – 分类

基于贝叶斯定理的推导过程

先验概率分布

$P(Y=c_k), k=1,2....k$

条件概率分布

$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},....X^{(n)}=x^{(n)}|Y=c_k),k=1,2,....,k$
条件概率定理
$假设事件A发生的概率为P(A)，如果获得了新的信息–确知另一个事件B已经发生 我们希望利用这一新的信息来重新计算事件A发生的可能性。 此时， 事件A发生的可能性叫做条件概率 记作P(A∣B),读作”事件B发生的条件下事件A发生的概率“ 条件概率： P(A∣B)=\frac {P(A∩B)}{P(B)} 或 P(B∣A)=\frac {P(A∩B)}{P(A)}$

扩展
相应事件 事件A发生的概率受到事件B发生与否的影响
独立事件 事件A发生的概率不受到事件B发生与否的影响
独立事件的乘法公式： P(A∩B)=P(A)P(B)
朴素贝叶斯法对条件概率分布做了条件独立性的假设
具体定理
$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},....X^{(n)}=x^{(n)}|Y=c_k)=\prod\limits_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k)$

后验概率分布

朴素贝叶斯分类时 对给定的输入 通过学习到的模型计算后验概率$P(Y=c_k|X=x)$ 将后验概率最大的类作为输入向量的类输出
计算定理为:
$P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{P(X=x)}=\frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_{k}P(X=x|Y=c_k)P(Y=c_k)}$

对于给定的输入向量$x$ 分子都是相同的
因此 预测函数可以写作
$y=f(x)=\arg\max \limits_{k} P(X=x|Y=c_k)P(Y=c_k)$
但是在实际情况中 $X$是一个高维向量 通常存在维度灾难的问题 刻画这个分布需要的参数也是指数级别的 **在朴素贝叶斯中 $X$的每一维都是相互独立的
**
因此引入条件概率公式
$P(X=x|Y=c_k)=\prod\limits_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k)$
那么最终的后验概率公式 变为
$\begin{align*} f(x)=\arg\max\limits_{k} P(X=x|Y=c_k)P(Y=c_k) = \arg\max\limits_{k} P(Y=c_k)\prod_{j=1}^{n} P(X^{(j)}=x^{(j)}|Y=c_k) \end{align*}$
预测问题转变为
先验概率 – k类发生的概率
条件概率 – 当k类方法时 n维特征中事件 $x^{(j)}$发生的概率
以上两者的乘积
通常认为$X$的取值是离散的

极大似然估计(maximum likelihood)

从观测数据中估计概率模型参数的方法
基本思想可以描述为，寻找一个参数使得给定的观测数据的概率最大
那么怎么寻找这样的一个参数?
首先 先说结果
极大似然估计中 概率近似等同于频率
$X和Y$是训练数据 可以使用离散概率分布中二项分布做比喻
推导二项概率分布的最大似然估计

假设观测数据服从$X\sim B(N,p)$
实际数据 $x=k$
似然函数为$L(p;k)=C_{n}^{k}p^k(1-p)^{n-k}$
求最大似然估计 对似然估计求导
$\frac{\partial}{\partial p}\ln L(p;k)=(\frac{k}{p}-\frac{N-k}{1-p})=0$
解得$p=\frac{k}{N}$

符合观点 概率近似等同于频率

证明了最大似然估计 接下来使用最大似然估计来估计朴素贝叶斯方法
$P(X^{(j)}=x^{(j)}|Y=c_k)=\frac{\sum_{i=1}^{N}I(x_i^{(j)}=x^{(j)},y_i=c_k)}{\sum_{i=1}^{N}I(y_i=c_k)}$

$P(Y=c_k)=\frac{\sum_{i=1}^{N}I(y_i=c_k)}{N}$
其中$I$是指标函数，表示满足内部的条件取值为1，不满足取值为0。
上面的式子对各个概率的估计实际上也就是统计其在训练数据中的频数。

存在问题 最大似然估计 在分母或者分子变为0时 处理数据会发生错误

贝叶斯估计 –解决极大似然估计的问题

使用拉普拉斯平滑
$P(X^{(j)}=x^{(j)}|Y=c_k)=\frac{\sum_{i=1}^{N}I(x_i^{(j)}=x^{(j)},y_i=c_k) + \lambda}{\sum_{i=1}^{N}I(y_i=c_k) + S_j\lambda}$
式中 $\lambda \ge 0$ 等价于在随机变量各个取值的频数上赋予一个正数 $\lambda$
当$\lambda=0$时 就是极大似然估计 $\lambda=1$时 称为拉普拉斯平滑
同样先验概率的贝叶斯估计是
$P(Y=c_k)=\frac{\sum_{i=1}^{N}I(y_i=c_k + \lambda)}{N + K\lambda}$

李航统计学习方法中 关于极大似然估计与贝叶斯估计两种方法估计的例子
极大似然估计


贝叶斯估计

参考文献
李航统计学习方法
贝叶斯统计观点下的拉普拉斯平滑
最大似然估计和最小二乘法怎么理解？