后附完整源代码:(含有求最大公倍数的函数,此代码测试的是面对不同组数据,各种算法的性能分析,如需输出最大公约数,只需加个输出就好!)
一、 题目分析
首先,题目要求我们求出俩个正整数的最大公约数和最小公倍数,并提供了6种不同的算法(递归与非递归算俩种)
1. 辗转相除法:此种方法核心如其名,辗转,大数放a中,小数放b中。大的除以小的,余数为零,则小数为最大公约数,不为零则,将余数与b比较大的放a,小的放b,如此往复!
2. 穷举法:看到这个穷举就知道它是最吃力不讨好的算法了。一个个穷举不仅浪费CPU,还浪费时间对吧,对两个正整数a,b如果能在区间[a,0]或[b,0]内能找到一个整数temp能同时被a和b所整除,则temp即为最大公约数。
3. 更相减损术:
第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。
则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。
其中所说的“等数”,就是最大公约数。求“等数”的办法是“更相减损”法。所以更相减损法也叫等值算法!
4. Stein算法:
通过数学的思想进行验证出:对于俩个俩个正整数数(x>y):
均为偶数gcd(x,y)=2gcd(x/2,y/2);
均为奇数gcd(x,y)=gcd((x+y)/2,(x-y)/2);
x奇y偶gcd(x,y)=gcd(x,y/2);
x偶y奇gcd(x,y) =gcd(x/2,y)或gcd(x,y)=gcd(y,x/2);
也就是说可以对俩奇俩偶和一奇一偶的情况进行化简,使其更容易计算。
又因为该算法采用位移运算所以减少了很多时间,所以也是很厉害的算法。
我们的主要目的是为了比较各个算法的性能优劣,通过程序的运行,输出不同算法计算20,40,80…200组甚至更大的数据的计算时间。
二、 算法构造
可爱的狗狗走错片场:

① 辗转相除法(非递归):
算法流程图:

② 辗转相除法(非递归):
算法盒图:

③ 辗转相除法(递归):

④ 辗转相除法(递归盒图):

⑤ 穷举法流程图:

⑥ 穷举法(盒图):

⑦ 更相减损术(流程图):

⑧ 更相减损术(盒图):

⑨ Stein算法(流程图):

⑩ Stein算法(递归盒图):

三、 算法实现
#include<iostream>
using namespace std;
#include<math.h>
#include<windows.h>
#include<time.h>
class Math
{
private:
int temp;
public:
int divistor(int,int); //NO.1,辗转相除法
int multiple(int,int);
int digui(int,int); //NO.2,辗转相除法递归
int multiple1(int,int);
int divistor3(int,int);//NO.3,穷举法
int multiple3(int,int);
int divistor4(int,int);//NO.4,更相减损术
int multiple4(int,int);
int gcd(int,int); //NO.5,stein算法递归算法
int multiple5(int,int);//求最大公倍数
int gcd1(int,int); //NO.6,stein算法非递归算法
int multiple6(int,int);//求最大公倍数
};
int Math::divistor(int x,int y)//x是大数,y是小数,非递归实现 NO.1
{
if(x<y)
{
temp=x;
x=y;
y=temp;
}
while(y!=0) //当y是0时,最大公约数就是x;
{
temp=x%y;
x=y; //这3句不能交换位置,否则temp值会出错
y=temp;
}
return x;
}
int Math::multiple(int x,int y) //求最大公倍数
{
temp=divistor(x,y);//
return ((x*y)/temp);
}
int Math::digui(int x,int y)//无需区别x,y的大小,递归方法
{
if(x%y==0)
return y;
else
return digui(y,x%y);
}
int Math::multiple1(int x,int y) //求最大公倍数
{
temp=digui(x,y);
return ((x*y)/temp);
}
int Math::divistor3(int x,int y)
{
temp=(x>y)?y:x;
while(temp>0)
{
if(x%temp==0&&y%temp==0)
break;
else temp--;
}
return temp;
}
int Math::multiple3(int x,int y)
{
int p,q;
p=x>y?x:y;//xiaozhi
q=x>y?y:x;//dazhi
temp=p;
while(1)
{
if(p%q==0)
break;
else
p+=temp;
}
return p;
}
int Math::divistor4(int x,int y)
{
int i=0;
int z=1;
while(x%2==0 && y%2==0) //判断m和n能被多少个2整除
{
x/=2;
y/=2;
i+=1;
}
if(x<y) //x是大数
{
temp=x;
x=y;
y=temp;
}
while(z)
{
z=x-y;
x=(y>z)?y:z;
y=(y<z)?y:z;
if(y==x)
break;
}
if(i==0)
return y;
else
return (int )pow(2,i)*y;
}
int Math::multiple4(int x,int y) //求最大公倍数
{
temp=divistor4(x,y);
return ((x*y)/temp);
}
int Math::gcd(int x,int y) //stein算法递归算法
{
if(x<y) //x是大数
{
temp=x;
x=y;
y=temp;
}
if(y==0) return x;
if((x&0x1)==0&&(y&0x1)==0) return 2*gcd(x>>1,y>>1); //俩数都是偶数
if((x&0x1)==0&&(y&0x1)!=0) return gcd(x>>1,y); //一偶一奇
if((x&0x1)!=0&&(y&0x1)==0) return gcd(x,y>>1); //一奇一偶
if((x&0x1)!=0&&(y&0x1)!=0) return gcd((x-y)>>1,y); //俩奇
}
int Math::multiple5(int x,int y) //求最大公倍数
{
temp=gcd(x,y);
return ((x*y)/temp);
}
int Math::gcd1(int a,int b) //stein算法非递归
{
int acc=0;
while((a&0x1)==0&&(b&0x1)==0)
{
++acc;
a>>=1;
b>>=1;
}
while((a&0x1)==0) a>>=1;
while((b&0x1)==0) b>>=1;
if(a<b) {int t=a; a=b; b=t;}
while((a=(a-b)>>1)!=0)
{
while((a&0x1)==0) a>>=1;
if (a<b) {int t=a; a=b; b=t;}
}
return b<<acc;
}
int Math::multiple6(int x,int y) //求最大公倍数
{
temp=gcd1(x,y);
return ((x*y)/temp);
}
int main()
{
int x,y,i,t; //t为数组的元素个数
char c[20]; //用于判断整数的正确性
Math m; //创建对象m
double z;
LARGE_INTEGER nFreq; //时间
LARGE_INTEGER nBeginTime;
LARGE_INTEGER nEndTime;
QueryPerformanceFrequency(&nFreq);
cout<<"请输入小于10000的测试组数(正整数:一组俩个数):"<<endl;
cin.getline(c,7); //7为函数读取的制定字符
if((c[0]-48)<=0||(c[0]-48)>9) {cout<<"输入的不是正整数,请重新输入!"; return 0;}
for(i=1;i<20;i++)
{
if(c[i]=='\0') break;
if((c[i]-48)<0||(c[0]-48)>9) {cout<<"输入的不是正整数,请重新输入!"; return 0;}
}
i=atoi(c);
if(i<0||i>10000) {cout<<"输入数超出范围,请重新输入!"; return 0;}
int a[20000];
t=2*i;
srand((unsigned)time(NULL)); //产生随机数种子,避免产生的随机数相同
for(i=0;i<t;i++) //初始化数组
{
a[i]=rand();
}
QueryPerformanceCounter(&nBeginTime);//开始计时
for(i=0;i<t;i++)
{
x=a[i];
y=a[i+1];
i+=1; //让x,y正好取得数组中的元素,如果没有i+=1会出错
m.divistor(x,y);
//m.multiple(x,y);
}
QueryPerformanceCounter(&nEndTime);//结束计时
z=(double)(nEndTime.QuadPart-nBeginTime.QuadPart)/(double)nFreq.QuadPart;//计算程序执行时间单位为s
cout<<"辗转相除法非递归所用时长:"<<z*1000<<"毫秒"<<endl;
QueryPerformanceCounter(&nBeginTime);//开始计时
for(i=0;i<t;i++)
{
x=a[i];
y=a[i+1];
i+=1; //让x,y正好取得数组中的元素,如果没有i+=1会出错
m.digui(x,y);
//m.multiple1(x,y);
}
QueryPerformanceCounter(&nEndTime);//结束计时
z=(double)(nEndTime.QuadPart-nBeginTime.QuadPart)/(double)nFreq.QuadPart;//计算程序执行时间单位为s
cout<<"辗转相除法递归所用时长:"<<z*1000<<"毫秒"<<endl;
QueryPerformanceCounter(&nBeginTime);//开始计时
for(i=0;i<t;i++)
{
x=a[i];
y=a[i+1];
i+=1; //让x,y正好取得数组中的元素,如果没有i+=1会出错
m.divistor3(x,y);
//m.multiple3(x,y);
}
QueryPerformanceCounter(&nEndTime);//结束计时
z=(double)(nEndTime.QuadPart-nBeginTime.QuadPart)/(double)nFreq.QuadPart;//计算程序执行时间单位为s
cout<<"穷举法所用时长:"<<z*1000<<"毫秒"<<endl;
QueryPerformanceCounter(&nBeginTime);//开始计时
for(i=0;i<t;i++)
{
x=a[i];
y=a[i+1];
i+=1; //让x,y正好取得数组中的元素,如果没有i+=1会出错
m.divistor4(x,y);
//m.multiple4(x,y);
}
QueryPerformanceCounter(&nEndTime);//结束计时
z=(double)(nEndTime.QuadPart-nBeginTime.QuadPart)/(double)nFreq.QuadPart;//计算程序执行时间单位为s
cout<<"更相减损术法所用时长:"<<z*1000<<"毫秒"<<endl;
QueryPerformanceCounter(&nBeginTime);//开始计时
for(i=0;i<t;i++)
{
x=a[i];
y=a[i+1];
i+=1; //让x,y正好取得数组中的元素,如果没有i+=1会出错
m.gcd(x,y);
//m.multiple5(x,y);
}
QueryPerformanceCounter(&nEndTime);//结束计时
z=(double)(nEndTime.QuadPart-nBeginTime.QuadPart)/(double)nFreq.QuadPart;//计算程序执行时间单位为s
cout<<"stein算法非递归所用时长:"<<z*1000<<"毫秒"<<endl;
QueryPerformanceCounter(&nBeginTime);//开始计时
for(i=0;i<t;i++)
{
x=a[i];
y=a[i+1];
i+=1; //让x,y正好取得数组中的元素,如果没有i+=1会出错
m.gcd1(x,y);
//m.multiple6(x,y);
}
QueryPerformanceCounter(&nEndTime);//结束计时
z=(double)(nEndTime.QuadPart-nBeginTime.QuadPart)/(double)nFreq.QuadPart;//计算程序执行时间单位为s
cout<<"stein算法递归所用时长:"<<z*1000<<"毫秒"<<endl;
return 0;
}
四、运行结果:
③结果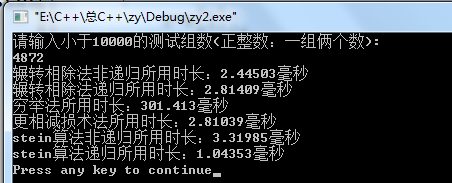
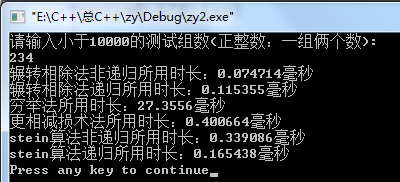
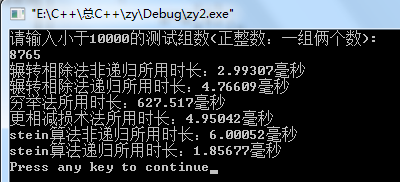
通过不同组数据的测试我们发现:
当数据小的时候:辗转相除法,更相减损术,stein算法,都比较用时少。
只有穷举法用时最长。(此时区别还不明显!)
但数据变大的时候:stein递归算法的好处就显现出来,次之的就是辗转相除法(非递归)了。
五、总结
这次的上机报告真的收获了许多,比较算法我也在上学期做过,比较不同排序的算法性能,当时用的是clock()函数,因为测试的数据比较庞大,有30000组数据,所以clock()函数已经足够显现出算法的区别。但是这次的程序,让我学到了一个新的测试时间的函数,它更精确,区别更明显!
高精度时控函数QueryPerformanceFrequency(),QueryPerformanceCounter()
原理:
QueryPerformanceCounter()这个函数返回高精确度性能计数器的值,它可以以微妙为单位计时.但是QueryPerformanceCounter()确切的精确计时的最小单位是与系统有关的,所以,必须要查询系统得到QueryPerformanceCounter()返回的嘀哒声的频率. QueryPerformanceFrequency()提供了这个频率值,返回每秒嘀哒声的个数. 计算确切的时间是从第一次调用QueryPerformanceCounter()开始的 假设得到的LARGE_INTEGER为nStartCounter,过一段时间后再次调用该函数结的, 设得到nStopCounter. 两者之差除以QueryPerformanceFrequency()的频率就是开始到结束之间的秒数.由于计时函数本身要耗费很少的时间,要减去一个很少的时间开销.但一般都把这个开销忽略。
还有对字符串有了更深一步的理解,cin,cin.getline(),cin.get()函数的区别!
cin.get()函数与cin.getline()函数区别:
cin.getline():在遇到回车符时,结束字符串输入并丢弃回车符。
cin.get():在遇到回车符时,则会保留回车符在输入队列。