偏微分方程的数值解(二): 一维状态空间的偏微分方程的 MATLAB 解法

3.1 工具箱命令介绍

MATLAB 提供了一个指令 pdepe，用以解以下的 PDE 方程式

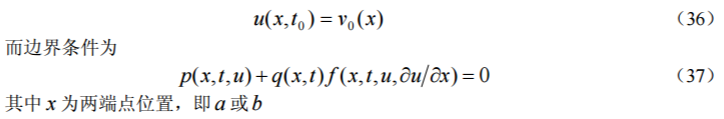
其中 x 为两端点位置，即a 或b

用以解含上述初始值及边界值条件的偏微分方程的 MATLAB 命令 pdepe 的用法如下：

 sol = pdepe(m, pdepe,icfun,bcfun, xmesh,tspan,options)

注：

1. MATLAB PDE 求解器 pdepe 的算法，主要是将原来的椭圆型和拋物线型偏微分方程转化为一组常微分方程。此转换的过程是基于使用者所指定的 mesh 点，以二阶空间离散化(spatial discretization)技术为之(Keel and Berzins,1990)，然后以 ode15s 的指令求解。采用 ode15s 的 ode 解法，主要是因为在离散化的过程中，椭圆型偏微分方程被转化为一组代数方程，而拋物线型的偏微分方程则被转化为一组联立的微分方程。因而，原偏微分方程被离散化后，变成一组同时伴有微分方程与代数方程的微分代数方程组，故以 ode15s 便可顺利求解。

2. x 的取点(mesh)位置对解的精确度影响很大，若 pdepe 求解器给出“…has difficulty finding consistent initial considition”的讯息时，使用者可进一步将 mesh 点取密一点，即增加 mesh 点数。另外，若状态u 在某些特定点上有较快速的变动时，亦需将此处的点取密集些，以增加精确度。值得注意的是 pdepe 并不会自动做 xmesh 的自动取点，使用者必须观察解的特性，自行作取点的操作。一般而言，所取的点数至少需大于 3 以上。

3. tspan 的选取主要是基于使用者对那些特定时间的状态有兴趣而选定。而间距(step size)的控制由程序自动完成。

4. 若要获得特定位置及时间下的解，可配合以 pdeval 命令。使用格式如下：

[ uout, duoutdx ] = pdeval(m, xmesh,ui, xout)

其中 m 代表问题的对称性。m =0 表示平板；m =1 表示圆柱体；m =2 表示球体。其意义同 pdepe 中的自变量m 。

ref. Keel,R.D. and M. Berzins,“A Method for the Spatial Discritization of Parabolic Equations in One Space Variable”，SIAM J. Sci. and Sat. Comput.,Vol.11,pp.1-32,1990.

以下将以数个例子，详细说明 pdepe 的用法。

3.2 求解一维偏微分方程

例 2 试解以下之偏微分方程式

解下面将叙述求解的步骤与过程。当完成以下各步骤后，可进一步将其汇总为一主程序 ex20_1.m，然后求解。

步骤 1 将欲求解的偏微分方程改写成如式的标准式。

步骤 2 编写偏微分方程的系数向量函数。

function [c,f,s]=ex20_1pdefun(x,t,u,dudx) 
c=pi^2;
f=dudx;
s=0;

步骤 3 编写起始值条件。

function u0=ex20_1ic(x)
u0=sin(pi*x);

步骤 4 编写边界条件。

在编写之前，先将边界条件改写成标准形式，如式（37），找出相对应的 p(⋅) 和 q(⋅) 函数，然后写出 MATLAB 的边界条件函数，例如，原边界条件可写成

因而，边界条件函数可编写成

function [pl,ql,pr,qr]=ex20_1bc(xl,ul,xr,ur,t)
pl=ul;
ql=0;
pr=pi*exp(-t);
qr=1;

步骤 5 取点。例如

x=linspace(0,1,20); %x 取 20 点
t=linspace(0,2,5); %时间取 5 点输出

步骤 6 利用 pdepe 求解。

m=0; %依步骤 1 之结果
sol=pdepe(m,@ex20_1pdefun,@ex20_1ic,@ex20_1bc,x,t);

步骤 7 显示结果。

u=sol(:,:,1);
surf(x,t,u)
title('pde 数值解')
xlabel('位置')
ylabel('时间' )
zlabel('u')

若要显示特定点上的解，可进一步指定 x 或 t 的位置，以便绘图。例如，欲了解时间为 2(终点)时，各位置下的解，可输入以下指令(利用 pdeval 指令)：

figure(2); %绘成图 2
M=length(t); %取终点时间的下标
xout=linspace(0,1,100); %输出点位置
[uout,dudx]=pdeval(m,x,u(M,:),xout);
plot(xout,uout); %绘图
title('时间为 2 时,各位置下的解')
xlabel('x')
ylabel('u')

综合以上各步骤，可写成一个程序求解例 2。其参考程序如下

function ex20_1
%************************************
%求解一维热传导偏微分方程的一个综合函数程序
%************************************
m=0;
x=linspace(0,1,20); %xmesh
t=linspace(0,2,20); %tspan
%************
%以 pde 求解
%************
sol=pdepe(m,@ex20_1pdefun,@ex20_1ic,@ex20_1bc,x,t);
u=sol(:,:,1); %取出答案
%************
%绘图输出
%************
figure(1)
surf(x,t,u)
title('pde 数值解')
xlabel('位置 x')
ylabel('时间 t' )
zlabel('数值解 u')
%*************
%与解析解做比较
%*************
figure(2)
surf(x,t,exp(-t)'*sin(pi*x));
title('解析解')
xlabel('位置 x')
ylabel('时间 t' )
zlabel('数值解 u')
%*****************
%t=tf=2 时各位置之解
%*****************
figure(3)
M=length(t); %取终点时间的下表
xout=linspace(0,1,100); %输出点位置
[uout,dudx]=pdeval(m,x,u(M,:),xout);
plot(xout,uout); %绘图
title('时间为 2 时,各位置下的解')
xlabel('x')
ylabel('u')
%******************
%pde 函数
%******************
function [c,f,s]=ex20_1pdefun(x,t,u,dudx)
c=pi^2;
f=dudx;
s=0;
%****************** 
%初始条件函数
%******************
function u0=ex20_1ic(x)
u0=sin(pi*x);
%******************
%边界条件函数
%******************
function [pl,ql,pr,qr]=ex20_1bc(xl,ul,xr,ur,t)
pl=ul;
ql=0;
pr=pi*exp(-t);
qr=1;

例 3 试解以下联立的偏微分方程系统

解步骤 1：改写偏微分方程为标准式

步骤 2：编写偏微分方程的系数向量函数

function [c,f,s]=ex20_2pdefun(x,t,u,dudx)
c=[1 1]';
f=[0.024 0.170]'.*dudx;
y=u(1)-u(2);
F=exp(5.73*y)-exp(-11.47*y);
s=[-F F]';

步骤 3：编写初始条件函数

function u0=ex20_2ic(x)
u0=[1 0]';

步骤 4：编写边界条件函数

function [pl,ql,pr,qr]=ex20_2bc(xl,ul,xr,ur,t)
pl=[0 ul(2)]';
ql=[1 0]';
pr=[ur(1)-1 0]';
qr=[0 1]';

步骤 5：取点。由于此问题的端点均受边界条件的限制，且时间t 很小时状态的变动很大(由多次求解后的经验得知)，故在两端点处的点可稍微密集些。同时对于t 小处亦可取密一些。例如，

x=[0 0.005 0.01 0.05 0.1 0.2 0.5 0.7 0.9 0.95 0.99 0.995 1];
t=[0 0.005 0.01 0.05 0.1 0.5 1 1.5 2];

以上几个主要步骤编写完成后，事实上就可直接完成主程序来求解。此问题的参考程序如下：

function ex20_2
%*************************************** 
%求解一维偏微分方程组的一个综合函数程序
%***************************************
m=0;
x=[0 0.005 0.01 0.05 0.1 0.2 0.5 0.7 0.9 0.95 0.99 0.995 1];
t=[0 0.005 0.01 0.05 0.1 0.5 1 1.5 2];
%*************************************
%利用 pdepe 求解
%*************************************
sol=pdepe(m,@ex20_2pdefun,@ex20_2ic,@ex20_2bc,x,t);
u1=sol(:,:,1); %第一个状态之数值解输出
u2=sol(:,:,2); %第二个状态之数值解输出
%*************************************
%绘图输出
%*************************************
figure(1)
surf(x,t,u1)
title('u1 之数值解')
xlabel('x')
ylabel('t')
%
figure(2)
surf(x,t,u2)
title('u2 之数值解')
xlabel('x')
ylabel('t')
%***************************************
%pde 函数
%***************************************
function [c,f,s]=ex20_2pdefun(x,t,u,dudx)
c=[1 1]';
f=[0.024 0.170]'.*dudx;
y=u(1)-u(2);
F=exp(5.73*y)-exp(-11.47*y);
s=[-F F]';
%****************************************
%初始条件函数
%****************************************
function u0=ex20_2ic(x)
u0=[1 0]';
%****************************************
%边界条件函数
%****************************************
function [pl,ql,pr,qr]=ex20_2bc(xl,ul,xr,ur,t)
pl=[0 ul(2)]';
ql=[1 0]';
pr=[ur(1)-1 0]';
qr=[0 1]';