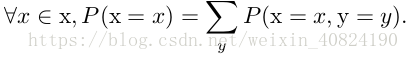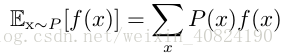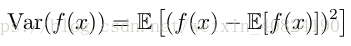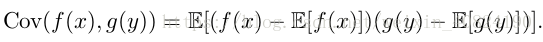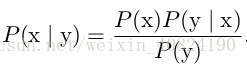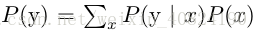深度学习（花书）读书笔记——第三章-概率与信息论

第三章 概率与信息论

        概率论是用于表示不确定性声明的数学框架。它不仅提供了量化不确定性的方法,也提供了用于导出新的不确定性 声明(statement)的公理。在人工智能领域,概率论主要有两种用途。首先,概率法则告诉我们 AI 系统如何推理,据此我们设计一些算法来计算或者估算由概率论导出的表达式。其次,我们可以用概率和统计从理论上分析我们提出的 AI 系统的行为。

3.2 随机变量

         随机变量(random variable)是可以随机地取不同值的变量。我们通常用无格式字体 (plain typeface) 中的小写字母来表示随机变量本身,而用手写体中的小写字母来表示随机变量能够取到的值。例如,x 1 和 x 2 都是随机变量 x 可能的取值。就其本身而言,一个随机变量只是对可能的状态的描述;它必须伴随着一个概率分布来指定每个状
态的可能性。

        随机变量可以是离散的或者连续的。离散随机变量拥有有限或者可数无限多的状态。注意这些状态不一定非要是整数;它们也可能只是一些被命名的状态而没有数值。连续随机变量伴随着实数值。

3.3 概率分布

        概率分布(probability distribution)用来描述随机变量或一簇随机变量在每一个可能取到的状态的可能性大小。我们描述概率分布的方式取决于随机变量是离散的还是连续的。

3.3.1 离散型变量和概率质量函数

        离散型变量的概率分布可以用 概率质量函数(probability mass function, PMF)来描述。

有时我们会先定义一个随机变量,然后用 ∼ 符号来说明它遵循的分布:x ∼ P (x)。
        概率质量函数可以同时作用于多个随机变量。这种多个变量的概率分布被称为 联合概率分布(joint probability distribution)。P (x = x, y = y) 表示 x = x 和y = y 同时发生的概率。我们也可以简写为 P (x, y)。

3.3.2 连续型变量和概率密度函数

        当我们研究的对象是连续型随机变量时,我们用 概率密度函数(probability density function, PDF)而不是概率质量函数来描述它的概率分布。

        为了给出一个连续型随机变量的 PDF 的例子,我们可以考虑实数区间上的均匀分布。我们可以使用函数 u(x; a, b),其中 a 和 b 是区间的端点且满足 b > a。符号“;’’ 表示 ‘‘以什么为参数’’;我们把 x 作为函数的自变量,a 和 b 作为定义函数的参数。为了确保区间外没有概率,我们对所有的 x ̸∈ [a, b],令 u(x; a, b) = 0。在 [a, b]内,有 u(x; a, b) =1/（b-a)。我们可以看出任何一点都非负。另外,它的积分为1。我们通常用 x ∼ U (a, b) 表示 x 在 [a, b] 上是均匀分布的。

3.4 边缘概率

        有时候,我们知道了一组变量的联合概率分布,但想要了解其中一个子集的概率分布。这种定义在子集上的概率分布被称为 边缘概率分布(marginal probability distribution)。

例如,假设有离散型随机变量 x 和 y,并且我们知道 P (x, y)。我们可以依据下面的 求和法则(sum rule)来计算 P (x):

        ‘边缘概率’ 的名称来源于手算边缘概率的计算过程。当 P (x, y) 的每个值被写在由每行表示不同的 x 值,每列表示不同的 y 值形成的网格中时,对网格中的每行求和是很自然的事情,然后将求和的结果 P (x) 写在每行右边的纸的边缘处。对于连续型变量,我们需要用积分替代求和:

3.5 条件概率

        在很多情况下,我们感兴趣的是某个事件,在给定其他事件发生时出现的概率。这种概率叫做条件概率。我们将给定 x = x,y = y 发生的条件概率记为P (y = y | x = x)。这个条件概率可以通过下面的公式计算: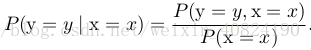

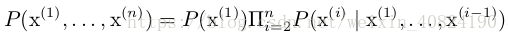
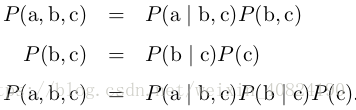
3.6 条件概率的链式法则

任何多维随机变量的联合概率分布,都可以分解成只有一个变量的条件概率相乘的形式：

这个规则被称为概率的 链式法则(chain rule)或者 乘法法则(product rule)。它可以直接从式 (3.5) 条件概率的定义中得到。例如,使用两次定义可以得到

3.7 独立性和条件独立性

        两个随机变量 x 和 y,如果它们的概率分布可以表示成两个因子的乘积形式,并且一个因子只包含 x 另一个因子只包含 y,我们就称这两个随机变量是 相互独立的(independent):

        我们可以采用一种简化形式来表示独立性和条件独立性:x⊥y 表示 x 和 y 相互独立,x⊥y | z 表示 x 和 y 在给定 z 时条件独立。

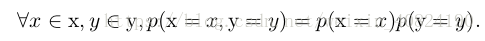
3.8 期望、方差和协方差

        函 数 f (x) 关 于 某 分 布 P (x) 的 期 望(expectation) 或 者 期 望 值(expected value)是指,当 x 由 P 产生,f 作用于 x 时,f (x) 的平均值。对于离散型随机变量,这可以通过求和得到:

对于连续型随机变量可以通过求积分得到:

期望是线性的,例如:其中 α 和 β 不依赖于 x。

方差(variance)衡量的是当我们对 x 依据它的概率分布进行采样时,随机变量 x 的函数值会呈现多大的差异

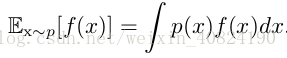
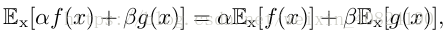
当方差很小时,f (x) 的值形成的簇比较接近它们的期望值。方差的平方根被称为标准差(standard deviation)。

协方差(covariance)在某种意义上给出了两个变量线性相关性的强度以及这些变量的尺度:

        协方差的绝对值如果很大则意味着变量值变化很大并且它们同时距离各自的均值很远。如果协方差是正的,那么两个变量都倾向于同时取得相对较大的值。如果协方差是负的,那么其中一个变量倾向于取得相对较大的值的同时,另一个变量倾向于取得相对较小的值,反之亦然。其他的衡量指标如 相关系数(correlation)将每个变量的贡献归一化,为了只衡量变量的相关性而不受各个变量尺度大小的影响。

        两个变量如果相互独立那么它们的协方差为零,如果两个变量的协方差不为零那么它们一定是相关的。然而,独立性又是和协方差完全不同的性质。两个变量相互依赖但具有零协方差是可能的。

3.9 常用概率分布

3.9.1 Bernoulli 分布

Bernoulli 分布 (Bernoulli distribution)是单个二值随机变量的分布。它由单个参数 φ ∈ [0, 1] 控制,φ 给出了随机变量等于 1 的概率。它具有如下的一些性质: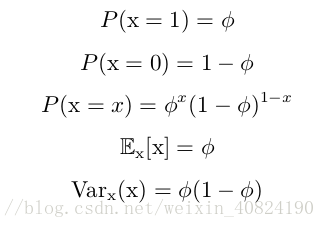

x	0	1
P	1-φ	φ

3.9.1 Multinoulli 分布

3.9.3 高斯分布

实数上最常用的分布就是 正态分布(normal distribution),也称为 高斯分布(Gaussian distribution):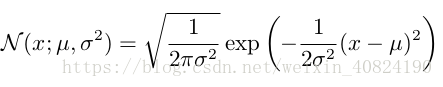

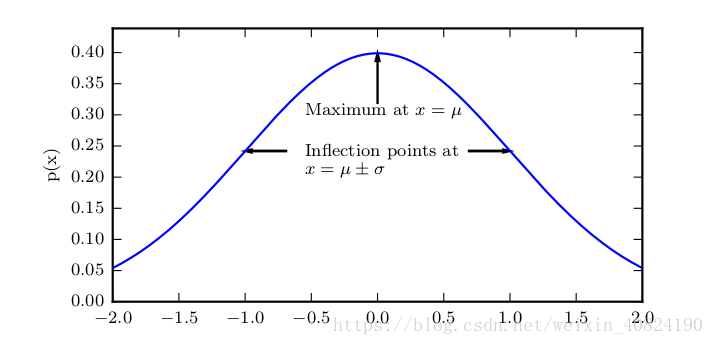
正态分布由两个参数控制,μ ∈ R 和 σ ∈ (0, ∞)。参数 μ 给出了中心峰值的坐标,这也是分布的均值:E[x]=μ。分布的标准差用 σ 表示,方差用 σ 2 表示。

        正态分布 N (x; μ, σ 2 ) 呈现经典的 ‘钟形曲线’ 的形状,其中中心峰的 x 坐标由 μ 给出,峰的宽度受 σ 控制。在这个示例中,我们展示的是 标准正态分布(standard normaldistribution),其中 μ = 0, σ = 1。

        采用正态分布在很多应用中都是一个明智的选择。当我们由于缺乏关于某个实数上分布的先验知识而不知道该选择怎样的形式时,正态分布是默认的比较好的选择,其中有两个原因。

第一,我们想要建模的很多分布的真实情况是比较接近正态分布的。 中心极限定理(central limit theorem)说明很多独立随机变量的和近似服从正态分布。这意味着在实际中,很多复杂系统都可以被成功地建模成正态分布的噪声,即使系统可以被分解成一些更结构化的部分。

第二,在具有相同方差的所有可能的概率分布中,正态分布在实数上具有最大的不确定性。因此,我们可以认为正态分布是对模型加入的先验知识量最少的分布。

3.10 常用函数的有用性质

某些函数在处理概率分布时经常会出现,尤其是深度学习的模型中用到的概率分布。
其中一个函数是 logistic sigmoid 函数:

另外一个经常遇到的函数是 softplus 函数：

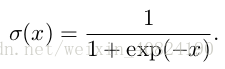
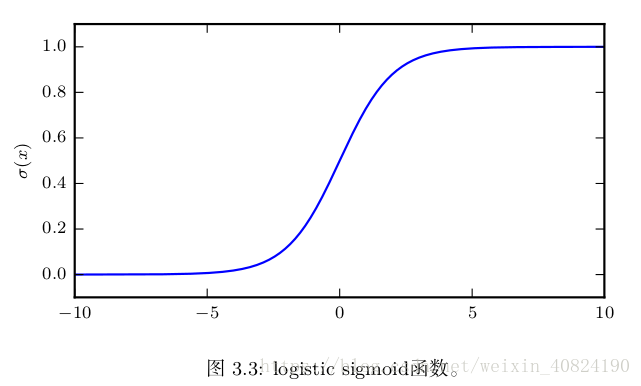
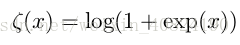
3.11 贝叶斯规则

我们经常会需要在已知 P (y | x) 时计算 P (x | y)。幸运的是,如果还知道 P (x),我们可以用贝叶斯规则(Bayes’ rule)来实现这一目的:

注意到 P (y) 出现在上面的公式中,它通常使用
所以我们并不需要事先知道 P (y) 的信息。