读书笔记 机器学习(周志华)第三章 线性模型
3.1 基本形式
线性模型(linear model)试图通过属性的线性组合来进行预测,即
,
一般用向量形式写成
,
其中w是
的向量,w和b学得之后,model就确定了。
3.2 线性回归
“线性回归”(linear regression)
“欧氏距离”(Euclidean distance)
“最小二乘法”(least square method)
“参数估计”:求解w和b使
最小化的过程,称为线性回归模型的最小二乘“参数估计”。
对w和b进行求导,可得到w和b的最优解。
“多元线性回归”(multivariate linear regression)



“对数线性回归”(loglog-linear regression):
,试图让
逼近y。
3.3 对数几率回归
线性回归模型产生的预测值 是实值,需要将实值转换为0/1值。
“单位跃阶函数”
“对数几率函数”(logistic function):
,是一种sigmoid函数。
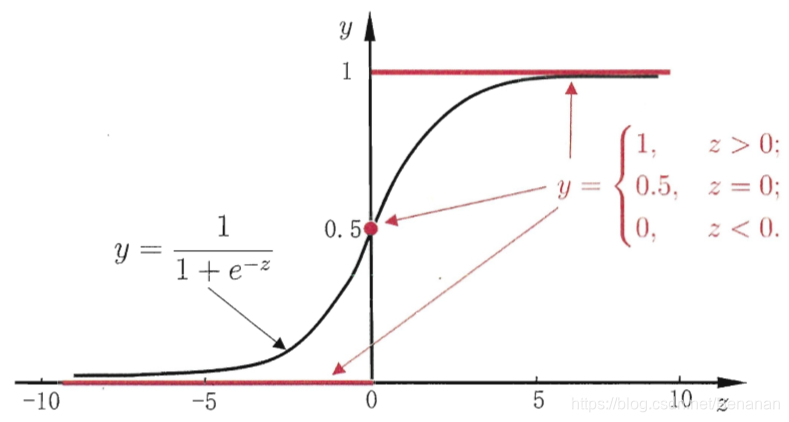
将z实值函数代入logistic function,得到
同理,可变化为
若y视为样本x正例的可能性,则1-y是其反例的可能性,两者比值
称为“几率”,反映x为正例的相对可能性。取对数则得到“对数几率”(log odds)。
以上对应模型为“对数几率回归”(logistic regression)。
3.4 线性判别分析
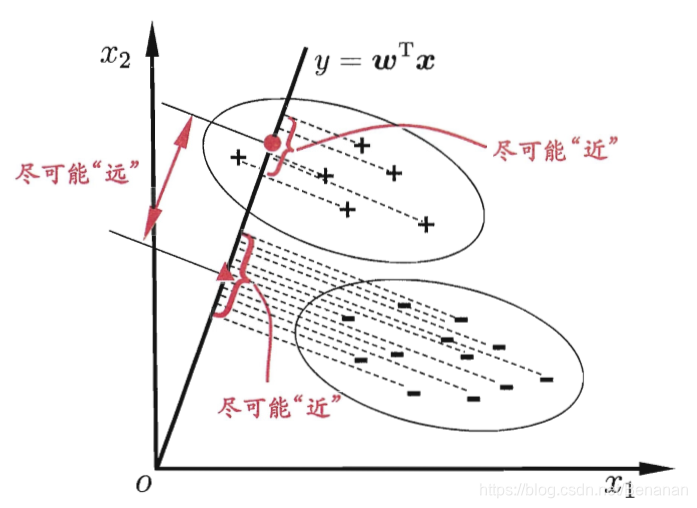
“线性判别分析”(Linear Discriminant Analysis,LDA):将所有样本对某一直线进行投影,使同类样本投影点距离尽量靠近,不同类点距离尽量远离。新样本同样做投影处理,通过投影距离判断样本类别。
3.5 多分类学习
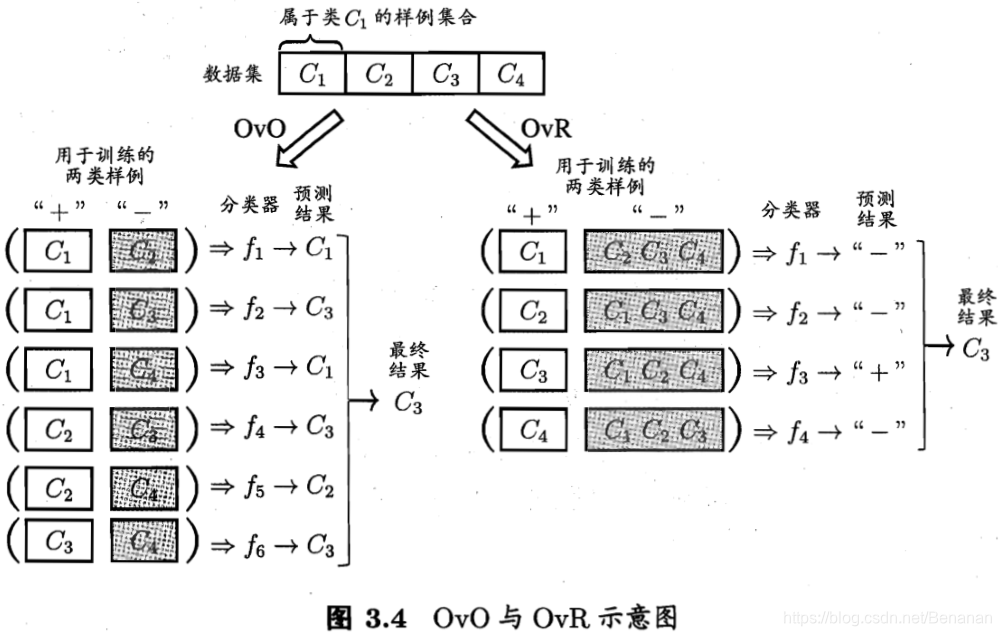
拆解法:将多分类任务拆为若干个二分类任务求解。

OvO:两两配对,产生N(N-1)/2个分类任务,将得到N(N-1)/2个结果,最终结果通过投票产生:把预测得最多的类别作为最终结果。
OvR:每次将一个类别作为正例,其他剩余作为反例,得到N个分类器。若仅有一个分类器预测为正类,则对应的标记作为最终分类结果。若有多个为正类,则考虑个分类器的预测置信度,选择置信度最大的类别作为分类结果。
3.6 类别不平衡问题
“类别不平衡”:指分类任务中不同类别的训练样例数目差别很大。