一切为了数据挖掘的准备
3.k近邻法
3.1 k近邻算法
- k邻近法可以解决分类和回归问题。本章只涉及到分类问题
- k邻近法三要素:k值的选择,距离度量、分类决策规则
- 算法(线性扫描):
- 输入:训练数据集T,输出:实例x所属的类y
- 根据给定的距离度量,在T中找出与待预测值x最邻近的k个点,涵盖这k个点的x的邻域记作
- 在 邻域中根据分类决策规则决定x的类别y: ,I为指示函数,当 时I为1,否则I为0.
- 最近邻算法:k=1
3.2 模型的要素
距离度量
设特征空间X是n维实数向量空间
,
,设有实例
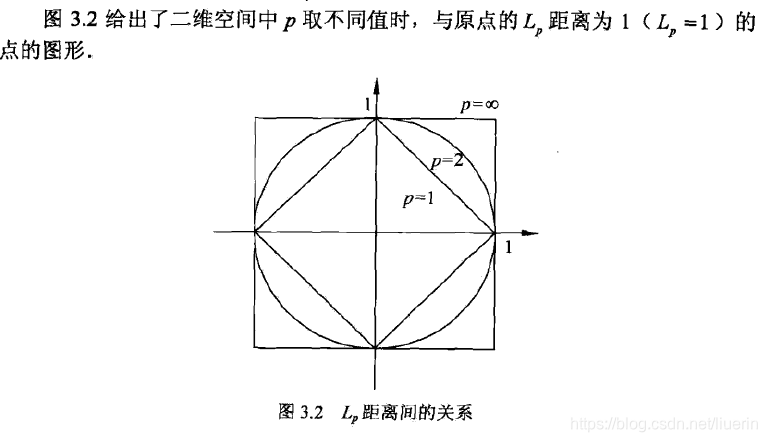
,距离
- p=2时为欧式距离
- p=1时为曼哈顿距离
-
时,是各个坐标距离的最大值
在计算距离时,可以将数据归一化,使不同的特征具有相同的权重,将特征值转化到0-1的区间。即各个特征的数据
k值的选择
- 如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预测,预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。所以k值的减少就意味着整体模型变得复杂,容易发生过拟合
- 如果选择较大k值,就相当于用较大的邻域中的训练实例进行预测,可能与输入实例点较远或不相似的训练实例也会对预测其作用,使预测发生错误。
分类决策规则
样本误分类率为:
假设最近邻的k个训练实例点构成集合
,如果涵盖此区域的类别是
,要是误分类率最小,即经验风险最小,就要使
最大,所以多数表决规则等价于经验风险最小化
3.3kd树
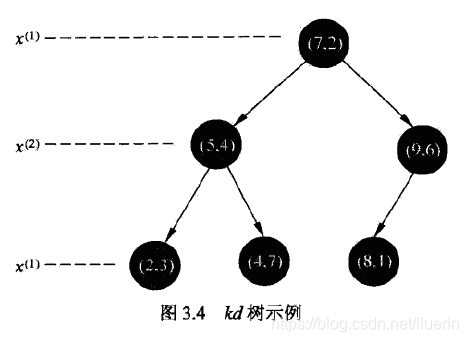
kd树是二叉树,表示对k维空间的切分。通常在选定的维度上取训练实例数据的中位数做切分点,这样得到的kd树是平衡的。
构造kd树的算法
- 构造根节点。在训练集T的所有实例中,选择 坐标的中位数为切分点,构成根结点。将数据集中剩余数据切分为左右两个区域。左区域对应坐标小于根结点 ,右区域 大于此值.
- 分别对左区域和右区域顺序选择下一个 轴选取中位数作切分。选择的切分点构成父节点的子节点。
- 轴可以循环选取进行划分,直至子区域没有实例存在时停止,从而形成kd树的区域划分。
搜索kd树的算法
- 从根结点出发,如果目标点当前维的坐标小于切分点坐标,移动到子节点;反之移动到右节点。直至寻找到包含目标点的叶节点。
- 将此叶节点作为”当前最近点“
- 递归回退
- 如果回退点的距离更近,将此回退点作为”当前最近点“
- 检查回退点的兄弟节点对应的区域是否和以目标点为球心,以当前最近距离为半径的区域相交;如果有,移动到兄弟节点进行搜索;如果没有,向上回退。
- 当回退到根结点时,搜索结束。
kd树适用于训练数据远大于空间维数时的k紧邻搜索。
3.4我的实现,不一定简便
import numpy as np
from pandas import DataFrame
class knn:
def __init__(self,x,y):
"""
训练集x,y
"""
self.x = np.array(x)
self.y = np.array(y)
def predict(self,x,k):
"""
待预测x,k邻近参数k
"""
x1 = np.array(x)
#计算欧式距离
dis = np.sqrt(np.sum((self.x-x1)*(self.x-x1),axis=1))
data = DataFrame([dis,self.y]).T
data.columns = ['dist','yvalue']
#根据距离排序,选择前k个
kdata = data.sort_values('dist')[:self.k]
#选择y值最多的类别
re = kdata.groupby('yvalue').count().sort_values(by='dist',ascending=False)[:1]
return re.index[0]
x=[[5,4],[9,6],[4,7],[2,3],[8,1],[7,2]]
y=[1,1,1,-1,-1,-1]
k = knn(1,x,y)
x0=[5,3]
k.predict(x0)
用sklearn
from sklearn.neighbors import KNeighborsClassifier
X=[[5,4],[9,6],[4,7],[2,3],[8,1],[7,2]]
y=[1,1,1,-1,-1,-1]
neigh = KNeighborsClassifier(n_neighbors=1)
neigh.fit(X,y)
print(neigh.predict([[5,3]]))