散记知识点

——“低质量的数据将导致低质量的挖掘结果。”

数据清理可以用来清除数据中的噪声，纠正不一致。数据集成将数据由多个数据源合并成一个一致的数据储存，如数据仓库。数据归约可以通过如聚集、删除冗余特征或聚类来降低数据的规模。数据变换（如，规范化）可以用来把数据压缩到较小的区间。

1. 数据预处理：概述

1.1 数据质量
数据质量涉及到许多因素，包括准确度、完整性、一致性、时效性、可信性和可解释性。

1.2 数据预处理的主要任务
数据预处理的主要步骤，即

数据清理：填充缺失值、光滑噪声并识别离群点、纠正数据中的不一致。
数据集成：合并来自多个数据储存的数据，减少结果数据集的冗余和不一致。
数据归约：用较小的数据集替换原数据集，保持原始数据的完整性。
数据变换：变换数据使得其适合于挖掘的形式。

2. 数据清理

2.1 缺失值

对于处理数据中的缺失值有以下几个方法：
(1) 忽略元组：适用于分类的挖掘任务缺少类标号时，当元组有多个属性缺少值，而且每个属性缺失值的百分比变化很小。可以采用忽略元组的方法。注意该元组剩余的属性值也不能被使用。
(2) 人工填写缺失值：方法费时，且不适用于大规模数据集。
(3) 使用一个全局常量填充缺失值：方法简单，但不可靠。
(4) 使用属性的中心度量(均值或中位数)填充缺失值：对于正常对称的数据分布，使用均值，对于倾斜数据则使用中位数。
(5) 使用与给定元组同一类的所有样本的属性均值或中位数
(6) 使用最可能的值填充缺失值：可以采用回归，贝叶斯法以及决策树等推理出缺失值。该方法最为常用，原因在于它使用已有数据的大部分信息来预测缺失值。

2.2 噪声数据

噪声定义：被测量的变量的随机误差或方差。

去除噪声，光滑数据方法：
(1) 分箱：通过考察数据的“近邻”(即周围的值)来光滑有序数据的值。这些有序的值被分布到一些桶或箱中，进行局部光滑。可以采用箱均值光滑、箱中位数光滑以及箱边界光滑。
(2) 回归：用一个函数拟合来光滑数据。线性回归，找出拟合两个属性的最佳直线，使得一个属性可以用来预测另一个。多元线性回归涉及的属性多于两个，数据拟合到一个多维平面上。
(3) 离群点分析：通过聚类来检测离群点，聚类将类似的值组织成群或“簇”，那些落在簇集合之外的值被视为离群点。

3. 数据集成

3.1 冗余和相关分析
如果一个属性能由另一个或另一组属性“导出”，则这个属性可能是冗余的。有些冗余可以通过相关分析检测到，给定两个属性可以根据可用的数据，度量一个属性能在多大程度上蕴含另一个。

(1)标称属性的 $\chi ^2$ (卡方)相关检验

假设属性A有c个不同值 $a_{1},a_{2},...,a_{c}$ ，属性B有r个不同值 $b_{1},b_{2},...,b_{r}$ 。A和B的元素构成一个矩阵表 $(c \times r)$ ，令 $(A_{i}, B_{i})$ 表示属性A取值 $a_{i}$ ，属性B取值 $b_{j}$ 的联合事件，即 $(A=a_{i}, B=b_{j})$ 。则 $\chi ^ 2$ 值(Pearson $\chi ^2$ 统计量)可以用下式计算：

χ^{2} = \sum_{i = 1}^{c} \sum_{j = 1}^{r} \frac{(o_{i j} - e_{i j})^{2}}{e_{i j}}

$\chi ^ 2=\sum_{i=1}^c \sum_{j=1}^r \frac{(o_{ij}-e_{ij})^2}{e_{ij}}$
其中，

o_{i j}

$o_{ij}$ 是联合事件

(A_{i}, B_{j})

$(A_{i}, B_{j})$ 的观测频度(即频数)，而

e_{i j}

$e_{ij}$ 是

(A_{i}, B_{j})

$(A_{i}, B_{j})$ 的期望频度，可以用下式计算：

e_{i j} = \frac{c o u n t (A = a_{i}) \times c o u n t (B = b_{j})}{n}

$e_{ij}=\frac{count(A=a_{i}) \times count(B=b_{j})}{n}$
其中。n是数据元组的个数，

c o u n t (A = a_{i})

$count(A=a_{i})$ 是A上具有值

a_{i}

$a_{i}$ 的元组个数，而

c o u n t (B = b_{j})

$count(B=b_{j})$ 是B上具有值

b_{j}

$b_{j}$ 的元组个数。
卡方统计检验假设A和B独立的。检验基于显著性水平，具有自由度

(r - 1) \times (c - 1)

$(r-1) \times (c-1)$ ，如果可以拒绝该假设，则可以说A和B相互独立的假设不正确，即A和B是统计相关的。
下图为一实例：
这里写图片描述

(2) 数值数据的相关系数
对于数值属性的数据，可以直接计算相关系数来度量两个属性之间的相关性，计算A和B的相关系数(Pearson积矩系数)如下：

r_{A, B} = \frac{\sum_{i = 1}^{n} (a_{i} - \bar{A}) (b_{i} - \bar{B})}{n σ_{A} σ_{B}} = \frac{\sum_{i = 1}^{n} (a_{i} b_{j}) - n \bar{A} \bar{B}}{n σ_{A} σ_{B}}

$r_{A,B}=\frac{\sum_{i=1}^n (a_{i}-\bar{A})(b_{i}-\bar{B})}{n\sigma_{A} \sigma_{B}}=\frac{\sum_{i=1}^n (a_{i}b_{j})-n\bar{A} \bar{B}}{n\sigma_{A} \sigma_{B}}$
其中，n是元组的个数，

a_{i}

$a_{i}$ 和

b_{i}

$b_{i}$ 分别是元组

i

$i$ 在A和B上的值；

\bar{A}

$\bar{A}$ 和

\bar{B}

$\bar{B}$ 分别是A和B的均值；

σ_{A}

$\sigma_{A}$ 和

σ_{B}

$\sigma_{B}$ 分别是A和B的标准差。

\sum (a_{i} b_{i})

$\sum(a_{i}b_{i})$ A和B的叉积和(内积和)。
相关系数(

- 1 ⩽ r_{A, B} ⩽ 1

$-1 \leqslant r_{A,B} \leqslant 1$ )，如果

r_{A, B}

$r_{A,B}$ 大于0，则A和B是正相关的。该值越大，相关性越强。因此较大的相关系数表明A或B可以作为冗余而被删除。

r_{A, B} = 0

$r_{A,B}=0$ 表示A和B是相互独立的，不存在相关性。

r_{A, B}

$r_{A,B}$ 小于表示A和B是负相关的。注意，相关性并不蕴涵因果关系，如果A和B是相关的，并不代表A导致B或B导致A。

(3) 数值数据的协方差
考虑两个数值属性A、B和n次观测集合 $\{ (a_{1}, b_{1}), ..., (a_{n}, b_{n})\}$ 则A和B的协方差(covariance)定义为：

C o v (A, B) = E ((A - \bar{A}) (B - \bar{B})) = E (A \cdot B) - \bar{A} \bar{B} = \frac{\sum_{i = 1}^{n} (a_{i} - \bar{A}) (b_{i} - \bar{B})}{n}

$Cov(A,B)=E((A- \bar{A})(B-\bar{B}))=E(A \cdot B)-\bar{A}\bar{B}=\frac{\sum_{i=1}^n (a_{i}-\bar{A})(b_{i}-\bar{B})}{n}$
它与相关系数的关系表示为：

r_{A, B} = \frac{C o v (A, B)}{σ_{A} σ_{B}}

$r_{A,B}=\frac{Cov(A,B)}{\sigma_{A}\sigma_B}$
如果A和B是独立的，则

E (A \cdot B) = E (A) \cdot E (B)

$E(A \cdot B)=E(A) \cdot E(B)$ ，此时协方差为0。反推不一定成立，即协方差为0不能说明A和B独立，除非A和B都服从正态分布。

4. 数据归约

数据归约策略包括维归约、数量归约和数据压缩：

维归约：减少属性个数，包括数据降维和特征子集选择等。降维方法主要有小波变化和主成分分析，把原数据变换或投影到较小的空间。特征子集选择将不相关、弱相关或冗余的属性剔除，最后构成最优特征子集。
数量归约：用较小的数据表示形式来替换原数据，可以是参数的或者非参数的，对于参数方法，使用模型估计数据，只需储存模型参数，如回归和对数-线性模型。非参数方法有直方图、聚类、抽样和数据立方体聚集。
数据压缩：使用变换，得到原数据的归约或压缩表示，分为有损压缩（原数据能够从压缩后的数据重构）和无损压缩（能近似重构原数据）。

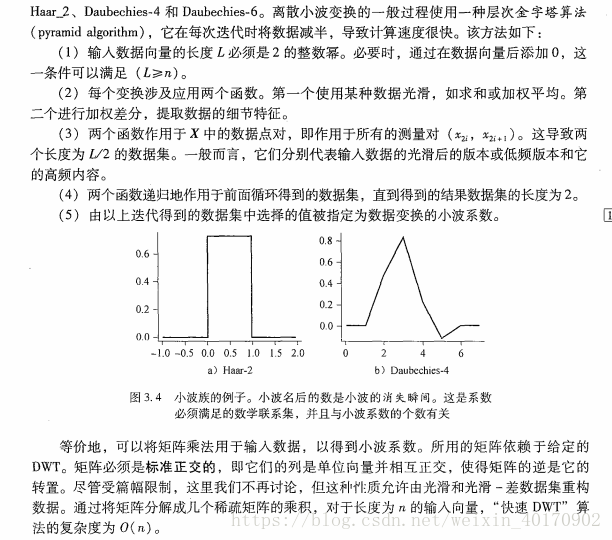
4.1 小波变换(DWT)
对向量 $\mathbf{X}$ 进行小波变换，会生成不同数值的小波系数构成向量 $\mathbf{X}^{'}$ ，原向量和变换后的向量具有相同的长度。小波变换后的数据可以截短，仅存放一小部分最强的小波系数，就能保留近似的压缩数据。例如，保留大于某个阈值的小波系数，其他系数置为0，则结果数据会变得很稀疏，在小波空间进行计算将会非常快，同时也能在一定程度上消除噪声，而不会光滑掉数据的主要特征，给定一组小波系数，使用逆小波变换，可以构造原数据的近似。小波变换的步骤如下图：这里写图片描述

4.2 主成分分析

主成分分析(principal components analysis PCA) 法，又称Karhunen-Loeve(K-L方法)法，搜索 $k$ 个最能代表数据的 $n$ 维正交向量，其中 $k \leqslant n$ 。这样，原数据就能投影到一个小得多的空间上，达到降维的效果。基本过程如下：

对数据规范化，一般将每个属性值归一化落入[0, 1]区间内。
PCA计算k个标准正交向量，作为规范化输入数据的基，这些单位向量相互正交，是为主成分。输入数据是主成分的线性组合。
对主成分按”主要性”一般是对应特征值大小降序排列，主成分本质上充当数据的新坐标系，提供关于方差的信息。即对坐标轴进行排序，使得第一个坐标轴显示数据的最大方差，第二个显示数据的次大方差。
去除较弱的成分(即方差较小的那些)来归约数据，使用最强的主成分能够重构原数据达到很好的近似。与小波变换相比，PCA能够更好地处理稀疏数据，而小波变换更适合高维数据。

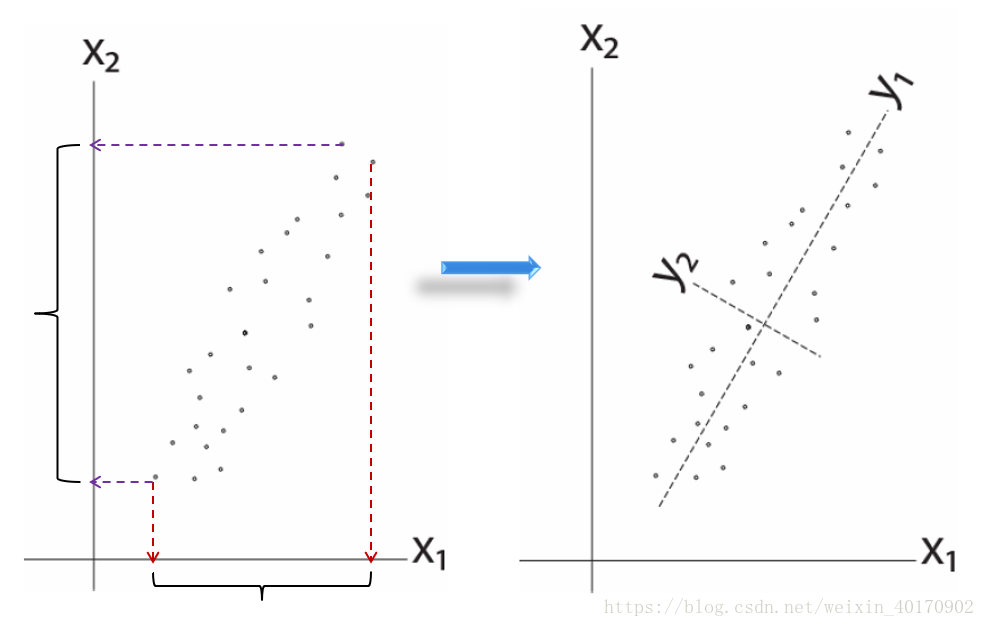
(1)二维空间的PCA主成分分析法推导：

这里写图片描述

原始数据在 $X1-X2$ 的坐标空间，接着为了方便计算自协方差矩阵进行（归一化？）规范中心化(即将所有点的均值中心放在原点)：
这里写图片描述
设数据点 $X$ 与自身的协方差为 $S(X)$ 则: $S(X)=\frac{1}{n-1}XX^T$ ，对原数据点进行一个坐标变换，去除每个数据点之间的相关性。则变换后的坐标轴即为Y1和Y2，代表两个主成分。设坐标变换为： $Y=PX$ 则，变化后的数据点的协方差矩阵为:

S (Y) = \frac{1}{n - 1} Y Y^{T} = \frac{1}{n - 1} (P X) (P X)^{T} = \frac{1}{n - 1} P X X^{T} P^{T}

$S(Y)=\frac{1}{n-1}YY^T=\frac{1}{n-1}(PX)(PX)^T=\frac{1}{n-1}PXX^TP^T$
设

X X^{T} = Q D Q^{T}

$XX^T=QDQ^T$ ，这一步是进行 奇异值分解，则：

(n - 1) S (Y) = P Q D Q^{T} P^{T} = (P Q) D (P Q)^{T}

$(n-1)S(Y)=PQDQ^TP^T=(PQ)D(PQ)^T$
为了保证

(n - 1) S (Y)

$(n-1)S(Y)$ 为对角阵则令

P Q = I

$PQ=I$ ，由于Q为正交阵，则得

P = Q^{- 1} = Q^{T}

$P=Q^{-1}=Q^T$ ，由此我们得到的

X \to Y

$X \to Y$ 的变换矩阵

P

$P$ ，该矩阵正是

X X^{T}

$XX^T$ 的特征矩阵的转置。
这里 为什么要保证矩阵 $(n-1)S(Y)$ 为对角阵呢？原因在于协方差矩阵

S (Y)

$S(Y)$ 。我们假设有两个属性A和B相关性未知，则二者的协方差矩阵为S(C)：

S (C) = [\begin{matrix} C o v (A, A) & C o v (A, B) \\ C o v (B, A) & C o v (B, B) \end{matrix}]

$S(C)=\left[\begin{matrix}Cov(A,A)&Cov(A,B)\\ Cov(B,A)&Cov(B,B)\end{matrix}\right]$
若保证属性A和B不相关（数据中不存在冗余）则

C o v (A, B) = C o v (B, A) = 0

$Cov(A,B)=Cov(B,A)=0$ ，也即互协方差矩阵为对角阵。

对于坐标系，原坐标系是以原来的两个属性 $X_{1}$ 和 $X_{2}$ 为横纵坐标轴，而得到的新的坐标轴 $Y_{1}$ 和 $Y_{2}$ 即为映射的特征空间“属性”。其中 $Y_{1}$ 和 $Y_{2}$ 的方向向量分别是原坐标系下的 $S(X)=\frac{1}{n-1}XX^T$ 的特征向量(对应的特征值 $\lambda_{1} > \lambda_{2}$ )。

最后一步也就是降维，一般我们取较大的特征值对应的特征向量为主向量，忽略较小特征值对应的特征向量(也就是所谓的最大方差准则？)，然后让主向量去加权对应相乘原始的两个属性数据结果得到一组数据(即原始的两个属性映射到了一个主“特征属性”上去了)，从而达到降维的目的。

至于最后一步怎么乘的，假设取前 $k$ 个特征值对应的 $n$ 维特征向量排成一个矩阵，则矩阵的大小为 $k \times n$ ，假设原始 $n$ 个属性数据每个属性有 $m$ 个值，则可以组成数据矩阵大小为 $n \times m$ ，前后两个矩阵相乘得到大小为 $k \times m$ 的 $k$ 个属性每个属性 $m$ 个值的新数据矩阵，从而达到降维的目的。

总结：所谓主成分分析法也就是将原始的 $n$ 个属性，映射到一个特征空间上，得到 $n$ 个彼此不相关的特征属性，然后取前 $k$ 个较大的特征值对应的特征向量为主成分方向向量，最后用 $k$ 个向量与原始 $n$ 个数据属性相乘得到 $k$ 组新的属性数据，使得数据由 $n$ 维降至 $k$ 维。

(2) 另一个角度理解PCA

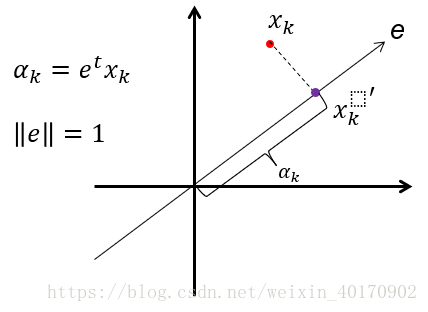
假设二维空间分布一个点集合，然后寻找一个向量使得所有点到这个向量的距离(即点在向量上的投影与自身的距离)之和最小。得到的这个向量能描述这个点集合的大致分布方向。

这里写图片描述

如上图，取点集合 $\{x_{1},x_{2},...,x_{n}\}$ 中的一个点 $x_{k}$ ，假设要求的方向向量为 $e$ ， $x_{k}$ 在 $e$ 上的投影为 $x_{k}^{'}$ ，则 $x_{k}$ 到 $x_{k}^{'}$ 距离的平方为 $||x_{k}^{'}-x_{k}||^2$ ，则可以得到整个点集合到向量 $e$ 的距离之和约束函数为：

\begin{aligned} J (e) & = \sum_{i = 1}^{n} | | x_{k}^{^{'}} - x_{k} | |^{2} \\ = \sum_{i = 1}^{n} | | α_{k} e - x_{k} | |^{2} \\ = \sum_{i = 1}^{n} α_{k}^{2} | | e | |^{2} - 2 \sum_{i = 1}^{n} α_{k} e^{t} x_{k} + \sum_{i = 1}^{n} | | x_{k} | |^{2} \\ = - \sum_{i = 1}^{n} α_{k}^{2} + \sum_{i = 1}^{n} | | x_{k} | |^{2} \\ = - \sum_{i = 1}^{n} e^{t} x_{k} x_{k}^{t} e + \sum_{i = 1}^{n} | | x_{k} | |^{2} \end{aligned}

$\begin{align*}J(e) &=\sum_{i=1}^{n} ||x_{k}^{'}-x_{k}||^2 \\ &= \sum_{i=1}^{n} ||\alpha_{k}e-x_{k}||^2 \\ &=\sum_{i=1}^{n} \alpha_{k}^2||e||^2-2\sum_{i=1}^{n} \alpha_{k}e^t x_{k}+\sum_{i=1}^{n} ||x_{k}||^2 \\ &=-\sum_{i=1}^n \alpha_{k}^2 + \sum_{i=1}^n||x_{k}||^2 \\ &=-\sum_{i=1}^n e^t x_{k}x_{k}^t e + \sum_{i=1}^n||x_{k}||^2 \end{align*}$
若想最小化约束函数

J (e)

$J(e)$ 则需要最大化

\sum_{i = 1}^{n} e^{t} x_{k} x_{k}^{t} e

$\sum_{i=1}^n e^t x_{k}x_{k}^t e$ ，设

S = \sum_{i = 1}^{n} x_{k} x_{k}^{t}

$S=\sum_{i=1}^n x_{k}x_{k}^t$ 则可以得到约束方程：

max_{e} e^{t} S e s . t . | | e | | = 1

$\max_{e}e^t S e \quad s.t. ||e||=1$
根据拉格朗日乘法，构造函数

L

$L$ ：

L = e^{t} S e - λ (e^{t} e - 1)

$L=e^t Se - \lambda(e^t e - 1)$
则求偏导得，

\frac{\partial L}{\partial e} = 2 S e - 2 λ e

$\frac{\partial{L}}{\partial{e}}=2Se - 2\lambda e$ ，继而得

S e = λ e

$Se=\lambda e$ ，观察发现这里正是

S

$S$ 的特征值分解。

e

$e$ 是

S

$S$ 的特征向量，对应的特征值为

e^{t} S e = λ e^{t} e = λ

$e^t S e =\lambda e^t e =\lambda$ 。这里的目标函数

max_{e} e^{t} S e = max_{e} λ

$\max_{e}e^t S e = \max_{e} \lambda$ ，即我们要取

S

$S$ 得最大特征值，以此得到主特征向量。

(3) 用python实现二维PCA简例

import numpy as np
import matplotlib.pyplot as plt

N = 10000  # 设置点的个数
s = np.array([[1, 0.8], [0.8, 1]])  # 创建一个协方差矩阵s
# print(s)
mean = (0, 0)  # 二维高斯随机分布的均值，便于计算协方差矩阵

x = np.random.multivariate_normal(mean, s, N)  # 产生两行N列的二维高斯随机序列，一行代表一个属性，每个属性有N个随机高斯数值


# 对x的协方差矩阵s进行特征值分解
a, b = np.linalg.eig(s)  # 其中a是两个特征值列表，b是两个特征向量组成的矩阵

# 取最大的特征值所对应的特征向量，返回一个坐标
dx, dy = 3 * b[:,0]

plt.style.use('ggplot')
fig = plt.figure()
ax = fig.add_subplot(111)


for spine in ['left', 'bottom']:
    ax.spines[spine].set_position('zero')  # 将坐标轴移动至原点


plt.plot(x[:, 0], x[:, 1], '.', markersize=2, alpha=0.6)  # 绘制散点图

# 在图绘制特征向量箭头
ax.arrow(0, 0, dx=dx, dy=dy, color='black', width=0.1)
ax.grid(True, color='g', linewidth=0.5, linestyle='-.')


ax.axis('equal')  # 坐标轴成正比
plt.show()

fig2 = plt.figure()
ax2 = fig2.add_subplot(111)

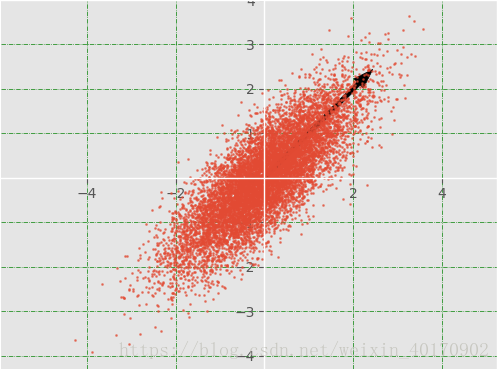
principleX = np.dot(x, b[:, 0])   # 这里计算最大特征值对应得特征向量与原始数据相乘得到一个一维数据即主成分

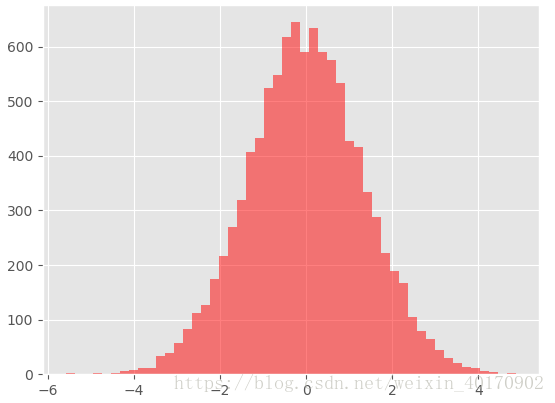
ax2.hist(principleX, 50, color='r', alpha=0.5)  # 所谓主成分即一个分布的协方差矩阵进行特征值分解，求最大的特征值所对应的特征向量，然后将该分布乘以这个特征向量得到主成分
plt.show()

运行结果：1. 主特征向量示意图；2. 主成分分布直方图
这里写图片描述

4.3 属性子集选择

属性子集选择又称特征子集选择，通过删除不相关或者冗余的属性，找出最小特征子集，使得数据类的概率分布尽可能地接近使用所有属性得到原分布。

对于 $n$ 个属性，有 $2_{n}-1$ 个可能的子集，故当 $n$ 比较大时不能用穷举法，通常使用压缩搜索空间的启发式算法(贪心算法)。“最好的”（和“最差的”）属性通常使用统计显著性检验来确定。这种检验假定属性是相互独立的。属性子集选择的启发式算法如下图示意：
这里写图片描述

4.4 回归和对数线性模型：参数化数据归约

(1) 线性回归
在线性回归中，假设两个随机变量 $x$ (自变量)和 $y$ (因变量)，假设二者满足线性关系：

y = w x + b

$y=wx+b$
其中，w和b为待定系数，假定约束函数

J (e) = \sum_{i = 1}^{n} (\hat{y_{i}} - y_{i})^{2} = \sum_{i = 1}^{n} (w x_{i} + b - y_{i})^{2}

$J(e)=\sum_{i=1}^n (\hat{y_{i}}-y_{i})^2=\sum_{i=1}^n (wx_{i}+b-y_{i})^2$ ，将

J (e)

$J(e)$ 分别对

w

$w$ 和

b

$b$ 求偏导得：

\frac{\partial J}{\partial w} = 2 \sum_{i = 1}^{n} (w x_{i} + b - y_{i}) x_{i} = 0 \frac{\partial J}{\partial b} = 2 \sum_{i = 1}^{n} (w x_{i} + b - y_{i}) = 0

$\frac{\partial J}{\partial w}=2\sum_{i=1}^n (wx_{i}+b-y_{i})x_{i}=0 \\ \frac{\partial J}{\partial b}=2\sum_{i=1}^n (wx_{i}+b-y_{i})=0$
联立两个方程可以解出：

\begin{aligned} w = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} (x_{i}^{2} - {\bar{x}}^{2})} \\ b = \bar{y} - w \bar{x} \end{aligned}

$\begin{align*} & w=\frac{\sum_{i=1}^n x_{i}y_{i} - n \bar{x} \bar{y}}{\sum_{i=1}^n (x_{i}^2-\bar{x}^2)}\\ \\ & b = \bar{y} - w \bar{x} \end{align*}$

(2) 对数线性模型(logistic逻辑回归)

逻辑回归可以参考逻辑回归(logistic regression)的本质——极大似然估计

5. 数据变换

5.1 数据规范化

原始数据的度量单位可能会影响数据分析，规范化数据赋予所有属性相等的权重。对于涉及神经网络的分类算法或基于距离度量的分类(如最邻近)和聚类，规范化特别有用。

设数值属性 $A$ 有 $n$ 个观测值 $v_{1},v_{2}, ... , v_{n}$ ，分别用以下三种方式进行规范化。

(1) 最小-最大规范化

假设 $min_A$ 和 $max_{A}$ 分别为属性 $A$ 的最小值和最大值，则最小-最大规范化计算为：

v_{i}^{^{'}} = \frac{v_{i} - m i n_{A}}{m a x_{A} - m i n_{A}} (n e w_m a x_{A} - n e w_m i n_{A}) + n e w_m i n_{A}

$v^{'}_{i}=\frac{v_{i}-min_{A}}{max_{A} - min_{A}}(new\_ max_{A}-new\_min_{A}) + new\_ min_{A}$
把

A

$A$ 的值

v_{i}

$v_{i}$ 映射到新的区间

[n e w_m a x_{A}, n e w_m i n_{A}]

$[new\_ max_{A},\ new\_ min_{A}]$ 中的

v_{i}^{^{'}}

$v_{i}^{'}$ 。

(2) z分数规范化

z分数规范化(零均值规范化)中，属性 $\bar{A}$ 的值基于 $A$ 的均值和标准差规范化。 $A$ 的值 $v_{i}$ 被规范化 $v_{i}^{'}$ ：

v_{i}^{^{'}} = \frac{v_{i} - \bar{A}}{σ_{A}}

$v_{i}^{'}=\frac{v_{i}-\bar{A}}{\sigma_{A}}$
其中，

\bar{A}

$\bar{A}$ 和

σ_{A}

$\sigma_{A}$ 分别为属性

A

$A$ 的均值和标准差。当属性

A

$A$ 的实际最小值和最大值未知，或离群点左右了最小-最大规范化时，该方法是有用的。

(3) 小数定标规范化

小数定标规范化通过移动属性 $A$ 的值的小数点位置进行规范化，小数点移动的位数依赖于 $A$ 的最大绝对值。 $A$ 的值 $v_{i}$ 被规范化为 $v_{i}^{'}$ ：

v_{i}^{^{'}} = \frac{v_{i}}{10^{j}}

$v_{i}^{'}=\frac{v_{i}}{10^j}$
其中，

j

$j$ 是使得

m a x (| v_{i}^{^{'}} |) < 1

$max(|v_{i}^{'}|)<1$ 的最小整数。

参考文献

数据挖掘概念与技术(第三版)

数据挖掘读书笔记--第三章：数据预处理