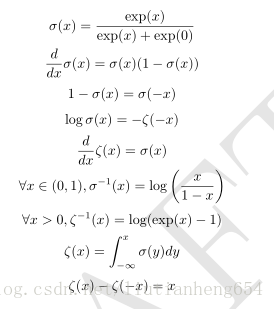概率分布
离散型变量对应概率质量函数(PMF):P。 ~表示遵从分布:x~P(x)
联合概率分布,多个变量的分布。P(x,y)
P的定义域为x所有可能技能,且P(x)位于0到1之间,且所有P(x)之和为1。
连续型变量对应概率密度函数(PDF)。此时P(x)可以大于1 。
边缘概率分布:
知道联合概率分布后求子集的分布。
离散型:
连续型:
条件概率:
主要公式:
条件概率的链式法则:
联合分布符合条件概率的链式法则。
若变量相互独立,可以表示为因子的乘积形式。
期望、方差和协方差:
期望:x由P产生时,f作用于x时,f(x)的平均值。 符合线性约束
离散型:
连续型:
方差:反应函数值变化的差异大小:体现算法的稳定性
方差的平方根为标准差。
加一部分:
何为偏差:预测值和真实值之间的差距
方差和偏差的各自使用场景:高方差对于过拟合,高偏差对应欠拟合?
bagging可以减少方差,boosting减少偏差。
协方差:两个变量线性相关性的强度和变量的尺度。
两个变量相互独立则协方差为0,协方差不为0则一定相关。
独立性要求更高,除协方差为0,还需排除非线性关系。
协方差矩阵的对角元素为方差。
常用概率分布:
均匀分布U,即x∼U(a,b)x∼U(a,b)
伯努利=0-1分布,单个二值随机变量 。
P(x = 1) =
P(x = 0) = 1-
E =
V = (1-
)
范畴分布=多项式分布,多个离散二值随机变量的任意分布 。
以上两个分布主要就是简单。
高斯分布=正态分布:
最常用的分布,主要参数均值,方差
。当均值为0,标准差为1时,称为标准正态分布。
使用精度矩阵替代原有函数,简化运算。
指数分布:在x=0处有边界点的分布。
Laplace分布:允许任一点设置为峰值。
Dirac分布:广义函数,除了某一点外其余都为0,但是积分为1,作为经验分布的一部分
经验分布:把概率密度1/m赋给m个点,使得在每个点处等分布,而且呈现Dirac分布(不扩散到其他值处)
混合分布:多种分布混合,其值取决于每一个值所对应的分布,比如GMM(高斯混合模型),是任何平滑密度函数的万能近似器 。
后验概率:知道某个之后另一个的概率 P(c|x)
常用函数:
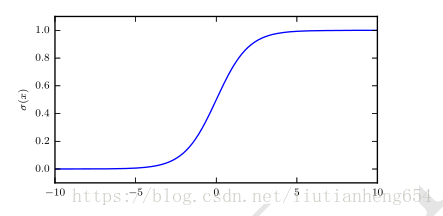
logistic sigmoid函数 :
值域在0到1,适合输出概率,但是会存在梯度饱和,对输入不再敏感。但是也常用于激活函数。
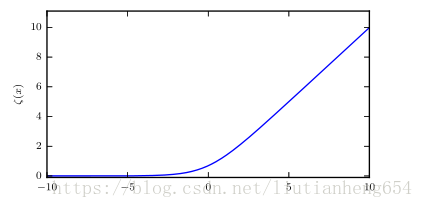
softplus函数:
类似RELU。
常用函数的有用性质:
贝叶斯法则:
。
连续型变量的技术细节:
一阶微分矩阵,又称为Jacobian矩阵。
信息论:
香农熵:整个概率中不确定性的总量。
K-L散度:相对熵。衡量两种分布之间的差异。
离散型变量下,KL散度度量Q表示P时,所需要的额外信息量。即KL越大,分布越不一致。Q的分布越不完整也可能。
非负。非对称。生成对抗网络有用,由于其不对称,可能造成。。。。
交叉熵:
结构化概率模型:
可以通过有向图和无向图表示变量间分布的互相影响。