版权声明:这些都是咸鱼Nova最后的挣扎,各位大佬转载请注明出处 https://blog.csdn.net/weixin_40883049/article/details/86829354

视觉slam十四讲学习笔记——第四章 李群与李代数
4.1 李群李代数基础
4.1.1 群
- 群的定义:群(Group)是一种集合加上一种运算的代数结构,把集合记作 ,运算记作 ·,则群记作 。
- 群的性质:
- 封闭性: .
- 结合律: .
- 幺元: .
- 逆:
- 矩阵中常见的群:
1.一般线性群 指 的可逆矩阵,它们对矩阵乘法成群。
2. 特殊正交群 也就是所谓的旋转矩阵群,其中 和 最为常见。
3. 特殊欧氏群 也就是前面提到的 维欧氏变换,如 和 。 - 李群是指具有连续(光滑)性质的群, 和 ,它们在实数空间上是连续的,所以他们都是李群。
- 每个李群都有李代数
4.2.2 李代数的引出
- 是反对称矩阵。
- 每对旋转矩阵求一次导数,左乘一个
矩阵
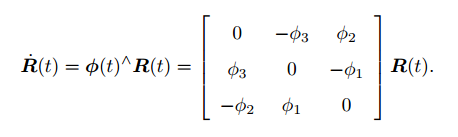
- 在 附近,有 .
4.1.3 李代数的定义
- 定义:李代数由一个集合
,一个数域
和一个二元运算
组成。如果它们满足以下几条性质,称
为一个李代数,记作
。

其中二元运算被称为李括号 - 例子,三维向量的叉积: .
4.1.4 李代数
的内容:是一个由三维向量组成的集合,每个向量对应到一个反对称矩阵,可以表达旋转矩阵的导数
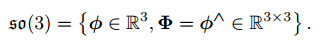
其中:
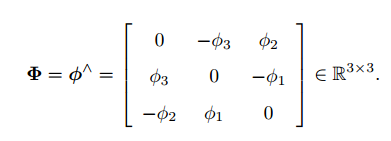
两个向量的李括号为:
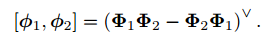
4.1.5 李代数
位于
空间中:
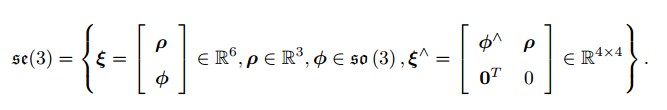
在
中,同样使用
符号,将一个六维向量转换成四维矩阵,但这里不再表示反对称。
其中李括号为:
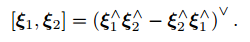
4.2 指数与对数映射
4.2.1 上的指数映射
- 计算公式:
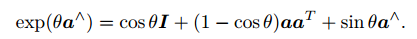
其中 。这里 是一个长度为 1 的方向向量 - 实际上就是由旋转向量组成的空间,指数映射即罗德里格斯公式,指数映射把 中任意一个向量对应到了一个位于 中的旋转矩阵。
- 通过对数映射,把
中的元素对应到
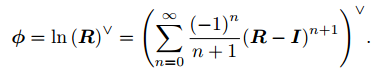
- 每个 中的元素,都可以找到一个 元素与之对应;可能存在多个 中的元素,对应到同一个 。对于旋转角 ,由周期性知,多转 360 度和没有转是同样的情况。若规定转角度固定在 之间,那么李群和李代数元素是一一对应的。
4.2.2 上的指数映射
-
上的指数映射形式如下:
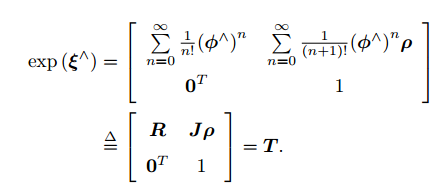
其中, 的定义如下:
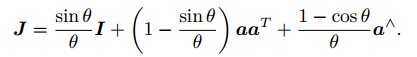
- 由变换矩阵 的表达式可知,

4.3 李代数求导与扰动模型
4.3.1 BCH 公式与近似形式
- 以下两式在变量为矩阵时不成立:
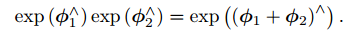
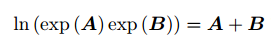
- BCH 展开式:
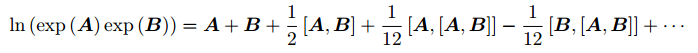
其中 为李括号 - 考虑
上的李代数
,当
或
为小量时,小量二次以上的项都可以被忽略掉。此时, BCH 拥有线性近似表达:
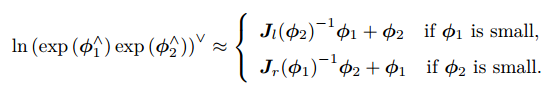
其中 的定义为:
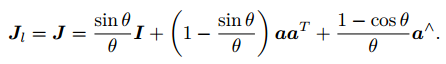
它的逆为:
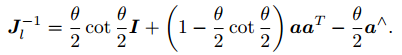
右乘雅可比矩阵对自变量变号:
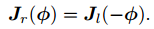
- 李群乘法与李代数加法的关系:
-
上:
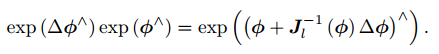
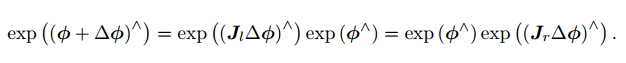
-
上:
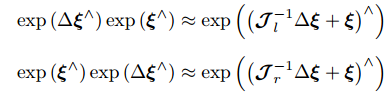
-
上:
4.3.2 李代数上的求导
- 在实践中经常会构建与位姿有关的函数,然后讨论该函数关于位姿的导数,以调整当前的估计值。
- 由于
上并没有良好定义的加法,李代数由向量组成,具有良好的加法运算。因此,使用李代数解决求导问题。思路分为两种:
- 用李代数表示姿态,然后对根据李代数加法来对李代数求导——求导模型。
- 对李群左乘或右乘微小扰动,然后对该扰动求导,称为左扰动和右扰动模型——扰动模型。
4.3.3 李代数求导
- 由于
没有加法,所以该导数无法按照导数的定义进行计算。设
对应的李代数为
,转而计算:
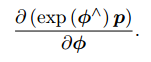
- 李代数求导公式推导:

4.3.4 扰动模型
- 扰动模型是对 进行一次扰动 。这个扰动可以乘在左边也可以乘在右边,最后结果会有一点儿微小的差异。
- 左扰动模型的推导:设左扰动
对应的李代数为
。然后,对
求导,即:
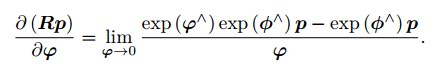
推导过程:
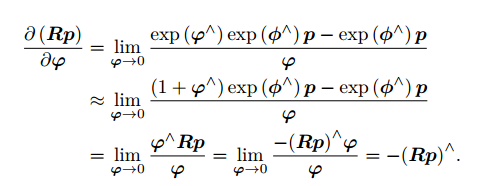
- 扰动模型省去了雅可比计算,扰动模型更为实用。
4.3.5 上的李代数求导
- 假设某空间点
经过一次变换
(对应李代数为
),得到
。现在,给
左乘一个扰动
,我们设扰动项的李代数为
,那么:

4.4 实践: Sophus
sophus github链接:https://github.com/strasdat/Sophus
4.5 *相似变换群与李代数
- 单目相机具有尺度不确定性,在计算时要显示的把尺度因子表示出来。
- 对于位于空间的点 p,在相机坐标系下经过一个相似变换,而非欧氏变换:
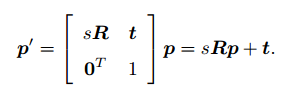
其中 为尺度因子,它同时作用在 p 的三个坐标之上,对 p 进行了一
次缩放 - 与
相似,相似变换亦对矩阵乘法构成群,称为相似变换群
:
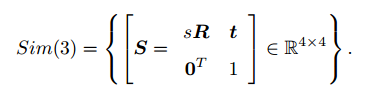
- 李代数
元素是一个七维向量
。它的前六维与
相同,最后多了一项
。
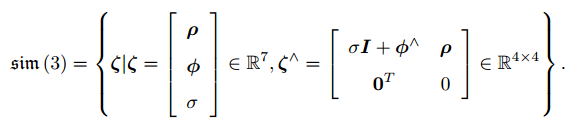
- 指数映射为:
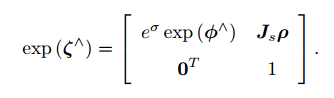
其中 的形式为:
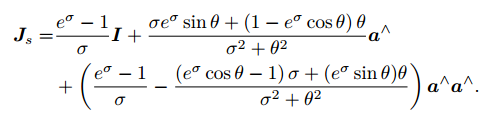
- 李代数与李群的关系为:
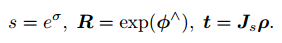
-
的扰动模型: