先明确几个概念
1.光轴:通过针孔,垂直于图像平面的线称为光轴;
2.图像中心:光轴与成像平面的交点定义为原点o1,一般位于图像中心,但由于摄像机制造误差,实际有所偏差;(这里说明了图像中心和光轴交于成像面的点会存在偏差,因此此处引出了相机的校正)
3.透视投影:物体的大小与距离的远近有关;正交投影:投影线垂直于投影面。
4.射影:描述一种数学概念;射影几何:寻找射影变换中的不变性。(更多的强调是来自哪个点,打到哪个面)
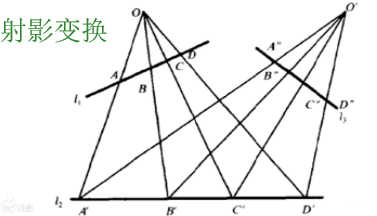
5.交比:(一个工具,来定义射影变换的不变性,射影变换,线束的交比不变)R(A,B,C,D)=R(A’,B’,C’,D’)
R(A,B,C,D)=AC/BC:AD/BD
6.仿射变换:射影变换的特例,线束为平行线束,除了交比不变,简比也不变(AC/BC=A’C’/B’C’)
上面只是科普一下,射影几何和下面研究的内容没有直接关系。
这里需要注意一点——图像坐标系的原点是由摄像机光心定义的,有时,并非图像中的中心点。
1.投影矩阵、内参、外参
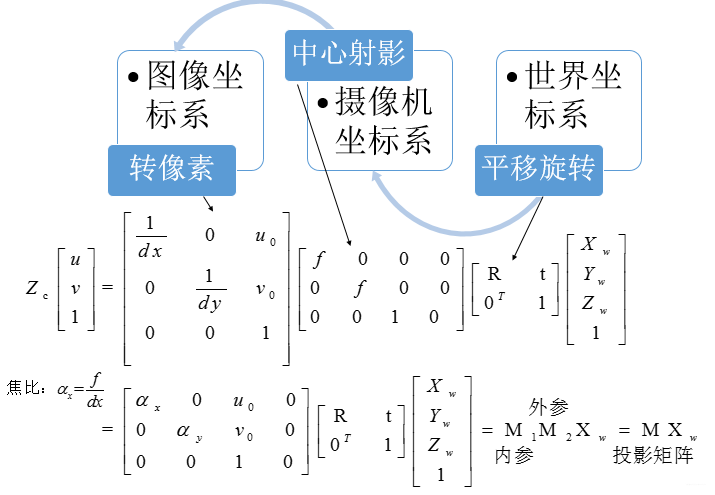
定标:相机内外参数都确定。
上面给出的公式中比较有趣的参数就是Zc,这是一个中间参数,代表在相机坐标系下,物体到相机沿光轴方向的距离。一般在求解中我们可以通过上式的三个方程消掉Zc变成两个未知数,两个方程,刚好能求解出来。然而逆着就不行了,除非我们一开始就知道了Zc,要么我们做消除,剩下两个方程,但是此时有三个未知数,因此没有确定解。

上面我们便解出了两个相机坐标的关系式,一般情况下两台相机是平行放置的。
虽然上面的方法已经解决了双目的问题,但是我们求解中,一般都是只知道投影矩阵M1和M2,而不知道R和t,因此这里就分出了两种方法
①利用矩阵分解,求出R和t(该方法可行,但是误差较大,一般不会采用,并且该方法计算量大)
②利用基本矩阵,通过M1和M2求基线
在说②方法前,我们先了解一下此处用到的一个重要的矩阵,反对称矩阵。
反对称矩阵:
设A为n维方阵,若有A’=-A,则称矩阵A为反对称矩阵。对于反对称矩阵,它的主对角线上的元素全为零,而位于主对角线两侧对称的元反号。反对称矩阵具有很多良好的性质,如若A为反对称矩阵,则A’,λA均为反对称矩阵;若A,B均为反对称矩阵,则A±B也为反对称矩阵;设A为反对称矩阵,B为对称矩阵,则AB-BA为对称矩阵;奇数阶反对称矩阵的行列式必为0。反对称矩阵的特征值是0或纯虚数,并且对应于纯虚数的特征向量的实部和虚部形成的实向量等长且互相正交。——来自百度百科
反对称——从字面理解为矩阵内部对称的位置的数是相同的,符号是相反的。

下面进行方程的推导

化简公式,将两个Zc归为一个Zc,需要右边为0,这里刚好想到了我们的
反对称矩阵性质2

这章够多的了,其实了解了就可以了,记住更好,当然,这不会影响理解双目的应用。
就像老师经常说的那句话——不用管为什么,你会用就行,当然,二郎现在需要研究机理,所以总结了这些。