信息熵的理解及推导过程

版权声明：本文为博主原创文章，欢迎转载，转载请注明出处。 https://blog.csdn.net/cjh_jinduoxia/article/details/84898574

信息熵的概述

  看过很多博客，发现大多文章只是对信息熵做了一些大致的介绍，如：信息熵代表一个随机变量的不确定性程度；也可理解为一个随机变量其值域用信息量编码后的最小码长数学期望。
  但是对于信息熵的公式为何这样，网上没有找到相关的推导过程。针对这个问题，从信息熵代表一个随机变量其值域用信息量编码后的最小码长数学期望这一物理意义入手，本文使用最优化的方法，对信息熵公式进行了推导。过程中难免存在数学上的严谨性问题，欢迎各位指正。
  随机变量分为离散型和连续型两种，本文仅对离散型变量进行讨论，关于连续型，其原理也是大同小异。

离散型随机变量的信息熵公式

  设离散型随机变量X的值域为 $\{x_1,x_2,...,x_i,...x_n\}$，其取值为 $x_i$时的概率为 $p_i$，则其信息熵为：
$H\left(X\right)=\sum_{i=1}^{n}p_i \log_b \frac{1}{p_i}$
  上面公式中，常取b=2，主要是因为计算机编码中常用二进制编码，所以本文也是采用b=2进行讨论。下面谈谈对这个公式的理解。

信息熵公式理解

  我们不妨先思考一个问题：假设离散型随机变量X的所有状态为 $\{x_1,x_2,...,x_i,...x_n\}$，当状态为 $x_i$时的概率为 $p_i$，那么使用二进制进行编码，设每个状态 $x_i$的最终编码长度为 $l_i$，那么 $l_i$分别是多长，才能使得最终的平均编码长度最小（即前面说的码长期望值最小），也即使得下面公式最小：
$L=p_1l_1+p_2l_2+...+p_nl_n$
  实际上解决了上面的问题后，最终会发现 $L_{min}=H\left(X\right)$，即最小的码长期望值，实际上就是随机变量X的信息熵。

编码的约束条件

  首先，针对上面的求最小化问题，我们仅仅是将其要优化的目标函数写出来而已，现在需要将此优化问题的条件补全，呈现出完整的最优化方程进行求解。
  我们要使平均码长最小，当然会想到使得每个 $l_i$最小（最好都等于1），那么这个平均长度自然最小。但是对应状态数大于2的随机变量X来说，这显然不可能，因为如果每个状态的编码长度为1（即编码是0或1），那么最多可以表示2个状态，其余状态无法表示。所以在编码长度方面，存在着一定的限制条件，此即为我们要找的最优化方程的限制条件。下面讨论一下关于编码的限制条件：

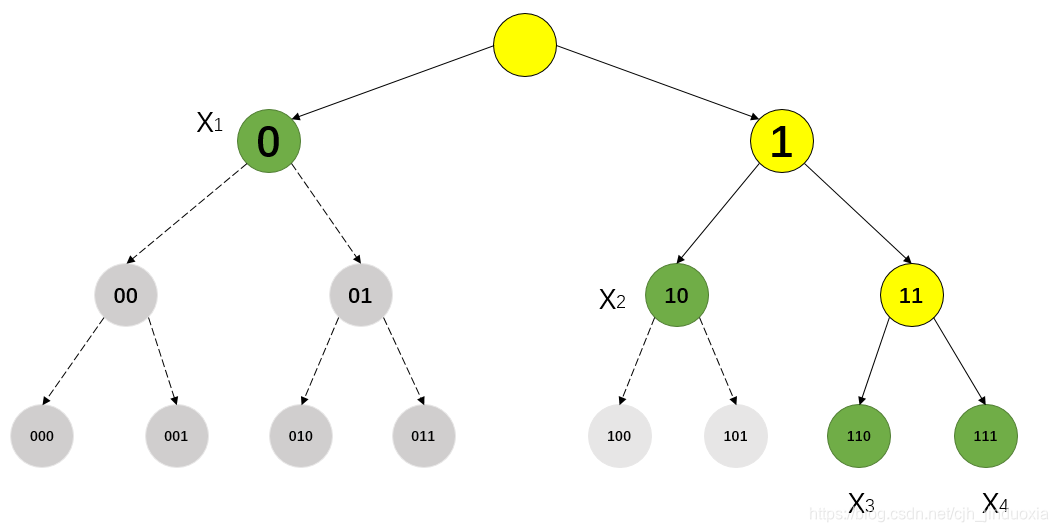
1. 假设用二进制表示随机变量X（X的所有状态为 $\{x_1,x_2,x_3,x_4\}$），其编码长度不要求相同。如上图所示，假设可用的码长最长为3，所以上图中最多能代表的状态数为 $2^3=8$，现在只要编码4个状态，所以可以个状态的码长均为2（用00，01，10，11分别代表4个状态），也可以使用如上图所示的编码（图中黄色节点表示该节点还未被编码，绿色节点表示该节点已经被用于编码，灰色节点表示不能再被用于编码），当然也可以用其他的编码方式。但是无论如何进行编码，都要符合这个条件：母节点的编码被使用后，其下面所有的字节点编码均不能再使用，不然会导致编码重复，无法实现编码的单一性。如：用编码0来代表 $x_1$，则0下面的字节点 $00,01,...,011$均不能为其他状态使用（比如，假设有3个状态其编码分别为0，1，01，则在使用中，如果出现01编码，无法判断它是代表的哪个状态，其有可能是01单个状态，也有可能是0、1两个一前一后的状态。）
2. 现假设最长的编码长度为 $l_X$，则理论上可以编码表示 $2^{l_X}$个可能状态，但是对于编码为0的状态，显然它一个状态就占用了人家 $2^{l_X-1}$种可能状态的坑。显然，对于某一状态 $x_i$，其编码长度为 $l_{x_i}$，则就这一个状态就占用了一共 $2^{l_X-l_{x_i}}$种可能状态的坑。前面说过，最长的编码长度为 $l_X$，则理论上只有 $2^{l_X}$种可能状态坑，而且各个状态的坑之间不能有重叠（不然无法保证单一性，最后无法辨别，前面1中有说），所以就有下面这个约束条件：
   $\sum_{i=1}^{n}2^{l_X-l_{x_i}} \leq 2^{l_X} \Longrightarrow \frac{1}{2^{l_1}}+\frac{1}{2^{l_2}}+...+\frac{1}{2^{l_n}} \leq 1$

信息熵公式的推导

  经过前面的介绍，我们现在可以将上面提到的最小编码期望值问题，表示成一个最优化方程的求解问题了。
  问题描述： 对于随机变量X，其所有的可能状态为 $\left\{x_1,x_2,...,x_n\right\}$，各个状态出现的概率分别为 $\left\{p_1,p_2,...,p_n\right\}$，现假设每个状态的编码长度为 $\left\{l_1,l_2,...,l_n\right\}$，其中 $l_i \in Z^+$，求最短的平均编码长度，于是可以列出以下最优化式子：
$\begin{cases} min & p_1l_1+p_2l_2+...+p_nl_n\\ s.t. & \frac{1}{2^{l_1}}+\frac{1}{2^{l_2}}+...+\frac{1}{2^{l_n}} \leq 1 \\ & l_i \geq 0\ and\ l_i \in Z^+,\ \ 1\leq i \leq n \end{cases}$
  显然，平常的编码长度只能是整数问题，所以上面的式子是整数优化问题。但是对于更一般的问题，可以不局限于码长是整数，所以这里将码长为整数这一限制去除，得到下面的优化方程：
$\begin{cases} min & p_1l_1+p_2l_2+...+p_nl_n\\ s.t. & \frac{1}{2^{l_1}}+\frac{1}{2^{l_2}}+...+\frac{1}{2^{l_n}} \leq 1 \\ & l_i \geq 0,\ \ 1\leq i \leq n \end{cases}$
  不妨令 $l^{'}_i=-l_i$，则可以化简为
$\begin{cases} min & -\left(p_1l^{'}_1+p_2l^{'}_1+...+p_nl^{'}_1\right)\\ s.t. & 2^{l^{'}_1}+2^{l^{'}_2}+...+2^{l^{'}_n} \leq 1 \\ & l^{'}_i \leq 0,\ \ 1\leq i \leq n \end{cases}$
  再令 $I_i=2^{l^{'}_i}$，可得：
$\begin{cases} min & -\left(p_1\log_2I_1+p_2\log_2I_2+...p_n\log_2I_n\right)\\ s.t. & I_1+I_2+...+I_n\leq1\\ & 0\leq I_i,\ \ 1\leq i \leq n \end{cases}$
  现在假设设取到最优解 $\left\{I^{'}_1,I^{'}_2,...,I^{'}_n\right\}$时，上式约束条件的等号不成立，即： $I^{'}_1+I^{'}_2+...+I^{'}_n<1$，也即有： $I^{'}_1+I^{'}_2+...+I^{'}_n+I^{'}_x=1,while\ I^{'}_x>0$，则可知 $\left\{I^{'}_1,I^{'}_2,...I^{''}_i,...,I^{'}_n\right\},while\ I^{''}_i=I^{'}_i+I_x$，也是其中的一个解，而且显然该解比原先的解更好（使得目标函数更小）。由此可知，当取得最优解时，上式中的约束条件 $I_1+I_2+...+I_n\leq1$ 一定等号成立，现将其代入表达式可以求解得到最优解。
  将 $I_1+I_2+...+I_n=1 \Longrightarrow I_n=1-\sum_{i=1}^{n-1}I_i$代入原最优化式子中，有：
$\begin{cases} min & -\left[p_1\log_2I_1+p_2\log_2I_2+...+p_{n-1}\log_2I_{n-1}+p_n\log_2\left({1-\sum_{i=1}^{n-1}I_i}\right)\right]\\ s.t & 0\leq I_i \leq 1,\ \ 1\leq i \leq n-1 \end{cases}$
  当取最小值时，对 $I_1,I_2,...,I_{n-1}$求偏导则均为0，有：
$\begin{cases} \frac{p_1}{I_1\ln 2}-\frac{p_n}{\left({1-\sum_{i=1}^{n-1}I_i}\right)\ln 2}=0 \\ ... \\ \frac{p_{n-1}}{I_{n-1}\ln 2}-\frac{p_n}{\left({1-\sum_{i=1}^{n-1}I_i}\right)\ln 2}=0 \end{cases}$
  经过化简可得：
$\begin{cases} p_1\left(1-I_1-...-I_{n-1}\right)=p_1I_n=p_nI_1 \Longrightarrow \frac{I_1}{p_1}=\frac{I_n}{p_n}\\ ...\\ p_{n-1}\left(1-I_1-...-I_{n-1}\right)=p_{n-1}I_n=p_nI_{n-1} \Longrightarrow \frac{I_{n-1}}{p_{n-1}}=\frac{I_n}{p_n} \end{cases}$
$\Longrightarrow \frac{I_1}{p_1} = \frac{I_2}{p_2} = ... = \frac{I_{n-1}}{p_{n-1}} = \frac{I_n}{p_n} ，while \ \sum_{i=1}^{n}I_i=\sum_{i=1}^{n}p_i=1$
  即最优解为： $I_1=p_1,I_2=p_2,...,I_n=p_n$，也即 $l_1=-\log_2I_1=-\log_2p_1, l_2=-\log_2I_2=-\log_2p_2,...,l_n=-\log_2I_n=-\log_2p_n$。
  代入原式，则最短的平均编码长度为： $H\left(X\right)=\sum_{i=1}^{n}p_i \log_2 \frac{1}{p_i}$，此式和信息熵的公式完全相同，上面的推导便也可看成是信息熵的一种推导过程。
  最后，对于信息熵的物理意义，我们可以这样进行理解：对于一个随机变量X，其各个状态出现的概率不同，我们要对其进行编码，所求得的最短平均编码长度便为信息熵。