本章, 我们开启对求解一般约束优化问题
min
x
∈
R
n
f
(
x
)
,
s
u
b
j
e
c
t
 
t
o
 
c
i
(
x
)
=
0
,
i
∈
E
,
c
i
(
x
)
≥
0
,
i
∈
I
\min_{x\in\mathbb{R}^n}f(x),\quad\mathrm{subject\,to\,}\begin{array}{ll}c_i(x)=0, & i\in\mathcal{E},\\c_i(x)\ge0, & i\in\mathcal{I}\end{array}
x ∈ R n min f ( x ) , s u b j e c t t o c i ( x ) = 0 , c i ( x ) ≥ 0 , i ∈ E , i ∈ I 算法的讨论, 这里目标函数
f
f
f 、约束函数
c
i
c_i
c i 均是
R
n
\mathbb{R}^n
R n 子集上的
光滑实值函数 ,
I
,
E
\mathcal{I},\mathcal{E}
I , E 分别是不等式和等式约束的有限指标集. 在
第十二章 , 我们使用这一一般形式推导了问题的
最优性条件 . 这是本书剩下各类算法的
核心动机 . 它们尽管各自不同, 但本质上都是
迭代方法 : 它们都是产生解
x
∗
x^*
x ∗ 的一串估计序列, 而我们期望序列能收敛到解. 在某些情形下, 它们也产生对Lagrange乘子的估计序列. 如同在无约束优化中, 我们仅考虑求问题局部解的算法.
本章我们并不纠结于某个算法的推导, 而是企图建立基本的概念、搭建普遍的框架. 在阅读完第1,2节后, 读者可以一瞥第3-6节中的材料与示例. 在接下来几个章节的学习中, 读者可以回过头来利用这些例子进行学习.
我们现在罗列本书剩下部分的算法. 对于非线性优化算法, 现在还没有标准的分类方式. 但在接下来的章节中, 我们按如下方式分类归总讲述:
第十六章中我们讨论求解二次规划quadratic programming 问题的算法. 我们将这一类算法单独拎出来主要是因为其本身相当重要 :
二次规划问题本身具有独特的性质, 基于此可以设计高效的算法;
在逐步二次规划算法和某些非线性规划内点法中我们需要求解二次规划子问题, 这为后续的讨论作铺垫.
第十七章中我们讨论罚函数和增广Lagrange函数(penalty and augmented Lagrangian)法 .
结合目标函数和约束函数 , 我们可以构建罚函数(penalty function)并以求解一系列无约束问题代替求解原本的约束问题. 例如, 若原始问题中仅有等式约束, 我们就可以定义二次罚函数 为
f
(
x
)
+
μ
2
∑
i
∈
E
c
i
2
(
x
)
,
f(x)+\frac{\mu}{2}\sum_{i\in\mathcal{E}}c_i^2(x),
f ( x ) + 2 μ i ∈ E ∑ c i 2 ( x ) ,
μ
>
0
\mu>0
μ > 0 惩罚因子(penalty paramater) . 我们将对不断增大的
μ
\mu
μ 使用精确罚函数(exact penalty function) , 我们就可以仅通过求解单个 无约束问题得到原始约束问题的局部解. 例如对等式约束问题, 我们定义函数
f
(
x
)
+
μ
∑
i
E
∣
c
i
(
x
)
∣
,
μ
>
0
充
分
大
f(x)+\mu\sum_{i\mathbb{E}}|c_i(x)|, \mu>0充分大
f ( x ) + μ i E ∑ ∣ c i ( x ) ∣ , μ > 0 充 分 大 可用一系列光滑的子问题逼近 得到极小.
在增广Lagrange函数法 中, 我们定义一个结合了Lagrange函数和二次惩罚函数性质的函数 , 称作增广Lagrange函数. 对于等式约束问题, 它具有以下形式:
L
A
(
x
,
λ
;
μ
)
=
f
(
x
)
−
∑
i
∈
E
λ
i
c
i
(
x
)
+
μ
2
∑
i
∈
E
c
i
2
(
x
)
.
\mathcal{L}_A(x,\lambda;\mu)=f(x)-\sum_{i\in\mathcal{E}}\lambda_ic_i(x)+\frac{\mu}{2}\sum_{i\in\mathcal{E}}c_i^2(x).
L A ( x , λ ; μ ) = f ( x ) − i ∈ E ∑ λ i c i ( x ) + 2 μ i ∈ E ∑ c i 2 ( x ) .
λ
\lambda
λ
μ
\mu
μ
L
A
(
⋅
,
λ
;
μ
)
\mathcal{L}_A(\cdot,\lambda;\mu)
L A ( ⋅ , λ ; μ )
x
x
x
λ
,
μ
\lambda,\mu
λ , μ 能避免二次惩罚函数带来的一些问题 .
第十八章中我们介绍逐步二次规划sequential quadratic programming, SQP 算法. 本质上, 它们在每个迭代点都对问题构建一个二次规划子问题并定义搜索方向为此子问题的解. 基本的SQP算法中, 我们定义
(
x
k
,
λ
k
)
(x_k,\lambda_k)
( x k , λ k )
p
k
p_k
p k
min
p
1
2
p
T
∇
x
x
2
L
(
x
k
,
λ
k
)
p
+
∇
f
(
x
k
)
T
p
s
u
b
j
e
c
t
 
t
o
∇
c
i
(
x
k
)
T
p
+
c
i
(
x
k
)
=
0
,
i
∈
E
,
∇
c
i
(
x
k
)
T
p
+
c
i
(
x
k
)
≥
0
,
i
∈
I
,
\begin{array}{rl}\min_p &\frac{1}{2}p^T\nabla^2_{xx}\mathcal{L}(x_k,\lambda_k)p+\nabla f(x_k)^Tp\\\mathrm{subject\,to}&\nabla c_i(x_k)^Tp+c_i(x_k)=0,\quad i\in\mathcal{E},\\&\nabla c_i(x_k)^Tp+c_i(x_k)\ge0,\quad i\in\mathcal{I},\end{array}
min p s u b j e c t t o 2 1 p T ∇ x x 2 L ( x k , λ k ) p + ∇ f ( x k ) T p ∇ c i ( x k ) T p + c i ( x k ) = 0 , i ∈ E , ∇ c i ( x k ) T p + c i ( x k ) ≥ 0 , i ∈ I ,
L
\mathcal{L}
L
x
k
x_k
x k
x
k
+
p
x_k+p
x k + p 信赖域约束 控制
p
p
p 拟牛顿近似 Hessian阵可用来代替
∇
x
x
2
L
(
x
k
,
λ
k
)
\nabla^2_{xx}\mathcal{L}(x_k,\lambda_k)
∇ x x 2 L ( x k , λ k ) 逐步线性-二次规划(sequential linear-quadratic programming) , 其
p
k
p_k
p k
第十九章, 我们讨论非线性规划的内点法(interior-point methods for nonlinear programming) . 这些方法可视作第十四章 线性规划原始-对偶内点法的延伸. 我们也可以将它们视作障碍函数法(barrier methods) , 其中搜索方向通过求解以下以障碍函数作为目标函数的问题获得(这里以对数障碍函数为例):
min
x
,
s
f
(
x
)
−
μ
∑
i
=
1
m
log
s
i
s
u
b
j
e
c
t
 
t
o
c
i
(
x
)
=
0
,
i
∈
E
,
c
i
(
x
)
−
s
i
=
0
,
i
∈
I
,
\begin{array}{rl}\min\limits_{x,s} & f(x)-\mu\sum\limits_{i=1}^m\log s_i\\\mathrm{subject\,to} & c_i(x)=0,\quad i\in\mathcal{E},\\& c_i(x)-s_i=0,\quad i\in\mathcal{I},\end{array}
x , s min s u b j e c t t o f ( x ) − μ i = 1 ∑ m log s i c i ( x ) = 0 , i ∈ E , c i ( x ) − s i = 0 , i ∈ I , 障碍因子(barrier parameter)
μ
>
0
\mu>0
μ > 0
s
i
>
0
s_i>0
s i > 0 松弛变量 . 内点法是时下非线性规划的最新研究热点, 并已成为逐步二次规划算法的重要竞争对手.
在第1,3,4类中的算法均使用了消元技术(elimination techniques) , 即利用约束消去了问题中的自由度. 为方便后续, 我们在第3节讨论消元. 而在之后的小节中, 我们介绍价值函数(merit functions)和 滤子(filters) . 它们对于非线性规划算法的全局收敛性具有重要意义.
求解非线性规划问题的主要困难之一在于处理不等式约束 , 特别地, 是决定这些约束在解处是否起作用 . 积极集法的本质方法就是首先对最优积极集
A
∗
\mathcal{A}^*
A ∗ 工作集(working set) , 记为
W
\mathcal{W}
W
W
\mathcal{W}
W
W
\mathcal{W}
W
x
∗
x^*
x ∗
但是工作集
W
\mathcal{W}
W ——至多到
2
∣
I
∣
2^{|\mathcal{I}|}
2 ∣ I ∣
∣
I
∣
|\mathcal{I}|
∣ I ∣ 组合困难 ——我们不能设计出考虑所有
W
\mathcal{W}
W
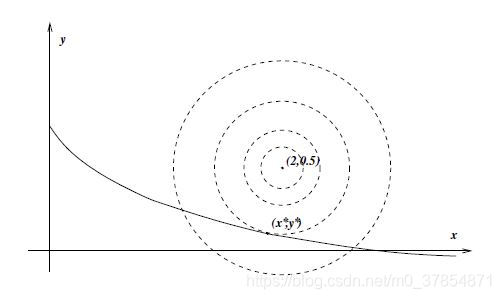
例1 考虑问题
min
x
,
y
f
(
x
,
y
)
=
d
e
f
1
2
(
x
−
2
)
2
+
1
2
(
y
−
1
2
)
2
s
u
b
j
e
c
t
 
t
o
(
x
+
1
)
−
1
−
y
−
1
4
≥
0
,
x
≥
0
,
y
≥
0.
\begin{array}{rl}\min\limits_{x,y}&f(x,y)\xlongequal{def}\frac{1}{2}(x-2)^2+\frac{1}{2}(y-\frac{1}{2})^2\\\mathrm{subject\,to} &(x+1)^{-1}-y-\frac{1}{4}\ge0,\\&x\ge0,\\&y\ge0.\end{array}
x , y min s u b j e c t t o f ( x , y ) d e f
2 1 ( x − 2 ) 2 + 2 1 ( y − 2 1 ) 2 ( x + 1 ) − 1 − y − 4 1 ≥ 0 , x ≥ 0 , y ≥ 0 .
由图中可知, 在解
(
x
∗
,
y
∗
)
T
=
(
1.953
,
0.089
)
T
(x^*,y^*)^T=(1.953,0.089)^T
( x ∗ , y ∗ ) T = ( 1 . 9 5 3 , 0 . 0 8 9 ) T
W
\mathcal{W}
W
2
3
=
8
2^3=8
2 3 = 8
解处无约束积极, 即
W
=
∅
\mathcal{W}=\empty
W = ∅
∇
f
=
(
x
−
2
,
y
−
1
/
2
)
T
\nabla f=(x-2,y-1/2)^T
∇ f = ( x − 2 , y − 1 / 2 ) T
f
f
f
解处三个约束都积极, 即
W
=
{
1
,
2
,
3
}
\mathcal{W}=\{1,2,3\}
W = { 1 , 2 , 3 }
W
=
{
2
}
\mathcal{W}=\{2\}
W = { 2 }
x
=
0
x=0
x = 0
f
f
f
(
0
,
1
/
2
)
T
(0,1/2)^T
( 0 , 1 / 2 ) T
W
=
{
1
,
3
}
\mathcal{W}=\{1,3\}
W = { 1 , 3 }
(
3
,
0
)
T
(3,0)^T
( 3 , 0 ) T
λ
2
=
0
\lambda_2=0
λ 2 = 0
λ
1
=
−
16
,
λ
3
=
−
16.5
\lambda_1=-16,\lambda_3=-16.5
λ 1 = − 1 6 , λ 3 = − 1 6 . 5
W
=
{
1
}
\mathcal{W}=\{1\}
W = { 1 }
(
x
,
y
)
T
=
(
1.953
,
0.089
)
T
(x,y)^T=(1.953,0.089)^T
( x , y ) T = ( 1 . 9 5 3 , 0 . 0 8 9 ) T
λ
1
=
0.411
,
λ
2
=
λ
3
=
0
\lambda_1=0.411,\lambda_2=\lambda_3=0
λ 1 = 0 . 4 1 1 , λ 2 = λ 3 = 0
对于这一个小例子, 我们也能发现考虑所有可能的工作集选择相当耗时耗力 . 但上图表明, 某些
W
\mathcal{W}
W 可用关于函数和导数的信息去除 . 事实上, 第十六章的积极集法就是利用这样的信息对最优积极集作一系列估计, 避免显然不是最优积极集的
W
\mathcal{W}
W
一种不同的方式是第十九章中的内点(或障碍函数)法. 这些方法产生远离由不等式约束界定的可行域边界的迭代点. 随着算法逐渐趋近解, 障碍的效果将会减弱, 从而保证估计的精度. 这样, 内点法就避免了非线性规划的组合困难 .
在处理带约束的优化问题时, 一个很自然的想法是用约束减少问题的变量个数、降低自由度, 得到更简单的问题 . 不过, 消元技术必须小心使用, 因为它们可能会改变会改变问题或者让问题变得病态.
我们先以一个简单的例子开头. 对它来说, 消元是安全且便捷的.
min
f
(
x
)
=
f
(
x
1
,
x
2
,
x
3
,
x
4
)
,
s
u
b
j
e
c
t
 
t
o
 
x
1
+
x
3
2
−
x
4
x
3
=
0
,
−
x
2
+
x
4
+
x
3
2
=
0.
\min f(x)=f(x_1,x_2,x_3,x_4),\quad\mathrm{subject\,to\,}\begin{array}{l}x_1+x_3^2-x_4x_3=0,\\-x_2+x_4+x_3^2=0.\end{array}
min f ( x ) = f ( x 1 , x 2 , x 3 , x 4 ) , s u b j e c t t o x 1 + x 3 2 − x 4 x 3 = 0 , − x 2 + x 4 + x 3 2 = 0 .
x
1
=
x
4
x
3
−
x
3
2
,
x
2
=
x
4
+
x
3
2
,
x_1=x_4x_3-x_3^2,\quad x_2=x_4+x_3^2,
x 1 = x 4 x 3 − x 3 2 , x 2 = x 4 + x 3 2 ,
h
(
x
3
,
x
4
)
=
f
(
x
4
x
3
−
x
3
2
,
x
4
+
x
3
2
,
x
3
,
x
4
)
,
h(x_3,x_4)=f(x_4x_3-x_3^2,x_4+x_3^2,x_3,x_4),
h ( x 3 , x 4 ) = f ( x 4 x 3 − x 3 2 , x 4 + x 3 2 , x 3 , x 4 ) ,
非线性消元的危害 则以下例说明.
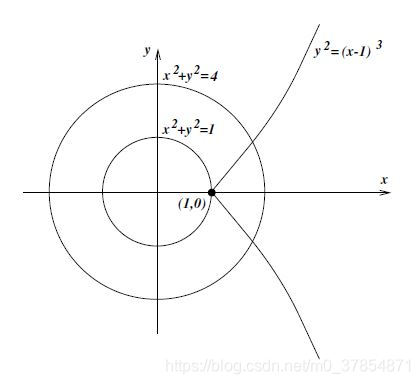
例2 考虑问题
min
x
2
+
y
2
,
s
u
b
j
e
c
t
 
t
o
 
(
x
−
1
)
3
=
y
2
.
\min x^2+y^2,\quad\mathrm{subject\,to\,}(x-1)^3=y^2.
min x 2 + y 2 , s u b j e c t t o ( x − 1 ) 3 = y 2 .
(
x
,
y
)
=
(
1
,
0
)
(x,y)=(1,0)
( x , y ) = ( 1 , 0 )
利用约束消去
y
y
y
h
(
x
)
=
x
2
+
(
x
−
1
)
3
.
h(x)=x^2+(x-1)^3.
h ( x ) = x 2 + ( x − 1 ) 3 .
h
(
x
)
→
−
∞
(
x
→
−
∞
)
h(x)\to-\infty(x\to-\infty)
h ( x ) → − ∞ ( x → − ∞ )
(
x
−
1
)
3
=
y
2
(x-1)^3=y^2
( x − 1 ) 3 = y 2
x
≥
1
x\ge1
x ≥ 1
y
y
y
x
≥
1
x\ge1
x ≥ 1
此例表明使用非线性方程组消元可能导致不可逆转的后果 . 基于此, 大多数优化算法并不使用非线性消元, 而是先对约束做线性化再对简化的问题消元 . 下面我们系统地介绍下如何用线性约束消元.
现考虑带线性等式约束的非线性目标极小化问题:
min
f
(
x
)
,
s
u
b
j
e
c
t
 
t
o
 
A
x
=
b
,
\min f(x),\quad\mathrm{subject\,to\,}Ax=b,
min f ( x ) , s u b j e c t t o A x = b ,
A
A
A
m
×
n
:
m
≤
n
m\times n:m\le n
m × n : m ≤ n
A
A
A
A
A
A
m
m
m
m
×
m
m\times m
m × m
B
B
B
n
×
n
n\times n
n × n
P
P
P
A
A
A
m
m
m
A
P
=
[
B
∣
N
]
,
AP=[B\mid N],
A P = [ B ∣ N ] ,
N
N
N
A
A
A
n
−
m
n-m
n − m
x
B
∈
R
m
,
x
N
∈
R
n
−
m
x_B\in\mathbb{R}^m,x_N\in\mathbb{R}^{n-m}
x B ∈ R m , x N ∈ R n − m
[
x
B
x
N
]
=
P
T
x
,
\begin{bmatrix}x_B\\x_N\end{bmatrix}=P^Tx,
[ x B x N ] = P T x ,
x
B
x_B
x B
B
B
B
P
P
T
=
I
PP^T=I
P P T = I
b
=
A
x
=
A
P
(
P
T
x
)
=
B
x
B
+
N
x
N
.
b=Ax=AP(P^Tx)=Bx_B+Nx_N.
b = A x = A P ( P T x ) = B x B + N x N .
x
B
=
B
−
1
b
−
B
−
1
N
x
N
.
x_B=B^{-1}b-B^{-1}Nx_N.
x B = B − 1 b − B − 1 N x N . 简单消元(simple elimination of variables) . 这样对任意
x
N
x_N
x N
min
x
N
h
(
x
N
)
=
d
e
f
f
(
P
[
B
−
1
b
−
B
−
1
N
x
N
x
N
]
)
.
\min\limits_{x_N}h(x_N)\xlongequal{def}f\left(P\begin{bmatrix}B^{-1}b-B^{-1}Nx_N\\x_N\end{bmatrix}\right).
x N min h ( x N ) d e f
f ( P [ B − 1 b − B − 1 N x N x N ] ) . 等价于一个无约束问题 .
例3 考虑问题
min
sin
(
x
1
+
x
2
)
+
x
3
2
+
1
3
(
x
4
+
x
5
4
+
x
6
/
2
)
s
u
b
j
e
c
t
 
t
o
8
x
1
−
6
x
2
+
x
3
+
9
x
4
+
4
x
5
=
6
,
3
x
1
+
2
x
2
−
x
4
+
6
x
5
+
4
x
6
=
−
4.
\begin{array}{rl}\min & \sin(x_1+x_2)+x_3^2+\frac{1}{3}(x_4+x_5^4+x_6/2)\\\mathrm{subject\,to} & 8x_1-6x_2+x_3+9x_4+4x_5=6,\\&3x_1+2x_2-x_4+6x_5+4x_6=-4.\end{array}
min s u b j e c t t o sin ( x 1 + x 2 ) + x 3 2 + 3 1 ( x 4 + x 5 4 + x 6 / 2 ) 8 x 1 − 6 x 2 + x 3 + 9 x 4 + 4 x 5 = 6 , 3 x 1 + 2 x 2 − x 4 + 6 x 5 + 4 x 6 = − 4 .
P
P
P
P
x
=
[
x
3
x
6
x
1
x
2
x
4
x
5
]
,
A
P
=
[
1
0
∣
8
−
6
9
4
0
4
∣
3
2
−
1
6
]
.
Px=\begin{bmatrix}x_3\\x_6\\x_1\\x_2\\x_4\\x_5\end{bmatrix},\quad AP=\left[\begin{array}{ccccccc}1 & 0 & \mid & 8 & -6 & 9 & 4\\0 & 4 & \mid & 3 & 2 & -1 & 6\end{array}\right].
P x = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ x 3 x 6 x 1 x 2 x 4 x 5 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ , A P = [ 1 0 0 4 ∣ ∣ 8 3 − 6 2 9 − 1 4 6 ] .
B
B
B
[
x
3
x
6
]
=
−
[
8
−
6
9
4
3
4
1
2
−
1
4
3
2
]
[
x
1
x
2
x
4
x
5
]
+
[
6
−
1
]
.
\begin{bmatrix}x_3\\x_6\end{bmatrix}=-\begin{bmatrix}8 & -6 & 9 & 4\\\frac{3}{4} & \frac{1}{2} & -\frac{1}{4} & \frac{3}{2}\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_4\\x_5\end{bmatrix}+\begin{bmatrix}6\\-1\end{bmatrix}.
[ x 3 x 6 ] = − [ 8 4 3 − 6 2 1 9 − 4 1 4 2 3 ] ⎣ ⎢ ⎢ ⎡ x 1 x 2 x 4 x 5 ⎦ ⎥ ⎥ ⎤ + [ 6 − 1 ] .
x
3
,
x
6
x_3,x_6
x 3 , x 6
min
x
1
,
x
2
,
x
4
,
x
5
sin
(
x
1
+
x
2
)
+
(
8
x
1
−
6
x
2
+
9
x
4
+
4
x
5
−
6
)
2
+
1
3
(
x
4
+
x
5
4
−
[
(
1
/
2
)
+
(
3
/
8
)
x
1
+
(
1
/
4
)
x
2
−
(
1
/
8
)
x
4
+
(
3
/
4
)
x
5
]
)
.
\begin{array}{rl}\min\limits_{x_1,x_2,x_4,x_5} & \sin(x_1+x_2)+(8x_1-6x_2+9x_4+4x_5-6)^2\\&+\frac{1}{3}(x_4+x_5^4-[(1/2)+(3/8)x_1+(1/4)x_2-(1/8)x_4+(3/4)x_5]).\end{array}
x 1 , x 2 , x 4 , x 5 min sin ( x 1 + x 2 ) + ( 8 x 1 − 6 x 2 + 9 x 4 + 4 x 5 − 6 ) 2 + 3 1 ( x 4 + x 5 4 − [ ( 1 / 2 ) + ( 3 / 8 ) x 1 + ( 1 / 4 ) x 2 − ( 1 / 8 ) x 4 + ( 3 / 4 ) x 5 ] ) .
A
A
A
B
−
1
N
B^{-1}N
B − 1 N
一般, 我们可通过Gauss消去法选取
m
m
m
B
B
B
B
B
B 稀疏Gauss消去法 . 它会在控制舍入误差的同时保留稀疏性. 这一算法的实施可用HSL库中的MA48. 但下面我们会说明, Gauss消去过程不能保证能够选取最佳的基矩阵 .
简单消元法有一个有趣的解释. 为简化记号, 假设基矩阵就是
A
A
A
m
m
m
P
=
I
P=I
P = I
[
x
B
x
N
]
=
x
=
Y
b
+
Z
x
N
,
\begin{bmatrix}x_B\\x_N\end{bmatrix}=x=Yb+Zx_N,
[ x B x N ] = x = Y b + Z x N ,
Y
=
[
B
−
1
O
]
,
Z
=
[
−
B
−
1
N
I
]
.
Y=\begin{bmatrix}B^{-1}\\O\end{bmatrix},\quad Z=\begin{bmatrix}-B^{-1}N\\I\end{bmatrix}.
Y = [ B − 1 O ] , Z = [ − B − 1 N I ] .
Z
Z
Z
A
Z
=
O
AZ=O
A Z = O
Z
Z
Z
A
A
A
Y
,
Z
Y, Z
Y , Z
Y
b
Yb
Y b
A
x
=
b
Ax=b
A x = b
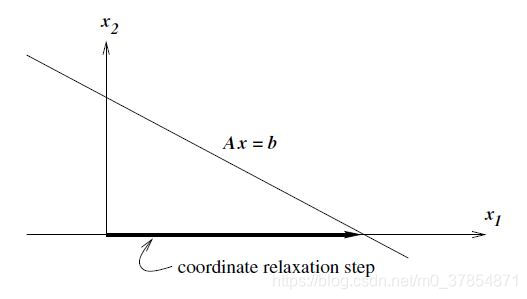
换句话说, 简单消元法将可行点表示成
A
x
=
b
Ax=b
A x = b
A
A
A . 特解
Y
b
Yb
Y b 坐标松弛步(coordinate relaxation step) . 下图表示, 我们选取基矩阵
B
B
B
A
A
A
B
B
B
A
A
A
简单消元成本较低但可能会带来数值上的不稳定 . 若上图中的可行集为一条几近与
x
1
x_1
x 1
x
x
x
x
2
x_2
x 2
Y
b
Yb
Y b
为推广上一小节的内容, 我们选取
Y
∈
R
n
×
m
,
Z
∈
R
n
×
(
n
−
m
)
Y\in\mathbb{R}^{n\times m},Z\in\mathbb{R}^{n\times (n-m)}
Y ∈ R n × m , Z ∈ R n × ( n − m )
[
Y
∣
Z
]
∈
R
n
×
n
非
奇
异
,
A
Z
=
O
.
[Y\mid Z]\in\mathbb{R}^{n\times n}非奇异,\quad AZ=O.
[ Y ∣ Z ] ∈ R n × n 非 奇 异 , A Z = O .
Z
Z
Z
A
A
A
A
A
A
A
[
Y
∣
Z
]
=
[
A
Y
∣
O
]
A[Y\mid Z]=[AY\mid O]
A [ Y ∣ Z ] = [ A Y ∣ O ]
A
Y
AY
A Y
A
x
=
b
Ax=b
A x = b
x
=
Y
x
Y
+
Z
x
Z
,
x=Yx_Y+Zx_Z,
x = Y x Y + Z x Z ,
x
Y
∈
R
m
,
x
Z
∈
R
n
−
m
x_Y\in\mathbb{R}^m,x_Z\in\mathbb{R}^{n-m}
x Y ∈ R m , x Z ∈ R n − m
A
x
=
(
A
Y
)
x
Y
=
b
;
Ax=(AY)x_Y=b;
A x = ( A Y ) x Y = b ;
A
Y
AY
A Y
x
Y
x_Y
x Y
x
Y
=
(
A
Y
)
−
1
b
.
x_Y=(AY)^{-1}b.
x Y = ( A Y ) − 1 b .
x
x
x
x
Z
∈
R
n
−
m
x_Z\in\mathbb{R}^{n-m}
x Z ∈ R n − m
x
=
Y
(
A
Y
)
−
1
b
+
Z
x
Z
x=Y(AY)^{-1}b+Zx_Z
x = Y ( A Y ) − 1 b + Z x Z
A
x
=
b
Ax=b
A x = b
min
x
Z
f
(
Y
(
A
Y
)
−
1
b
+
Z
x
Z
)
.
\min_{x_Z}f(Y(AY)^{-1}b+Zx_Z).
x Z min f ( Y ( A Y ) − 1 b + Z x Z ) .
A
Y
AY
A Y
A
T
A^T
A T
Y
,
Z
Y,Z
Y , Z
A
T
Π
=
[
Q
1
Q
2
]
[
R
O
]
,
A^T\Pi=\begin{bmatrix}Q_1 & Q_2\end{bmatrix}\begin{bmatrix}R\\O\end{bmatrix},
A T Π = [ Q 1 Q 2 ] [ R O ] ,
[
Q
1
Q
2
]
\begin{bmatrix}Q_1&Q_2\end{bmatrix}
[ Q 1 Q 2 ]
Q
1
,
Q
2
Q_1,Q_2
Q 1 , Q 2
n
×
m
,
n
×
(
n
−
m
)
n\times m,n\times(n-m)
n × m , n × ( n − m )
R
R
R
m
×
m
m\times m
m × m
P
i
Pi
P i
m
×
m
m\times m
m × m
Y
=
Q
1
,
Z
=
Q
2
,
Y=Q_1,\quad Z=Q_2,
Y = Q 1 , Z = Q 2 ,
Y
,
Z
Y, Z
Y , Z
R
n
\mathbb{R}^n
R n
A
Y
=
Π
R
T
,
A
Z
=
O
.
AY=\Pi R^T,\quad AZ=O.
A Y = Π R T , A Z = O .
Y
,
Z
Y,Z
Y , Z 且
A
Y
AY
A Y
R
R
R , 从而与
A
A
A
A
x
=
b
Ax=b
A x = b
x
=
Q
1
R
−
T
Π
T
b
+
Q
2
x
Z
.
x=Q_1R^{-T}\Pi^Tb+Q_2x_Z.
x = Q 1 R − T Π T b + Q 2 x Z .
R
−
T
Π
T
b
R^{-T}\Pi^Tb
R − T Π T b
注意特解
Q
1
R
−
T
Π
T
b
Q_1R^{-T}\Pi^Tb
Q 1 R − T Π T b
A
T
(
A
A
T
)
−
1
b
A^T(AA^T)^{-1}b
A T ( A A T ) − 1 b
min
∥
x
∥
2
,
s
u
b
j
e
c
t
 
t
o
 
A
x
=
b
;
\min\Vert x\Vert^2,\quad\mathrm{subject\,to\,}Ax=b;
min ∥ x ∥ 2 , s u b j e c t t o A x = b ;
A
x
=
b
Ax=b
A x = b
使用正交基的消元法从数值稳定性上讲是理想的 . 而这一消元策略的主要计算量在于QR分解 . 不幸的是, 对于
A
A
A . 因此也有人提出其他的折中技术.
仍假设
P
=
I
P=I
P = I
Y
=
[
I
(
B
−
1
N
)
T
]
,
Z
=
[
−
B
−
1
N
I
]
.
Y=\begin{bmatrix}I\\(B^{-1}N)^T\end{bmatrix},\quad Z=\begin{bmatrix}-B^{-1}N\\I\end{bmatrix}.
Y = [ I ( B − 1 N ) T ] , Z = [ − B − 1 N I ] .
Y
,
Z
Y, Z
Y , Z
A
Z
=
O
,
Y
T
Z
=
O
AZ=O,Y^TZ=O
A Z = O , Y T Z = O
Y
,
Z
Y,Z
Y , Z
Y
(
A
Y
)
−
1
b
Y(AY)^{-1}b
Y ( A Y ) − 1 b
A
x
=
b
Ax=b
A x = b
Y
(
A
Y
)
−
1
=
[
I
(
B
−
1
N
)
T
]
(
B
+
N
N
T
B
−
T
)
−
1
=
[
I
(
B
−
1
N
)
T
]
(
A
A
T
B
−
T
)
−
1
=
[
B
T
N
T
]
(
A
A
T
)
−
1
=
A
(
A
A
T
)
−
1
.
\begin{aligned}Y(AY)^{-1}&=\begin{bmatrix}I\\(B^{-1}N)^T\end{bmatrix}(B+NN^TB^{-T})^{-1}\\&=\begin{bmatrix}I\\(B^{-1}N)^T\end{bmatrix}\left(AA^TB^{-T}\right)^{-1}\\&=\begin{bmatrix}B^T\\N^T\end{bmatrix}(AA^T)^{-1}=A(AA^T)^{-1}.\end{aligned}
Y ( A Y ) − 1 = [ I ( B − 1 N ) T ] ( B + N N T B − T ) − 1 = [ I ( B − 1 N ) T ] ( A A T B − T ) − 1 = [ B T N T ] ( A A T ) − 1 = A ( A A T ) − 1 .
Y
(
A
Y
)
−
1
Y(AY)^{-1}
Y ( A Y ) − 1
B
B
B 其条件数仅由
A
A
A . 不过仍要注意, 矩阵
Z
Z
Z
B
B
B
B
B
B
不等式约束存在时, 消元并不总能带来积极的效果 . 例如, 若例3中的问题再加上约束
x
≥
0
x\ge0
x ≥ 0
x
3
,
x
6
x_3,x_6
x 3 , x 6
(
x
1
,
x
2
,
x
4
,
x
5
)
≥
0
,
8
x
1
−
6
x
2
+
9
x
4
+
4
x
5
≤
6
,
(
3
/
4
)
x
1
+
(
1
/
2
)
x
2
−
(
1
/
4
)
x
4
+
(
3
/
2
)
x
5
≤
−
1.
\begin{aligned}(x_1,x_2,x_4,x_5)&\ge0,\\8x_1-6x_2+9x_4+4x_5&\le6,\\(3/4)x_1+(1/2)x_2-(1/4)x_4+(3/2)x_5&\le-1.\end{aligned}
( x 1 , x 2 , x 4 , x 5 ) 8 x 1 − 6 x 2 + 9 x 4 + 4 x 5 ( 3 / 4 ) x 1 + ( 1 / 2 ) x 2 − ( 1 / 4 ) x 4 + ( 3 / 2 ) x 5 ≥ 0 , ≤ 6 , ≤ − 1 .
但若给例3加上的是
3
x
1
+
2
x
3
≥
1
3x_1+2x_3\ge1
3 x 1 + 2 x 3 ≥ 1
−
13
x
1
+
12
x
2
−
18
x
4
−
8
x
5
≥
−
11.
-13x_1+12x_2-18x_4-8x_5\ge-11.
− 1 3 x 1 + 1 2 x 2 − 1 8 x 4 − 8 x 5 ≥ − 1 1 .
假设求解非线性规划问题的算法产生了一步减少了目标函数值但增加了约束的违反度. 我们应当接收这一步吗?
想要回答这个问题并不容易. 我们必须寻求一种权衡二者 的方法. 价值函数merit functions 法和滤子filters 法为达成平衡的两种方法. 在约束优化算法中, 一迭代步
p
p
p
ϕ
\phi
ϕ
在无约束优化里, 目标函数
f
f
f
f
f
f
在无约束优化的可行方法(即初始点和后续迭代点均满足问题约束)里, 目标函数仍然是价值函数的一种适宜选择;
在不可行方法(及允许迭代点违反约束)中, 我们需要评估迭代步和迭代点的质量, 此时的价值函数就要结合目标函数和约束的违反度 .
对于非线性规划问题的一类广受欢迎的价值函数是
l
1
l_1
l 1 罚函数 :
ϕ
1
(
x
;
μ
)
=
f
(
x
)
+
μ
∑
i
∈
E
∣
c
i
(
x
)
∣
+
μ
∑
i
∈
I
[
c
i
(
x
)
]
−
,
\phi_1(x;\mu)=f(x)+\mu\sum_{i\in\mathcal{E}}|c_i(x)|+\mu\sum_{i\in\mathcal{I}}[c_i(x)]^{-},
ϕ 1 ( x ; μ ) = f ( x ) + μ i ∈ E ∑ ∣ c i ( x ) ∣ + μ i ∈ I ∑ [ c i ( x ) ] − ,
[
z
]
−
=
max
{
0
,
−
z
}
[z]^{-}=\max\{0,-z\}
[ z ] − = max { 0 , − z }
μ
\mu
μ 惩罚因子(penalty parameter) , 它表现了我们给约束违反度所赋的权重. 注意
l
1
l_1
l 1
ϕ
1
\phi_1
ϕ 1
[
⋅
]
−
1
[\cdot]^{-1}
[ ⋅ ] − 1 精确(exact)的价值函数 .定义1 (Exact Merit Function ) 我们称价值函数
ϕ
(
x
;
μ
)
\phi(x;\mu)
ϕ ( x ; μ )
μ
∗
\mu^*
μ ∗
∀
μ
>
μ
∗
\forall\mu>\mu^*
∀ μ > μ ∗
ϕ
(
x
;
μ
)
\phi(x;\mu)
ϕ ( x ; μ )
l
1
l_1
l 1
ϕ
1
(
x
;
μ
)
\phi_1(x;\mu)
ϕ 1 ( x ; μ )
μ
∗
\mu^*
μ ∗
μ
∗
=
max
{
∣
λ
i
∗
∣
,
i
∈
E
∪
I
}
,
\mu^*=\max\{|\lambda_i^*|,i\in\mathcal{E}\cup\mathcal{I}\},
μ ∗ = max { ∣ λ i ∗ ∣ , i ∈ E ∪ I } ,
λ
i
∗
\lambda_i^*
λ i ∗
x
∗
x^*
x ∗
l
1
l_1
l 1 调整惩罚因子 的策略. 这些策略依赖于所选取的优化算法, 我们将在后面的章节里详细讨论.
另一种常用的价值函数是精确
l
2
l_2
l 2 , 它对不等式约束问题有形式
ϕ
2
(
x
;
μ
)
=
f
(
x
)
+
μ
∥
c
(
x
)
∥
2
.
\phi_2(x;\mu)=f(x)+\mu\Vert c(x)\Vert_2.
ϕ 2 ( x ; μ ) = f ( x ) + μ ∥ c ( x ) ∥ 2 .
2
−
2-
2 −
有一些函数既光滑又精确 . 为保证函数同时拥有两种性质, 我们必须在价值函数中增加额外的项. 对于等式约束问题, Fletcher增广Lagrange函数Fletcher’s augmented Lagrangian 为
ϕ
F
(
x
;
μ
)
=
f
(
x
)
−
λ
(
x
)
T
c
(
x
)
+
1
2
μ
∑
i
∈
E
c
i
(
x
)
2
,
\phi_F(x;\mu)=f(x)-\lambda(x)^Tc(x)+\frac{1}{2}\mu\sum_{i\in\mathcal{E}}c_i(x)^2,
ϕ F ( x ; μ ) = f ( x ) − λ ( x ) T c ( x ) + 2 1 μ i ∈ E ∑ c i ( x ) 2 ,
μ
>
0
\mu>0
μ > 0
λ
(
x
)
=
[
A
(
x
)
]
†
∇
f
(
x
)
=
[
A
(
x
)
A
(
x
)
T
]
−
1
A
(
x
)
∇
f
(
x
)
.
\lambda(x)=[A(x)]^{\dagger}\nabla f(x)=[A(x)A(x)^T]^{-1}A(x)\nabla f(x).
λ ( x ) = [ A ( x ) ] † ∇ f ( x ) = [ A ( x ) A ( x ) T ] − 1 A ( x ) ∇ f ( x ) .
A
(
x
)
A(x)
A ( x )
c
(
x
)
c(x)
c ( x )
λ
(
x
)
\lambda(x)
λ ( x )
λ
(
x
)
\lambda(x)
λ ( x )
一种稍微不同的价值函数为标准增广Lagrange函数 . 对不等式约束问题有形式
L
A
(
x
,
λ
;
μ
)
=
f
(
x
)
−
λ
T
c
(
x
)
+
1
2
μ
∥
c
(
x
)
∥
2
2
.
\mathcal{L}_A(x,\lambda;\mu)=f(x)-\lambda^Tc(x)+\frac{1}{2}\mu\Vert c(x)\Vert_2^2.
L A ( x , λ ; μ ) = f ( x ) − λ T c ( x ) + 2 1 μ ∥ c ( x ) ∥ 2 2 .
L
A
(
x
+
,
λ
+
;
μ
)
,
L
A
(
x
,
λ
;
μ
)
\mathcal{L}_A(x^+,\lambda^+;\mu),\mathcal{L}_A(x,\lambda;\mu)
L A ( x + , λ + ; μ ) , L A ( x , λ ; μ )
(
x
+
,
λ
+
)
(x^+,\lambda^+)
( x + , λ + )
L
A
\mathcal{L}_A
L A 非线性规划问题的解往往并不是
L
A
\mathcal{L}_A
L A . 尽管一些逐步二次规划算法通过自适应地调整
μ
,
λ
\mu,\lambda
μ , λ
L
A
\mathcal{L}_A
L A
ϕ
1
,
ϕ
2
\phi_1,\phi_2
ϕ 1 , ϕ 2
由线搜索得到的试探点
x
+
=
x
+
α
p
x^+=x+\alpha p
x + = x + α p
ϕ
(
x
;
μ
)
\phi(x;\mu)
ϕ ( x ; μ )
l
1
,
l
2
l_1,l_2
l 1 , l 2
ϕ
(
x
;
μ
)
\phi(x;\mu)
ϕ ( x ; μ )
p
p
p
D
(
ϕ
(
x
;
μ
)
;
p
)
.
D(\phi(x;\mu);p).
D ( ϕ ( x ; μ ) ; p ) .
线搜索算法中, 充分下降条件要求步长
α
>
0
\alpha>0
α > 0
ϕ
(
x
+
α
p
;
μ
)
≤
ϕ
(
x
;
μ
)
+
η
α
D
(
ϕ
(
x
;
μ
)
;
p
)
,
η
∈
(
0
,
1
)
.
\phi(x+\alpha p;\mu)\le\phi(x;\mu)+\eta\alpha D(\phi(x;\mu);p),\quad\eta\in(0,1).
ϕ ( x + α p ; μ ) ≤ ϕ ( x ; μ ) + η α D ( ϕ ( x ; μ ) ; p ) , η ∈ ( 0 , 1 ) .
ϕ
(
x
;
μ
)
−
ϕ
(
x
+
α
p
;
μ
)
\phi(x;\mu)-\phi(x+\alpha p;\mu)
ϕ ( x ; μ ) − ϕ ( x + α p ; μ )
−
α
D
(
ϕ
(
x
;
μ
)
;
p
)
-\alpha D(\phi(x;\mu);p)
− α D ( ϕ ( x ; μ ) ; p )
信赖域算法则一般使用一个二次模型
q
(
p
)
q(p)
q ( p )
ϕ
\phi
ϕ
ϕ
(
x
+
p
;
μ
)
≤
ϕ
(
x
;
μ
)
−
η
(
q
(
0
)
−
q
(
p
)
)
,
η
∈
(
0
,
1
)
.
\phi(x+p;\mu)\le\phi(x;\mu)-\eta(q(0)-q(p)),\quad\eta\in(0,1).
ϕ ( x + p ; μ ) ≤ ϕ ( x ; μ ) − η ( q ( 0 ) − q ( p ) ) , η ∈ ( 0 , 1 ) .
q
(
0
)
−
q
(
p
)
q(0)-q(p)
q ( 0 ) − q ( p )
滤子法是一种基于多目标优化 的迭代步接收机制. 我们知道非线性规划有两个目标: 极小化目标函数、满足约束. 若定义约束违反度为
h
(
x
)
∑
i
∈
E
∣
c
i
(
x
)
∣
+
∑
i
∈
I
[
c
i
(
x
)
]
−
1
,
h(x)\sum_{i\in\mathcal{E}}|c_i(x)|+\sum_{i\in\mathcal{I}}[c_i(x)]^{-1},
h ( x ) i ∈ E ∑ ∣ c i ( x ) ∣ + i ∈ I ∑ [ c i ( x ) ] − 1 ,
min
x
f
(
x
)
,
min
x
h
(
x
)
.
\min_xf(x),\quad\min_xh(x).
x min f ( x ) , x min h ( x ) . 以一定的权重合成为一个极小化问题 , 而滤子法则保持这两个目标是分离的. 若
(
f
(
x
+
)
,
h
(
x
+
)
)
(f(x^+),h(x^+))
( f ( x + ) , h ( x + ) )
(
f
l
,
h
l
)
=
(
f
(
x
l
)
,
h
(
x
l
)
)
(f_l,h_l)=(f(x_l),h(x_l))
( f l , h l ) = ( f ( x l ) , h ( x l ) )
x
+
x^+
x +
定义2
称二元组
(
f
k
,
h
k
)
(f_k,h_k)
( f k , h k ) 占优 二元组
(
f
l
,
h
l
)
(f_l,h_l)
( f l , h l )
f
k
≤
f
l
,
h
k
≤
h
l
f_k\le f_l,h_k\le h_l
f k ≤ f l , h k ≤ h l
滤子 是一些二元组
(
f
l
,
h
l
)
(f_l,h_l)
( f l , h l ) 称迭代点
x
k
x_k
x k 接收 , 若
(
f
k
,
h
k
)
(f_k,h_k)
( f k , h k )
当迭代点
x
k
x_k
x k
(
f
k
,
h
k
)
(f_k,h_k)
( f k , h k )
(
f
l
,
h
l
)
(f_l,h_l)
( f l , h l )
如图所示, 滤子中的每个元组都对应了一个无限长方形区域, 而这些区域的并就构成了当前滤子的不可接收域. 具体地说, 试探点
x
+
x^+
x +
(
f
+
,
h
+
)
(f^+,h^+)
( f + , h + ) 左下方 .
为比较滤子法和价值函数法, 我们在下图中用虚线画出使得
f
+
μ
h
=
f
k
+
μ
h
k
f+\mu h=f_k+\mu h_k
f + μ h = f k + μ h k
虚线左端的区域就是可降低价值函数
ϕ
(
x
;
μ
)
=
f
(
x
)
+
μ
h
(
x
)
\phi(x;\mu)=f(x)+\mu h(x)
ϕ ( x ; μ ) = f ( x ) + μ h ( x ) 一般一个试探点被滤子法所接收的可能性大于被价值函数法所接收的可能性 .
在滤子法中也有线搜索和信赖域. 若线搜索得到的试探点
x
+
=
x
k
+
α
k
p
k
x^+=x_k+\alpha_kp_k
x + = x k + α k p k
(
f
+
,
h
+
)
(f^+,h^+)
( f + , h + )
x
k
+
1
=
x
+
x_{k+1}=x^+
x k + 1 = x +
为使滤子法获得全局收敛 和较好的实用表现, 我们需对算法做许多强化.
首先, 我们需要保证算法不会接收特别接近当前
(
f
k
,
h
k
)
(f_k,h_k)
( f k , h k )
(
f
,
h
)
(f,h)
( f , h )
x
+
x^+
x +
(
f
j
,
h
j
)
(f_j,h_j)
( f j , h j )
f
(
x
+
)
≤
f
j
−
β
h
j
或
h
(
x
+
)
≤
h
j
−
β
h
j
,
f(x^+)\le f_j-\beta h_j\quad 或\quad h(x^+)\le h_j-\beta h_j,
f ( x + ) ≤ f j − β h j 或 h ( x + ) ≤ h j − β h j ,
β
∈
(
0
,
1
)
\beta\in(0,1)
β ∈ ( 0 , 1 )
β
=
1
0
−
5
\beta=10^{-5}
β = 1 0 − 5
f
(
x
+
)
≤
f
j
−
β
h
+
.
f(x^+)\le f_j-\beta h^+.
f ( x + ) ≤ f j − β h + .
第二个加强方面是要解决滤子法一些内在的问题. 在一定条件下, 由线搜索产生的搜索方向可能需要滤子能接收任意小的步长
α
k
\alpha_k
α k
α
min
\alpha_{\min}
α min 可行性恢复阶段(feasibility restoration phase) , 我们等会儿再介绍. 类似地, 在信赖域算法中, 若一串试探点被滤子连续地拒绝, 则信赖域半径可能会过小使得子问题变得不可行. 此时也要调用可行性恢复阶段. 当然我们也可以使用其他的手段, 但我们下面会说到, 可行性恢复阶段对算法还有他用.
可行性恢复阶段专门用于减小约束违反度 . 即要求得以下问题的近似解:
min
x
h
(
x
)
.
\min_xh(x).
x min h ( x ) .
h
(
x
)
h(x)
h ( x )
h
h
h
下面我们给出信赖域算法下滤子法的框架. 在之后的章节中我们会讨论约束优化的信赖域算法.
算法1 (General Filter Method)
x
0
x_0
x 0
Δ
0
\Delta_0
Δ 0
k
←
0
k\leftarrow0
k ← 0
\quad\quad
\quad\quad\quad\quad
x
k
+
1
x_{k+1}
x k + 1
\quad\quad
\quad\quad\quad\quad
x
+
=
x
k
+
p
k
x^+=x_k+p_k
x + = x k + p k
\quad\quad\quad\quad
(
f
+
,
h
+
)
(f^+,h^+)
( f + , h + )
\quad\quad\quad\quad\quad\quad
x
k
+
1
=
x
+
x_{k+1}=x^+
x k + 1 = x +
(
f
k
+
1
,
h
k
+
1
)
(f_{k+1},h_{k+1})
( f k + 1 , h k + 1 )
\quad\quad\quad\quad\quad\quad
Δ
k
+
1
\Delta_{k+1}
Δ k + 1
Δ
k
+
1
≥
Δ
k
\Delta_{k+1}\ge\Delta_k
Δ k + 1 ≥ Δ k
\quad\quad\quad\quad\quad\quad
(
f
k
+
1
,
h
k
+
1
)
(f_{k+1},h_{k+1})
( f k + 1 , h k + 1 )
\quad\quad\quad\quad
\quad\quad\quad\quad\quad\quad
x
k
+
1
=
x
k
x_{k+1}=x_k
x k + 1 = x k
\quad\quad\quad\quad\quad\quad
Δ
k
+
1
<
Δ
k
\Delta_{k+1}<\Delta_k
Δ k + 1 < Δ k
\quad\quad\quad\quad
\quad\quad
\quad\quad
k
←
k
+
1
k\leftarrow k+1
k ← k + 1
其他的加强措施则依赖于之后章节中的具体算法.
基于价值函数或滤子的一些算法可能无法快速收敛, 是因为它们拒绝了好的试探点 . 这种现象被称为Maratos效应(Maratos effect) , 这由Maratos首次发现. Maratos效应可用下面的例子阐明, 其中本可以带来二次收敛的
p
k
p_k
p k
例4 考虑问题
min
f
(
x
1
,
x
2
)
=
2
(
x
1
2
+
x
2
2
−
1
)
−
x
1
,
s
u
b
j
e
c
t
 
t
o
 
x
1
2
+
x
2
2
−
1
=
0.
\min f(x_1,x_2)=2(x_1^2+x_2^2-1)-x_1,\quad\mathrm{subject\,to\,}x_1^2+x_2^2-1=0.
min f ( x 1 , x 2 ) = 2 ( x 1 2 + x 2 2 − 1 ) − x 1 , s u b j e c t t o x 1 2 + x 2 2 − 1 = 0 .
可以验证最优解为
x
∗
=
(
1
,
0
)
T
x^*=(1,0)^T
x ∗ = ( 1 , 0 ) T
λ
∗
=
3
2
\lambda^*=\frac{3}{2}
λ ∗ = 2 3
∇
x
x
2
L
(
x
∗
,
λ
∗
)
=
I
\nabla^2_{xx}\mathcal{L}(x^*,\lambda^*)=I
∇ x x 2 L ( x ∗ , λ ∗ ) = I
考虑迭代点
x
k
=
(
cos
θ
,
sin
θ
)
T
x_k=(\cos\theta,\sin\theta)^T
x k = ( cos θ , sin θ ) T
θ
\theta
θ
p
k
=
[
sin
2
θ
−
sin
θ
cos
θ
]
,
p_k=\begin{bmatrix}\sin^2\theta\\-\sin\theta\cos\theta\end{bmatrix},
p k = [ sin 2 θ − sin θ cos θ ] ,
x
k
+
p
k
=
[
cos
θ
+
sin
2
θ
sin
θ
(
1
−
cos
θ
)
]
.
x_k+p_k=\begin{bmatrix}\cos\theta+\sin^2\theta\\\sin\theta(1-\cos\theta)\end{bmatrix}.
x k + p k = [ cos θ + sin 2 θ sin θ ( 1 − cos θ ) ] .
∥
x
k
+
p
k
−
x
∗
∥
2
=
2
sin
2
(
θ
/
2
)
,
∥
x
k
−
x
∗
∥
2
=
2
∣
sin
(
θ
/
2
)
∣
,
\Vert x_k+p_k-x^*\Vert_2=2\sin^2(\theta/2),\quad\Vert x_k-x^*\Vert_2=2|\sin(\theta/2)|,
∥ x k + p k − x ∗ ∥ 2 = 2 sin 2 ( θ / 2 ) , ∥ x k − x ∗ ∥ 2 = 2 ∣ sin ( θ / 2 ) ∣ ,
∥
x
k
+
p
k
−
x
∗
∥
2
∥
x
k
−
x
∗
∥
2
2
=
1
2
.
\frac{\Vert x_k+p_k-x^*\Vert_2}{\Vert x_k-x^*\Vert_2^2}=\frac{1}{2}.
∥ x k − x ∗ ∥ 2 2 ∥ x k + p k − x ∗ ∥ 2 = 2 1 .
f
(
x
k
+
p
k
)
=
sin
2
θ
−
cos
θ
>
−
cos
θ
=
f
(
x
k
)
,
c
(
x
k
+
p
k
)
=
sin
2
θ
>
0
=
c
(
x
k
)
,
\begin{aligned}f(x_k+p_k)&=\sin^2\theta-\cos\theta>-\cos\theta=f(x_k),\\c(x_k+p_k)&=\sin^2\theta>0=c(x_k),\end{aligned}
f ( x k + p k ) c ( x k + p k ) = sin 2 θ − cos θ > − cos θ = f ( x k ) , = sin 2 θ > 0 = c ( x k ) ,
θ
≠
0
\theta\ne0
θ ̸ = 0
对于以上例子, 任何基于具有形式
ϕ
(
x
;
μ
)
=
f
(
x
)
+
μ
h
(
c
(
x
)
)
\phi(x;\mu)=f(x)+\mu h(c(x))
ϕ ( x ; μ ) = f ( x ) + μ h ( c ( x ) )
h
(
⋅
)
h(\cdot)
h ( ⋅ )
h
(
0
)
=
0
h(0)=0
h ( 0 ) = 0
如果不采取补救措施, Maratos效应就可能会影响优化算法的收敛速度 . 避免Maratos效应的策略包括以下:
我们可以使用不会被Maratos效应影响的价值函数. 例如Fletcher增广Lagrange函数.
使用二阶校正步(second-order correction step) : 在
c
(
x
k
+
p
k
)
c(x_k+p_k)
c ( x k + p k )
p
^
k
\hat{p}_k
p ^ k
p
k
p_k
p k
p
^
k
\hat{p}_k
p ^ k
允许价值函数
ϕ
\phi
ϕ 非单调策略(nonmonotone strategy) .
我们在下一节讨论后面两种方法.
通过增加校正项减小约束违反度, 许多算法就能够克服Maratos效应. 我们以等式约束为例介绍这一技术.
给定
p
k
p_k
p k 二阶校正步(the second-order correction step)
p
^
k
\hat{p}_k
p ^ k
p
^
k
=
−
A
k
T
(
A
k
A
k
T
)
−
1
c
(
x
k
+
p
k
)
,
\hat{p}_k=-A_k^T(A_kA_k^T)^{-1}c(x_k+p_k),
p ^ k = − A k T ( A k A k T ) − 1 c ( x k + p k ) ,
A
k
=
A
(
x
k
)
A_k=A(x_k)
A k = A ( x k )
c
c
c
x
k
x_k
x k
p
^
k
\hat{p}_k
p ^ k
c
c
c
x
k
+
p
k
x_k+p_k
x k + p k
A
k
p
^
k
+
c
(
x
k
+
p
k
)
=
0.
A_k\hat{p}_k+c(x_k+p_k)=0.
A k p ^ k + c ( x k + p k ) = 0 .
p
^
k
\hat{p}_k
p ^ k
p
^
k
\hat{p}_k
p ^ k
在
p
k
p_k
p k
A
k
p
k
+
c
(
x
k
)
=
0
A_kp_k+c(x_k)=0
A k p k + c ( x k ) = 0
p
^
k
\hat{p}_k
p ^ k
∥
c
(
x
)
∥
\Vert c(x)\Vert
∥ c ( x ) ∥
∥
x
k
−
x
∗
∥
3
\Vert x_k-x^*\Vert^3
∥ x k − x ∗ ∥ 3
x
k
x_k
x k
x
k
+
p
k
+
p
^
k
x_k+p_k+\hat{p}_k
x k + p k + p ^ k
c
c
c
x
k
+
p
k
x_k+p_k
x k + p k
p
^
k
\hat{p}_k
p ^ k
下面给出在线搜索中使用价值函数和二阶校正步的算法. 假设搜索方向
p
k
p_k
p k
μ
k
\mu_k
μ k
p
k
p_k
p k
D
(
ϕ
(
x
k
;
μ
)
;
p
k
)
<
0
D(\phi(x_k;\mu);p_k)<0
D ( ϕ ( x k ; μ ) ; p k ) < 0
这一算法的关键特征是, 若满步
α
k
=
1
\alpha_k=1
α k = 1 算法在沿着原始方向
p
k
p_k
p k .
算法2 (Generic Algorithm with Second-Order Correction)
η
∈
(
0
,
0.5
)
\eta\in(0,0.5)
η ∈ ( 0 , 0 . 5 )
τ
1
,
τ
2
:
0
<
τ
1
<
τ
2
<
1
\tau_1,\tau_2:0<\tau_1<\tau_2<1
τ 1 , τ 2 : 0 < τ 1 < τ 2 < 1
x
0
x_0
x 0
k
←
0
k\leftarrow0
k ← 0
\quad\quad
p
k
p_k
p k
\quad\quad
α
k
←
1
\alpha_k\leftarrow1
α k ← 1
←
\leftarrow
←
\quad\quad
\quad\quad\quad\quad
ϕ
(
x
k
+
α
k
p
k
;
μ
)
≤
ϕ
(
x
k
;
μ
)
+
η
α
k
D
(
ϕ
(
x
k
;
μ
)
;
p
k
)
\phi(x_k+\alpha_kp_k;\mu)\le\phi(x_k;\mu)+\eta\alpha_kD(\phi(x_k;\mu);p_k)
ϕ ( x k + α k p k ; μ ) ≤ ϕ ( x k ; μ ) + η α k D ( ϕ ( x k ; μ ) ; p k )
\quad\quad\quad\quad\quad\quad
x
k
+
1
←
x
k
+
α
k
p
k
x_{k+1}\leftarrow x_k+\alpha_kp_k
x k + 1 ← x k + α k p k
\quad\quad\quad\quad\quad\quad
←
\leftarrow
←
\quad\quad\quad\quad
α
k
=
1
\alpha_k=1
α k = 1
\quad\quad\quad\quad\quad\quad
p
^
k
\hat{p}_k
p ^ k
\quad\quad\quad\quad\quad\quad
ϕ
(
x
k
+
p
k
+
p
^
k
;
μ
)
≤
ϕ
(
x
k
;
μ
)
+
η
D
(
ϕ
(
x
k
;
μ
)
;
p
k
)
\phi(x_k+p_k+\hat{p}_k;\mu)\le\phi(x_k;\mu)+\eta D(\phi(x_k;\mu);p_k)
ϕ ( x k + p k + p ^ k ; μ ) ≤ ϕ ( x k ; μ ) + η D ( ϕ ( x k ; μ ) ; p k )
\quad\quad\quad\quad\quad\quad\quad\quad
x
k
+
1
←
x
k
+
p
k
+
p
^
k
x_{k+1}\leftarrow x_k+p_k+\hat{p}_k
x k + 1 ← x k + p k + p ^ k
\quad\quad\quad\quad\quad\quad\quad\quad
←
\leftarrow
←
\quad\quad\quad\quad\quad\quad
\quad\quad\quad\quad\quad\quad\quad\quad
α
k
\alpha_k
α k
[
τ
1
α
k
,
τ
2
α
k
]
[\tau_1\alpha_k,\tau_2\alpha_k]
[ τ 1 α k , τ 2 α k ]
\quad\quad\quad\quad\quad\quad
\quad\quad\quad\quad
\quad\quad\quad\quad\quad\quad
α
k
\alpha_k
α k
[
τ
1
α
k
,
τ
2
α
k
]
[\tau_1\alpha_k,\tau_2\alpha_k]
[ τ 1 α k , τ 2 α k ]
\quad\quad\quad\quad
\quad\quad
在上述算法中, 若
p
^
k
\hat{p}_k
p ^ k
p
k
+
p
^
k
p_k+\hat{p}_k
p k + p ^ k
二阶校正策略在实际中很高效. 它带来了强健性和效率. 因此额外的计算成本是值得的.
由Maratos效应带来的不便可通过偶尔接受增加价值函数的试探点避免. 这样的迭代步称作松弛步(relaxed steps) . 不过接受是有一定限度的. 如果接连几次(例如
t
^
\hat{t}
t ^
二阶校正仅改进约束的满意度 , 而非单调策略则意在同时改善可行性与最优性 . 我们希望价值函数的增加只是暂时的, 后续的迭代会得到极大的改良.
下面介绍一种非单调方法的特殊形式, 称作是watchdog策略 . 置
t
^
=
1
\hat{t}=1
t ^ = 1
ϕ
\phi
ϕ
μ
\mu
μ
ϕ
\phi
ϕ
μ
\mu
μ
ϕ
(
x
)
,
D
(
ϕ
(
x
)
;
p
k
)
\phi(x),D(\phi(x);p_k)
ϕ ( x ) , D ( ϕ ( x ) ; p k )
算法3 (Watchdog)
η
∈
(
0
,
0.5
)
\eta\in(0,0.5)
η ∈ ( 0 , 0 . 5 )
x
0
x_0
x 0
k
←
0
,
S
←
{
0
}
k\leftarrow0,\mathcal{S}\leftarrow\{0\}
k ← 0 , S ← { 0 }
\quad\quad
p
k
p_k
p k
\quad\quad
x
k
+
1
←
x
k
+
p
k
x_{k+1}\leftarrow x_k+p_k
x k + 1 ← x k + p k
\quad\quad
ϕ
(
x
k
+
1
)
≤
ϕ
(
x
k
)
+
η
D
(
ϕ
(
x
k
)
;
p
k
)
\phi(x_{k+1})\le\phi(x_k)+\eta D(\phi(x_k);p_k)
ϕ ( x k + 1 ) ≤ ϕ ( x k ) + η D ( ϕ ( x k ) ; p k )
\quad\quad\quad\quad
k
←
k
+
1
,
S
←
S
∪
{
k
}
k\leftarrow k+1,\mathcal{S}\leftarrow\mathcal{S}\cup\{k\}
k ← k + 1 , S ← S ∪ { k }
\quad\quad
\quad\quad\quad\quad
p
k
+
1
p_{k+1}
p k + 1
x
k
+
1
x_{k+1}
x k + 1
\quad\quad\quad\quad
α
k
+
1
\alpha_{k+1}
α k + 1
\quad\quad\quad\quad\quad\quad
ϕ
(
x
k
+
2
)
≤
ϕ
(
x
k
+
1
)
+
η
α
k
+
1
D
(
ϕ
(
x
k
+
1
)
;
p
k
+
1
)
\phi(x_{k+2})\le\phi(x_{k+1})+\eta\alpha_{k+1}D(\phi(x_{k+1});p_{k+1})
ϕ ( x k + 2 ) ≤ ϕ ( x k + 1 ) + η α k + 1 D ( ϕ ( x k + 1 ) ; p k + 1 )
\quad\quad\quad\quad
x
k
+
2
←
x
k
+
1
+
α
k
+
1
p
k
+
1
x_{k+2}\leftarrow x_{k+1}+\alpha_{k+1}p_{k+1}
x k + 2 ← x k + 1 + α k + 1 p k + 1
\quad\quad\quad\quad
ϕ
(
x
k
+
1
)
≤
ϕ
(
x
k
)
\phi(x_{k+1})\le\phi(x_k)
ϕ ( x k + 1 ) ≤ ϕ ( x k )
ϕ
(
x
k
+
1
)
≤
ϕ
(
x
k
)
+
η
D
(
ϕ
(
x
k
)
;
p
k
)
\phi(x_{k+1})\le\phi(x_k)+\eta D(\phi(x_k);p_k)
ϕ ( x k + 1 ) ≤ ϕ ( x k ) + η D ( ϕ ( x k ) ; p k )
\quad\quad\quad\quad
k
←
k
+
2
,
S
←
S
∪
{
k
}
k\leftarrow k+2,\mathcal{S}\leftarrow\mathcal{S}\cup\{k\}
k ← k + 2 , S ← S ∪ { k }
\quad\quad\quad\quad
ϕ
(
x
k
+
2
)
>
ϕ
(
x
k
)
\phi(x_{k+2})>\phi(x_k)
ϕ ( x k + 2 ) > ϕ ( x k )
\quad\quad\quad\quad\quad\quad
return to
x
k
x_k
x k
p
k
p_k
p k )
\quad\quad\quad\quad\quad\quad
α
k
\alpha_k
α k
ϕ
(
x
k
+
3
)
≤
ϕ
(
x
k
)
+
η
α
k
D
(
ϕ
(
x
k
)
;
p
k
)
\phi(x_{k+3})\le\phi(x_k)+\eta\alpha_kD(\phi(x_k);p_k)
ϕ ( x k + 3 ) ≤ ϕ ( x k ) + η α k D ( ϕ ( x k ) ; p k )
\quad\quad\quad\quad\quad\quad
x
k
+
3
=
x
k
+
α
k
p
k
x_{k+3}=x_k+\alpha_kp_k
x k + 3 = x k + α k p k
\quad\quad\quad\quad\quad\quad
k
←
k
+
3
,
S
←
S
∪
{
k
}
k\leftarrow k+3,\mathcal{S}\leftarrow\mathcal{S}\cup\{k\}
k ← k + 3 , S ← S ∪ { k }
\quad\quad\quad\quad
\quad\quad\quad\quad\quad\quad
p
k
+
2
p_{k+2}
p k + 2
x
k
+
2
x_{k+2}
x k + 2
\quad\quad\quad\quad\quad\quad
α
k
+
2
\alpha_{k+2}
α k + 2
\quad\quad\quad\quad\quad\quad\quad\quad
ϕ
(
x
k
+
3
)
≤
ϕ
(
x
k
+
2
)
+
η
α
k
+
2
D
(
ϕ
(
x
k
+
2
)
;
p
k
+
2
)
;
\phi(x_{k+3})\le\phi(x_{k+2})+\eta\alpha_{k+2}D(\phi(x_{k+2});p_{k+2});
ϕ ( x k + 3 ) ≤ ϕ ( x k + 2 ) + η α k + 2 D ( ϕ ( x k + 2 ) ; p k + 2 ) ;
\quad\quad\quad\quad\quad\quad
x
k
+
3
←
x
k
+
2
+
α
k
+
2
p
k
+
2
x_{k+3}\leftarrow x_{k+2}+\alpha_{k+2}p_{k+2}
x k + 3 ← x k + 2 + α k + 2 p k + 2
\quad\quad\quad\quad\quad\quad
k
←
k
+
3
,
S
←
S
∪
{
k
}
k\leftarrow k+3,\mathcal{S}\leftarrow\mathcal{S}\cup\{k\}
k ← k + 3 , S ← S ∪ { k }
\quad\quad\quad\quad
\quad\quad
其中集合
S
\mathcal{S}
S
S
\mathcal{S}
S 可以证明许多使用watchdog技术的约束优化算法是全局收敛的 . 我们也可以证明, 对于充分大的
k
k
k
α
k
=
1
\alpha_k=1
α k = 1 收敛速度超线性 .
实际中, 允许
t
^
>
1
\hat{t}>1
t ^ > 1
t
^
\hat{t}
t ^ 潜在的优势 是, 它可能需要计算更少的约束函数值 . 最好情形下, 所有迭代步均是满步, 且基本不需要再返回到之前的迭代点.