Numerical Optimization Ch13. Linear Programming: The Simplex Method

第十三章: 线性规划之单纯形法

Dantzig在上世纪四十年代末期发展的 单纯形法simplex method标志着优化领域进入了新的时代. 这一方法使得经济学家能够建立大型的模型并系统高效地分析它们. 更巧的是, Dantzig提出单纯形法的同时期恰逢第一台电子计算机的诞生, 从而单纯形法就成了这一新兴科技最早的应用之一. 自那时至今, 单纯形法的计算机实现不断为人完善. 这要部分归功于与数值分析的结合.
如今, 线性规划及单纯形法依然支配着优化领域. 自上世纪五十年代, 数代管理、经济、金融和工程界的工作者都要学会构建线性模型并使用基于单纯形法的软件求解问题. 通常, 他们碰到的模型实际上都是非线性的, 但 线性规划仍然有用. 原因有三:

• 单纯形法能保证收敛到全局极小点
• 单纯形法的软件工具的先进性
• 线性模型要比复杂的非线性模型稳定得多

随着非线性规划的软件的更新, 以及一类称为内点法的算法(现已证明, 内点法在某些线性规划问题中具有更快的收敛速度)的提出, 非线性规划在某些应用中可能会取代线性规划. 但在未来, 单纯形法的重要性一定会延续下去. 这是毋庸置疑的.

0. 线性规划简介

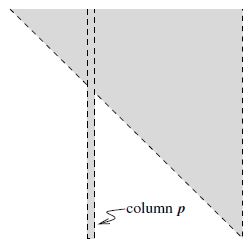
线性规划问题包括一个线性目标函数和有限个线性约束, 这些约束可能是等式约束, 也可能是不等式约束. 可以想见,

• 可行集是一个凸的、连通的多面体, 其面为多边形.
• 目标函数的等高线是平行的.

下图就刻画了一个二维线性规划问题, 其中目标函数的等高线以虚线表示.

此例的解唯一——可行集的一个顶点. 可以预见, 稍微改变一下约束或者目标函数就会使得解不再唯一. 此时 $c^Tx$在整条边上具有相同的值. 在更高维的情形下, 最优点集可能是单一顶点、一条边、一个面或者是整个可行集. 若可行集为空, 则称问题无解(infeasible case); 若目标函数在可行域中下无界, 则称问题无界(unbounded case).

线性规划问题通常以下面的标准形式出现和分析: $\min c^Tx,\quad\mathrm{subject\,to\,}Ax=b,x\ge0,$其中 $c,x\in\mathbb{R}^n,b\in\mathbb{R}^m,A\in\mathbb{R}^{m\times n}$. 事实上, 任意其他形式的线性规划问题都能转化成标准形式. 例如问题是 $\min c^Tx,\quad\mathrm{subject\,to\,}Ax\le b,$我们便可通过引入松弛变量(slack variables) $z$将不等式转换成等式: $\min c^Tx,\quad\mathrm{subject\,to\,}Ax+z=b,z\ge0.$这样还不是最标准的, 因为并不是所有的变量都有非负的约束. 对此, 我们将 $x$分成正部和负部: $x=x^+-x^-$, 其中 $x^+=\max(x,0)\ge0,x^-=\max(-x,0)\ge0$. 这样就有标准形式: $\min\begin{bmatrix}c\\-c\\0\end{bmatrix}^T\begin{bmatrix}x^+\\x^-\\z\end{bmatrix},\quad\mathrm{s.t.\,}\begin{bmatrix}A & -A & I\end{bmatrix}\begin{bmatrix}x^+\\x^-\\z\end{bmatrix}=b,\begin{bmatrix}x^+\\x^-\\z\end{bmatrix}\ge0.$事实上, 如 $x\le u$或者 $Ax\ge b$这样的约束都能用加或减松弛变量变成等式约束: $\begin{aligned}x\le u&\Leftrightarrow x+w=u,w\ge0,\\Ax\ge b&\Leftrightarrow Ax-y=b,y\ge0.\end{aligned}$第二种情形中, 有时我们也称 $y$为剩余变量(surplus variables). 另外, 我们可给目标函数添加负号将极大问题变成极小问题.

许多线性规划问题来自转运和分配网络的模型. 这些问题在它们的约束中具有额外的特殊结构, 因此充分考虑此信息的单纯形法会更加高效. 对此我们不深究, 我们只需要知道这种问题很重要也很复杂.

对于标准形式, 我们假设约束的个数小于变量的个数, 即 $m<n$. 否则, $Ax=b$必包含冗余的行或不可行, 或只定义了唯一点. 事实上当 $m\ge n$时, 我们可以用例如QR分解或LU分解的分解法将 $Ax=b$转换为系数矩阵行满秩的线性系统.

1. 最优性条件与对偶

1.1 最优性条件

线性规划问题的最优性条件可用第十二章的理论得到. 不过, 我们仅需一阶条件(KKT条件). 这是因为问题的凸性保证了KKT条件的充分性. 因而我们无需再诉诸二阶条件. (事实上二阶求导后Hessian阵是零.)

我们在第十二章中介绍的理论使线性规划的最优性和对偶结果的推导比其他情形更容易, 而在那些情形中, 这些理论或多或少是从零开始发展的.

KKT条件可由第十二章的定理1得到. 注意这个定理需要LICQ条件. 但在上一章的第六节我们提到, 只要积极约束均是线性的, 仍然有 $T_{\Omega}(x^*)=\mathcal{F}(x^*)$.

我们将Lagrange乘子分成两部分 $\lambda,s$, 其中 $\lambda\in\mathbb{R}^m$为等式约束 $Ax=b$对应的乘子向量(multiplier vector), $s\in\mathbb{R}^n$则是非负约束 $x\ge0$对应的乘子向量. 这样Lagrange函数就是 $\mathcal{L}(x,\lambda,s)=c^Tx-\lambda^T(Ax-b)-s^Tx.$由KKT条件, $x^*$为解的必要(且充分)条件为存在向量 $\lambda,s$使得: $\begin{aligned}A^T\lambda+s&=c,\\Ax&=b,\\x&\ge0,\\s&\ge0,\\x_is_i&=0,\quad i=1,2,\ldots,n.\end{aligned}$互补松弛条件表明对 $i=1,2,\ldots,n$, $x_i,s_i$二者至少有一个是0. 由于非负性的条件, 我们可将互补松弛条件等价地写作 $x^Ts=0$.

令 $(x^*,\lambda^*,s^*)$为满足KKT条件的三元组. 于是有 $c^Tx^*=(A^T\lambda^*+s^*)^Tx^*=(Ax^*)^T\lambda^*=b^T\lambda^*.$注意到 $b^T\lambda$正是线性规划对偶问题的目标函数, 因此上式表明对于满足KKT条件的三元组 $(x,\lambda,s)$, 原始目标和对偶目标是相等的. 事实上这在上一章的定理13中, 对于凸的 $f,-c_i$已有保障.

上述KKT条件易验证也是 $x^*$为全局解的充分条件. 令 $\bar{x}$为另一可行点, 使得 $A\bar{x}=b,\bar{x}\ge0$. 于是 $c^T\bar{x}=(A\lambda^*+s^*)^T\bar{x}=b^T\lambda^*+\bar{x}^Ts^*\ge b^T\lambda^*=c^Tx^*.$我们可以进一步得到, 可行点 $\bar{x}$为最优当且仅当 $\bar{x}^Ts^*=0,$否则上一个不等式就是严格成立的. 换句话说, 当 $s_i^*>0$, 对于所有的最优解 $\bar{x}$, 我们必有 $\bar{x}_i=0$.

1.2 对偶问题

给定 $c,b, A$, 我们可用上一章的方法定义相应的对偶问题. 将等式约束 $Ax=b$化为等价的 $Ax\ge b,b\ge Ax,$将原本的 $\lambda\in\mathbb{R}^m$换为 $0\le\lambda_1,\lambda_2\in\mathbb{R}^m$. $s$不变. 于是有对偶目标函数 $\begin{aligned}q(\lambda_1,\lambda_2,s)&=\inf_x\mathcal{L}(x,\lambda_1,\lambda_2,s)\\&=\inf_x c^Tx-\lambda_1^T(Ax-b)-\lambda_2^T(b-Ax)-s^Tx\\&=(c-A^T\lambda_1+A^T\lambda_2-s)^Tx+b^T(\lambda_1-\lambda_2).\end{aligned}$因此 $q(\lambda_1,\lambda_2,s)$有限仅当 $A^T(\lambda_1-\lambda_2)=c-s.$于是相应的对偶问题为 $\begin{array}{ll}\max_{\lambda_1,\lambda_2,s} & b^T(\lambda_1-\lambda_2)\\\mathrm{subject\,to\,} & A^T(\lambda_1-\lambda_2)=c-s,\\ & \lambda_1,\lambda_2,s\ge0.\end{array}$等价地, $\max_{\lambda}b^T\lambda,\quad\mathrm{subject\,to\,}A^T\lambda+s= c,\quad s\ge0.$变量对 $(\lambda,s)$有时被一起称作对偶变量(dual variables).

原始和对偶问题在同样的数据上给出了两种不同的观点. 当我们写出对偶问题的KKT条件时, 它们二者的联系会变得更加明显. 我们将对偶问题重述为以下形式 $\min -b^T\lambda\quad\mathrm{subject\,to\,}c-A^T\lambda\ge0.$令 $x\in\mathbb{R}^n$表示对应于 $A^T\lambda\le c$的Lagrange乘子, 我们有Lagrange函数 $\bar{\mathcal{L}}(\lambda,x)=-b^T\lambda-x^T(c-A^T\lambda).$由KKT条件, 我们得到 $\lambda$为对偶问题解的必要(且充分)条件是存在 $x$使得 $\begin{aligned}Ax&=b,\\A^T\lambda&\le c,\\x&\ge0,\\x_i(c-A^T\lambda)_i&=0,\quad i=1,2,\ldots,n.\end{aligned}$定义 $s=c-A^T\lambda$, 会发现原始问题和对偶问题的KKT条件是完全一样的. 具体说来,

• 原始问题的最优Lagrange乘子 $\lambda$成了对偶问题的最优变量
• 对偶问题的最优Lagrange乘子 $x$成了原始问题的最优变量.

同原始问题一样, 我们也可以证明上述条件是充分的. 给定 $x^*,\lambda^*$满足以上(从而三元组 $(x,\lambda,s)=(x^*,\lambda^*,c-A^T\lambda^*)$满足原始问题的KKT条件), 对于任意其他的对偶可行点 $\bar{\lambda}$(即 $A^T\bar{\lambda}\le c$), 我们有 $\begin{aligned}b^T\bar{\lambda}&=(x^*)^TA^T\bar{\lambda}\\&=(x^*)^T(A^T\bar{\lambda}-c)+c^Tx^*\\&\le c^Tx^*=b^T\lambda^*.\end{aligned}$易知这原始-对偶的关系是对称的, 即取上述对偶问题的对偶, 我们就得到了原来的原始问题.

由上一章的弱对偶原理, 给定原始问题的可行 $x$和对偶问题的可行对 $(\lambda,s)$, 我们有 $c^Tx\ge b^T\lambda.$下面我们给出线性规划的强对偶原理. 它是线性规划理论的基石.

定理1 (强对偶, strong duality)

1. 若原始或对偶问题二者有一个有有限解, 则另一个也是, 且解处二者的目标函数值相等.
2. 若二者有一个无界, 则另一个必不可行(无解).

证明: 对于第一条, 假设原始问题有有限最优解 $x^*$. 则从一阶最优性条件知存在 $\lambda^*,s^*$使得 $(x^*,\lambda^*,s^*)$满足KKT条件. 上面我们说到原始问题和对偶问题的KKT条件是等价的, 且对偶问题的KKT条件也是 $\lambda^*$为对偶问题解的充分条件. 进一步地, $c^Tx^*=b^T\lambda^*$.
相反方向的证明则由对称性得到.

为证明第二条, 先假设原始问题无界, 于是存在一列 $x^k,k=1,2,3,\ldots$使得 $c^Tx^k\downarrow-\infty,\quad Ax^k=b,\quad x^k\ge0.$若不然, 对偶问题可行, 则存在 $\bar{\lambda}$使得 $A^T\bar{\lambda}\le c$. 因此由弱对偶原理, 结合 $x^k$的非负性, 我们有 $\bar{\lambda}^Tb=\bar{\lambda}^TAx^k\le c^Tx^k\downarrow-\infty,$矛盾! 因此, 对偶问题必定无解. 反之, 可用对称性证明.

与上一章同, 乘子 $\lambda, s$的值反映了最优目标值对于约束扰动的敏感度. 事实上, 对于给定最优 $x$, 求得 $(\lambda,s)$的过程通常称作灵敏度分析(sensitivity analysis).
考虑对于向量 $b$(原始问题的右端项, 或对偶问题目标的梯度)的扰动, 我们现在做一些粗略的讨论. 假设这一扰动给原始和对偶解带来了微小了改变, 且改变量 $\Delta s,\Delta x$与 $s,x$具有相同的0. 因此, 由互补松弛条件, $0=x^Ts=x^T\Delta s=(\Delta x)^Ts=(\Delta x)^T\Delta s.$从强对偶定理, 我们知道扰动前后, 原始问题和对偶问题最优目标值都是相等的, 于是 $c^Tx=b^T\lambda,\quad c^T(x+\Delta x)=(b+\Delta b)^T(\lambda+\Delta\lambda).$进一步, 由扰动后解的可行性, 有 $A(x+\Delta x)=b+\Delta b,\quad A^T\Delta\lambda=-\Delta s.$因此, 原始问题最优目标值的改变量为 $\begin{aligned}c^T\Delta x&=(b+\Delta b)^T(\lambda+\Delta\lambda)-b^T\lambda\\&=(b+\Delta b)^T\Delta\lambda+(\Delta b)^T\lambda\\&=(x+\Delta x)^TA^T\Delta\lambda+(\Delta b)^T\lambda\\&=-(x+\Delta x)^T\Delta s+(\Delta b)^T\lambda\\&=(\Delta b)^T\lambda.\end{aligned}$特别地, 若 $\Delta b=\epsilon e_j$, 则对充分小的 $\epsilon$, 我们有 $c^T\Delta x=\epsilon\lambda_j.$即原始问题最优目标值的改变量为 $\lambda_j$乘以 $b_j$的扰动量.

2. 可行集的几何性质

2.1 基和基本可行解

本章之后均假定 $矩阵A行满秩.$事实上, 我们可以通过预处理以移除给定约束和变量中的冗余. 经增加松弛变量、剩余变量或人工变量(artificial variables), 我们最终可使 $A$满足上述假定.
由单纯形法产生的每个迭代点称为原始问题的基本可行解(basic feasible point). $x$为基本可行解, 若存在指标集 $\{1,2,\ldots,n\}$的子集 $\mathcal{B}$使得

• $|\mathcal{B}|=m$;
• $i\not\in\mathcal{B}\Rightarrow x_i=0$(即界 $x_i\ge0$积极仅当 $i\in\mathcal{B}$);
• $m\times m$矩阵 $B=[A_i]_{i\in\mathcal{B}}$非奇异, 其中 $A_i$为 $A$的第 $i$列.

满足这些性质的 $\mathcal{B}$称作原始问题的一个基(basis). 对应的矩阵 $B$称作基矩阵(basis matrix).

仅探查基本可行解的单纯形法的大致原理是, 基本可行解序列将收敛于原始问题的解仅当

• 原始问题有基本可行解;
• 至少有一个基本可行解为基本最优解(basic optimal point). 即原始问题的解也是基本可行解.

幸运的是, 在合理假设下, 上述两条均是成立的. 这由下面的线性规划基本定理the fundamental theorem of linear programming所保证.

定理2

1. 若原始问题可行域非空, 则至少存在一个基本可行解;
2. 若原始问题有解, 则至少有一个解为基本最优解;
3. 若原始问题可行且有界, 则有一个最优解.

证明: 在所有的可行点 $x$中, 选取其中具有最小非零分量个数的, 记这一非零分量个数为 $p$. 不失一般性, 设非零分量为 $x_1,x_2,\ldots,x_p$, 因此我们有 $\sum_{i=1}^pA_ix_i=b.$假设 $A_1,A_2,\ldots,A_p$线性相关, 于是我们由它们内部的线性表示, 比方说存在 $z_1,\ldots,z_{p-1}$使得 $A_p=\sum_{i=1}^{p-1}A_iz_i.$易得对 $\forall \epsilon$, $x(\epsilon)=x+\epsilon(z_1,z_2,\ldots,z_{p-1},-1,0,0,\ldots,0)^T=x+\epsilon z$满足 $Ax(\epsilon)=b$. 另外, 由于 $x_i>0,i=1,2,\ldots,p$, 因此对于充分小的 $\epsilon$我们也有 $x_i(\epsilon)>0,i=1,2,\ldots,p$. 另方面, 存在 $\bar{\epsilon}\in(0,x_p]$使得对于某个 $i\in\{1,2,\ldots,p\}$, 有 $x_i(\bar{\epsilon})=0$. 这样, $x(\bar{\epsilon})$可行且至多有 $p-1$个非零分量, 这与我们对 $p$的选取方式是矛盾的!
这样, $A_1,A_2,\ldots,A_p$就必定是线性无关的. 从而 $p\le m$. 若 $p=m$, 则第一条得证. 此时 $x$就是基本可行解, $\mathcal{B}=\{1,2,\ldots,m\}$. 不然 $p<m$, 由于 $A$行满秩, 因此我们可从 $A_{p+1},A_{p+2},\ldots,A_n$中选取 $m-p$列与前 $p$列构成一组线性无关向量集. 再将对应的指标与 $\{1,2,\ldots,p\}$合并就得到了 $\mathcal{B}$. 这样, 第一条证明完毕.

第二条的证明是类似的. 令 $x^*$为具有最小非零分量数 $p$的解, 并设 $x_1^*,x_2^*,\ldots,x_p^*$非零. 若 $A_1,A_2,\ldots,A_p$线性相关, 我们就定义 $x^*(\epsilon)=x^*+\epsilon z,$其中 $z$的选取与之前相同. 易得 $x^*(\epsilon)$对于充分小的 $\epsilon$(不论正负)都是可行的. 由于 $x^*$最优, 必有 $c^T(x^*+\epsilon z)\ge c^Tx^*\Rightarrow \epsilon c^Tz\ge0$对充分小的 $\epsilon$均成立. 因此 $c^Tz=0$, 从而 $c^Tx^*(\epsilon)=c^Tx^*$. 我们同样也可以找到 $\bar{\epsilon}>0$使得 $x^*(\bar{\epsilon})$既可行, 有时最优, 却至多有 $p-1$个非零分量. 从而矛盾, 得出 $A_1,A_2,\ldots,A_p$必定线性无关. 利用于之前相同的推导, 我们可得到 $x^*$就是基本可行解, 从而为基本最优解.

第三条结论是单纯形法有限终止性的结论. 我们将在下一节说明之. 值得说明的是第三条才是真正可用、好用的结论: 若线性规划问题可行且有界, 则必有最优解, 从而必有解; 从第二条知, 必有基本最优解; 再从第一条知, 必有基本可行解. 因此, 在实际应用中, 检验第三条一劳永逸.

2.2 可行多面体的顶点与基本可行解

由线性约束定义的可行集是一个多面体, 其顶点为不在任何集合中两点连线上的点. 几何上, 这样的多面体结构是很直观的. 见下图.

而代数上, 这些顶点就是之前定义的基本可行解. 我们可以利用几何和代数上的对应关系来更好的理解单纯形法的工作原理. 下面证明之.

定理3 一点是可行多面体 $\{x\mid Ax=b,,x\ge0\}$的顶点当且仅当它是原始问题的基本可行解.
证明: 令 $x$为一基本可行解, 并不失一般性假设 $\mathcal{B}=\{1,2,\ldots,m\}$. 于是 $B=[A_i]_{i=1,2,\ldots,m}$非奇异, 且 $x_{m+1}=x_{m+2}=\cdots=x_n=0.$若 $x$不是可行多面体的顶点, 则 $x$必位于两可行点 $y,z$的连线上. 于是有 $\alpha\in(0,1)$使得 $x=\alpha y+(1-\alpha)z$. 因为 $y,z\ge0,\alpha,1-\alpha>0$, 所以 $y_i=z_i=0,\quad i=m+1,m+2,\ldots,n.$记 $x_B=(x_1,x_2,\ldots,x_m)^T$并类似得到 $y_B,z_B$. 我们从 $Ax=Ay=Az=b$得到 $Bx_B=By_B=Bz_B=b,$从而再由 $B$的非奇异性, 得到 $x_B=y_B=z_B$. 从而 $x=y=z$, 矛盾! 因此 $x$必是个顶点.

另一方面, 设 $x$为可行多面体的一个顶点, 且其非零分量为 $x_1,x_2,\ldots,x_p$. 若对应的列向量 $A_1,A_2,\ldots,A_p$线性无关, 我们就可类似构造向量 $x(\epsilon)=x+\epsilon z$. 因 $x(\epsilon)$对充分小的 $\epsilon$均可行, 因此可定义 $\hat{\epsilon}>0$使得 $x(\hat{\epsilon}),x(-\hat{\epsilon})$均是可行的. 由于 $x=x(0)$位于这两个点的连线上, 因此便不可能是顶点, 矛盾! 于是再次地, $A_1,A_2,\ldots,A_p$线性无关, $p\le m$. 若 $p<m$, 则可利用 $A$行满秩选取 $m-p$个指标加入 $\{1,2,\ldots,p\}$中得到 $\mathcal{B}$, 而 $x$则是对应的基本可行解. 证毕.

这样一来, 如果单纯形法的确在不断搜索基本可行解, 且能遍历, 则实际上就是在可行多面体的顶点上跳动. 由定理2, 若原始问题有解则必定有一基本最优解. 这样单纯形法必定会经有限步迭代至这一解. 进一步地, 若单纯形法是下降算法, 则就可从此解上退出.

我们引入退化的定义以结束对于可行集的几何性质的讨论. 这个术语在优化中具有多重含义, 我们后面的章节中会谈到. 而对于本章, 我们使用如下的定义:

定义1 (退化, degeneracy) 我们称基 $\mathcal{B}$是退化的, 若存在某个 $i\in\mathcal{B}$使得 $x_i=0$, 其中 $x$为对应于 $\mathcal{B}$的基本可行解; 称线性规划是退化的, 若它至少有一个退化基.

3. 单纯形法

本节我们将给出对原始问题的单纯形法的详细讨论.

3.1 概述

事实上, 单纯形法具有许多变体. 我们这里讨论的有时被称作修正单纯形法(revised simplex method). 我们将在第6节讨论对偶单纯形法(dual simplex method).

如之前所述,

• 单纯形法的迭代点均是原始问题的基本可行解, 从而也是可行多面体的顶点.
• 大多迭代步都是从一个顶点跳到一个相邻的顶点, 即前后基 $\mathcal{B}$仅相差一个分量.
• 大多数(但不是所有)迭代步下, 原始目标函数 $c^Tx$的取值都是下降的. 当然当问题无界时, 我们会得到另一种类型的迭代步: 沿着这一迭代步(也就是多面体的一边)目标函数值下降, 却永远无法到达下一个顶点.

单纯形法每步迭代的关键就是决定要移除当前基 $\mathcal{B}$中的哪一指标. 除非此步通向无界, 不然必定要从当前基 $\mathcal{B}$中移除一个指标并从基外移入一个指标. 我们可以通过KKT条件进一步了解单纯形法是如何做出这样的决策的.而且从 $\mathcal{B}$和原始问题的KKT条件, 我们不仅可以得到原始变量 $x$的值, 同时也能推得对偶变量 $(\lambda, s)$的值.

首先, 定义非基指标集 $\mathcal{N}$为 $\mathcal{B}$的补集, 即 $\mathcal{N}=\{1,2,\ldots,n\}\setminus\mathcal{B}.$类似地, 用 $N$表示非基矩阵 $N=[A_i]_{i\in\mathcal{N}}$. 将 $n$维向量 $x,s,c$依据 $\mathcal{B},\mathcal{N}$进行划分: $\begin{aligned}x_B&=[x_i]_{i\in\mathcal{B}},\quad x_N=[x_i]_{i\in\mathcal{N}},\\s_B&=[s_i]_{i\in\mathcal{B}},\quad s_N=[s_i]_{i\in\mathcal{N}},\\c_B&=[c_i]_{i\in\mathcal{B}},\quad c_N=[c_i]_{i\in\mathcal{N}}.\end{aligned}$从KKT条件可知, $Ax=Bx_B+Nx_N=b.$此时可以设当前的单纯形迭代点(即原始变量) $x$为 $x_B=B^{-1}b,\quad x_N=0.$假设我们得到的是基本可行解(此假设后面会说明可以去掉), 所以 $B$非奇异且 $x_B\ge0$, 因此这样的 $x$满足KKT条件中的等式约束条件和非负性条件.

根据互补松弛条件, 我们可设 $s_B=0$. 剩下的 $\lambda, s_N$可用稳定性条件推得: $B^T\lambda=c_B,\quad N^T\lambda+s_N=c_N.\\\Rightarrow\lambda=B^{-T}c_B.\\\Rightarrow s_N=c_N-N^T\lambda=c_N-(B^{-1}N)^Tc_B.$计算 $s_N$通常称作定价(pricing). 而 $s_N$的分量通常称作非基变量 $x_N$的机会成本(reduced costs, or opportunity costs)或影子价格.

我们唯一没有强制满足的KKT条件是对偶变量 $s$的非负性条件. 首先 $s_B$肯定是符合要求的, 因为 $s_B=0$. 若 $s_N$再符合 $s_N\ge0$, 我们就找到了最优的三元组 $(x,\lambda,s)$, 从而算法终止. 不过, 通常 $s_N$总有一个或多个分量是负的. 此时进入基 $\mathcal{B}$的指标——进基指标(entering index)(对应有进基变量(entering variable))——就选为某个 $q\in\mathcal{N}:s_q<0$. 下面我们将说明, 若允许 $x_q$为正, 则目标值 $c^Tx$会下降当且仅当

1. $s_q<0$;
2. 我们可以在增大 $x_q$的同时保持 $x$的可行性.

我们改变 $\mathcal{B}$和 $x,s$的过程叙述如下:

• 允许 $x_q$在下一步迭代增大;
• 保持 $x_N$的其他分量为0; 为保证等式约束 $Ax=b$依然成立, 讨论增大 $x_q$将会给当前的基向量 $x_B$带来多大影响;
• 持续增大 $x_q$直至 $x_B$的某个分量(比如 $x_p$)变为0, 或验证这样的分量不存在(此时问题无界);
• $p$为离基指标(leaving index)(相应有离基变量(leaving variable)), $q$为进基指标, $\mathcal{B}\leftarrow (\mathcal{B}\setminus\{p\})\cup\{q\}$.

这一选取离基和进基指标, 并对 $x,\lambda,s$进行一系列代数运算的过程, 有时称作旋转(pivoting). 下面细化旋转的代数过程.

由于新迭代点 $x^+$和当前迭代点 $x$均满足 $Ax=b$, 且由于 $x_N=0,x_i^+=0,i\in\mathcal{N}\setminus\{q\}$, 我们有 $Ax^+=Bx_B^++A_qx_q^+=Bx_B=Ax.$两边左乘 $B^{-1}$并整理可得 $x_B^+=x_B-B^{-1}A_qx_q^+.$几何上, 上式就是沿着可行多面体的一边移动, 同时减少 $c^Tx$. 继续移动直至遇到了新的顶点. 此时, 某个 $x_p\ge0$的约束积极. 我们再把这个指标 $p$从 $\mathcal{B}$中移出, 并代之以 $q$.

下面讨论目标值的变化. $c^Tx^+ =c_B^Tx_B^++c_qx_q^+=c_B^Tx_B-c_B^TB^{-1}A_qx_q^++c_qx_q^+.$之前我们有 $c_B^TB^{-1}=\lambda^T$, $A_q^T\lambda=c_q-s_q$. 因此 $c_B^TB^{-1}A_qx_q^+=\lambda^TA_qx_q^+=(c_q-s_q)x_q^+,$代入可得 $c^Tx^+=c_B^Tx_B-(c_q-s_q)x_q^++c_qx_q^+=c^Tx+s_qx_q^+.$因为 $s_q<0$, 因此只要 $x_q^+>0$, 新迭代点就能给目标值带来下降.

自然算法中 $x_q^+$是有可能一直增加到 $\infty$而从不遇到新的顶点的. 换句话说, $x_B^+=x_B-B^{-1}A_qx_q^+\ge0$对于 $x_q^+$的任意正值都成立. 此时, 线性规划无界.

下图展示了一条单纯形法在一个 $\mathbb{R}^2$中问题的迭代路径. 此例中最优解 $x^*$在三步迭代后达到.

当基 $\mathcal{B}$非退化, 我们必能保证 $x_q^+>0$, 因此会带来目标函数值 $c^Tx$的严格下降. 而若原始问题是非退化的, 则单纯形法每一步均能保证下降, 从而证明了以下单纯形法的终止定理.

定理4 若原始问题非退化且有界, 则单纯形法必将终止于一基本最优解.
证明: 由于每步迭代严格下降, 因此单纯形法不会再前后两次迭代中遍历相同的基本可行解. 而基 $\mathcal{B}$的选取方式是有限的, 且每个基对应了一个基本可行解, 这样仅有有限个基本可行解. 因此迭代有限终止. 进一步, 由于单纯形法必不可能终止于非最优基本可行解, 且问题有界, 所以必终止于基本最优解.

此定理给出了定理2第三条在线性规划非退化时的证明. 若没有非退化的假设, 单纯形法有限终止的证明要复杂得多. 我们放到第5节讨论.

3.2 单纯形法的单步迭代

事实上我们已经大致讨论了单纯形法如何具体地走出一步. 这里我们给出总结:

程序1 (One step of Simplex)
Given $\mathcal{B},x_B=B^{-1}b\ge0,x_N=0$;
Solve $B^T\lambda=c_B$ for $\lambda$,
Compute $s_N=c_N-N^T\lambda$; (pricing)
if $s_N\ge0$
$\quad\quad$step; (optimal point found)
Select $q\in\mathcal{N}$ with $s_q<0$ as the entering index;
Solve $Bd=A_q$ for $d$;
if $d\le 0$
$\quad\quad$stop; (problem is unbounded)
Calculate $x_q^+=\min_{i\mid d_i>0}(x_B)i/d_i$, and use $p$ to denote the minimizing $i$;
Update $x_B^++=x_B-dx_q^+,x_N^+=(0,\ldots,0,x_q^+,0,\ldots,0)^T$;
Change $\mathcal{B}$ by adding $q$ and removing the basic variable corresponding to column $p$ of $B$.

事实上模糊的地方还有很多, 比如我们既然保证了迭代能够保持可行性, 那么初始基应当如何选取呢? 再如若有多个 $s_q<0$, 应当选取哪个? 这在后面会有讨论.

我们用一个简单的例子阐释上述程序.

例1 考虑问题 $\begin{array}{rl}\min & -4x_1-2x_2\\\mathrm{subject\,to\,} & x_1+x_2+x_3=5,\\&2x_1+(1/2)x_2+x_4=8,\\&x\ge0.\end{array}$

• 第一步迭代, 初始基设为 $\mathcal{B}=\{3,4\}$, 此时有 $x_B=\begin{bmatrix}x_3\\x_4\end{bmatrix}=\begin{bmatrix}5\\8\end{bmatrix},\quad \lambda=\begin{bmatrix}0\\0\end{bmatrix},\quad s_N=\begin{bmatrix}s_1\\s_2\end{bmatrix}=\begin{bmatrix}-3\\-2\end{bmatrix},$以及目标函数值 $c^Tx=0$. 由于 $s_N$的两个分量都是负的, 因此指标1,2均可选择. 假设选取 $q=1$, 则 $d=(1,2)^T$, 因此不能得出问题无界. 进一步计算, 得到 $p=2$, 对应指标为4, $x_1^+=4$. 因此更新集合 $\mathcal{B}=\{3,1\},\mathcal{N}=\{4,2\}$.
• 第二步迭代, 我们有 $x_B=\begin{bmatrix}x_3\\x_1\end{bmatrix}=\begin{bmatrix}1\\4\end{bmatrix},\quad\lambda=\begin{bmatrix}0\\-3/2\end{bmatrix},\quad s_N=\begin{bmatrix}s_4\\s_2\end{bmatrix}=\begin{bmatrix}3/2\\-5/4\end{bmatrix},$以及目标函数值 $-12$. 此时 $s_N$仅有一个负分量, 对应 $q=2$. 进一步 $d=(3/2,-1/2)^T$, 同样不能得出无界. 继而 $x_2^+=4/3,p=1$, 指标3离基. 更新集合 $\mathcal{B}=\{2,1\},\mathcal{N}=\{4,3\}$.
• 第三步迭代, 我们有 $x_B=\begin{bmatrix}x_2\\x_1\end{bmatrix}=\begin{bmatrix}4/3\\11/3\end{bmatrix},\quad\lambda=\begin{bmatrix}-5/3\\-2/3\end{bmatrix},\quad s_N=\begin{bmatrix}s_4\\s_3\end{bmatrix}=\begin{bmatrix}7/3\\5/3\end{bmatrix},$以及目标函数值 $c^Tx=-41/3$. 此时 $s_N\ge0$, 从而终止.

我们需要完善以下四个重要细节:

1. 数值代数——如何高效地对 $B$进行LU分解以求解 $\lambda,d$.
2. 如何选取初始基以保证初始解的可行性.
3. 如何选取进基指标 $q$.
4. 退化基和退化迭代步如何处理. (此时无法在不打破可行性的前提下增大 $x_q^+$.)

我们在下面三节中将详细讨论上面这些问题.

4. 单纯形法中的数值代数

单纯形每步迭代均需要求解两个线性系统, 即 $B^T\lambda=c_B,\quad Bd=A_q.$为求解它们, 我们不会显式地计算 $B^{-1}$. 一般我们会计算或保持 $B$的某个分解——通常是LU分解——使用前代回代得到 $\lambda,d$. 我们知道 $B$在每步都会不同, 但差异仅仅在一列. 如果每次迭代均重新计算其分解也未免过于铺张浪费. 此时针对性的更新策略更为适宜.

标准的分解/更新程序均以单纯形法的第一步迭代中 $B$的LU分解开始. 由于一般 $B$较大而且稀疏, 为保证 $L,U$的数值稳定性和稀疏性我们必须在分解的过程中重新排列 $B$的行和列. 一种权衡这两个目标的旋转策略由Markowitz在1957提出¹, 至今仍是许多实用稀疏LU分解算法的基础. 当然也有其他的方法. 我们在这里不展开.

为简单考虑, 我们假设 $B$中已经做了行列重排, 于是有LU分解为 $LU=B,$其中 $L$为单位下三角矩阵, $U$为上三角矩阵. 之后前代回代即可得到 $\lambda,d$.
我们主要讨论 $L,U$因子如何更新, 设 $p$离基, $q$进基. 即矩阵 $B$上对应的变化就是列 $B_p$由 $A_q$代替. 经过变换的矩阵记作 $B^+$, 且注意到由 $U=L^{-1}B$, 于是 $L^{-1}B^+$将仅在第 $p$列上有所不同. 即下图所示.

接着利用一系列置换将第 $p$列移动到最后一列(第 $m$列)的位置, 并相应地将原本第 $p+1,p+2,\ldots,m$列往左移一列. 再将类似的置换应用到第 $p$至 $m$行, 其效果就是就是将非上三角的部分移到矩阵的最后一行. 最终效果如下.

最后, 对矩阵 $P_1L^{-1}B^+P_1^T$作稀疏Gauss消去以储存上三角的形式. 即求得 $L_1,U_1$使得 $P_1L^{-1}B^+P_1^T=L_1U_1.$易验证 $L_1,U_1$形式是简单的. 具体说来: 下三角矩阵 $L_1$与单位阵仅在最后一行不同, 而 $U_1$则除了在 $(m,m)$元上的改变以及最后一行的非对角元的消去, 与 $P_1L^{-1}B^+P_1^T$是相同的.

我们以 $m=5$举例, 使用以下记号: $L^{-1}B=U=\begin{bmatrix}u_{11} & u_{12} & u_{13} & u_{14} & u_{15}\\ & u_{22} & u_{23} & u_{24} & u_{25} \\ & & u_{33} & u_{34} & u_{35}\\ & & & u_{44} & u_{45}\\ & & & & u_{55}\end{bmatrix},\quad L^{-1}A_q=\begin{bmatrix}w_1\\w_2\\w_3\\w_4\\w_5\end{bmatrix},$假设 $p=2$, 于是 $L^{-1}B^+=\begin{bmatrix}u_{11} & w_1 & u_{13} & u_{14} & u_{15}\\ & w_2 & u_{23} & u_{24} & u_{25}\\& w_3 & u_{33} & u_{34} & u_{35}\\& w_4 & & u_{44} & u_{45}\\ & w_5 & & & u_{55}\end{bmatrix}.$在经过置换 $P_1$后, 我们有 $P_1L^{-1}B^+P_1^T=\begin{bmatrix}u_{11} & u_{13} & u_{14} & u_{15} & w_1\\& u_{33} & u_{34} & u_{35} & w_3\\& & u_{44} & u_{45} & w_4\\& & & u_{55} & w_5\\& u_{23} & u_{24} & u_{25} & w_2\end{bmatrix}.$于是因子 $L_1,U_1$如下: $L_1=\begin{bmatrix}1 & & & &\\ & 1 & & &\\& & 1 & & \\& & & 1 &\\0 & l_{52} & l_{53} & l_{54} & 1\end{bmatrix},\quad U_1=\begin{bmatrix}u_{11} & u_{13} & u_{14} & u_{15} & w_1\\& u_{33} & u_{34} & u_{35} & w_3\\& & u_{44} & u_{45} & w_4\\& & & u_{55} & w_5\\ & & & & \hat{w_2}\end{bmatrix}.$利用 $P_1L^{-1}B^+P_1^T$的分解, 我们有 $B^+=L^+U^+,\quad 其中L^+=LP_1^TL_1,\quad U^+=U_1P_1.$我们不需要显式地计算 $L^+,U^+$. $L_1$中的非零元和 $U_1$的最后一列以及置换信息 $P_1$均可以用紧形式(compact form)储存, 从而涉及 $L^+,U^+$的代换操作可通过一系列与它们相关的置换和稀疏三角阵代换实现. 而之后的迭代也以类似地方式更新和进行.

上面我们所介绍的程序十分高效, 因为它在每步迭代更新时仅需储存极少的数据, 并且无需较多移动内存中的数据. 其主要缺陷在于可能存在的数值不稳定. 矩阵分解因子中的大数值往往是数值不稳定的诱因, 而这里 $L_1$中的元素(比如 $l_{52}$)就有可能非常大. 早期的程式会通过重排行向量来避免这个问题. 例如, 当 $|u_{33}|<|u_{23}|$, 我们就交换第2行和第5行以保证之后计算的 $l_{52}$不超过1. 这可以带来数值稳定性, 但却可能使上三角因子的右下角在更新过程中变得稠密.

尽管每次迭代的更新信息(置换矩阵和稀疏三角因子)可以用高度紧致的形式储存, 但多次更新后它们所占用的空间会达到无法容忍的水平. 同时, 用于求解程序1中向量 $d,\lambda$的时间也在攀升. 而若更新过程不够稳定, 数值误差也会进入其中, 并进一步影响之后的算法进程. 基于这些原因, 大多数单纯形法的实施将周期性地重新计算当前基矩阵 $B$的LU分解, 摒弃之前积累的更新信息. 而之后的策略与开始相同. 这就在一定程度上平衡了数值稳定性、稀疏性和结构的需求.

5. 其他重要的细节

5.1 定价和进基指标的选取

通常每步 $s_N$有许多负的分量. 我们应当如何从这些对应的指标中选取合适的进基呢? 最理想的状态下, 我们希望选取的指标列能使算法在最少的迭代步下收敛到解 $x^*$, 但我们往往不具有这样的全局观念或信息. 因此我们常用一种更加"短视"但却较为实用的策略以得到在当前迭代中目标函数值 $c^Tx$的显著下降. 一般地, 在选取好的进基指标上所做的花费与后续在目标函数值上达到的下降存在某种均衡. 不同的旋转策略以不同的方式达成均衡.

5.1.1 Dantzig的选取方式

Dantzig最原始的选取方式是最简单的一种: 选取 $q$使得 $s_q$为 $s_N=N^T\lambda$中最小的分量. 这一选取方法基于此前得到的目标函数值的下降公式 $c^Tx^+-c^Tx=s_qx_q^+.$因此这样能在进基变量 $x_q$每增加一个单位时, 给 $c^Tx$带来最大的下降. 但这仅仅是类似于导数的观点. 实际上我们可能无法达成较大的下降, 这是因为在到达下一个顶点时, $x_q^+$可能仅仅只能增加增加一个小量.

5.1.2 部分定价与多次定价策略

计算完整的 $s_N$需要计算 $N^T$与一个向量的乘积, 这在矩阵 $N$很大时是很昂贵的. 相比之下, 部分定价策略partial pricing strategies仅仅计算 $s_N$的一个子向量, 并根据这一子向量的负分量决定进基变量. 为给予 $\mathcal{N}$中所有的指标进基的机会, 这些策略将循环遍历非基元素, 周期地改变所计算的 $s_N$子向量.

这些策略均不能保证我们能沿着选取的边在到达新顶点前, 获得大量的函数值下降. 而多次定价策略multiple pricing strategies则更加全面: 对于 $\mathcal{N}$的一个小子集, 其中的 $q\in\mathcal{N}$, 它们计算 $s_q$且若 $s_q<0$, 则再计算 $x_q^+$的最大可行值和目标函数值的后续下降 $s_qx_q^+$. $x_q^+$的计算需要计算 $d=B^{-1}A_q$, 这并不经济. 后续迭代将一直处理同样的指标集直至此集中所有的 $s_q$均非负. 此时计算完整的 $s_N$, 选取全新的非基指标子集并开启新的一轮循环迭代. 这种方法的优点在于, 矩阵 $N$中当前定价分量子集以外的列是不需要的, 因此实施过程中的内存使用会被大大降低.自然我们也可以设计结合部分和多次定价策略的启发式算法.

5.1.3 最速下降边策略

一种称为是**最速下降边(steepest edge)**的策略选取所有候选中的"最速下山(most downhill)"方向——沿边移动单位长度能带来 $c^Tx$的最大下降. 注意Dantzig的选取法则是 $x_q^+$每增加一个单位, $c^Tx$能下降得最多. 而 $x_q^+$增加的小量可能对应沿着边走的一大步. 因而二者是不尽相同的. 在旋转步中, $x$变为 $x^+=\begin{bmatrix}x_B^+\\x_N^+\end{bmatrix}=\begin{bmatrix}x_B\\x_N\end{bmatrix}+\begin{bmatrix}-B^{-1}A_q\\e_q\end{bmatrix}x_q^+=x+\eta_qx_q^+,$其中 $e_q$是只在位置 $q\in\mathcal{N}$为1, 其他位置为0的单位向量, 而 $\eta_q$定义为 $\eta_q=\begin{bmatrix}-B^{-1}A_q\\e_q\end{bmatrix}=\begin{bmatrix}-d\\e_q\end{bmatrix};$沿着 $\eta_q$移动单位长度, $c^Tx$的下降为 $-\frac{c^T\eta_q}{\Vert\eta_q\Vert}.$而最速下降边策略就是要选取极大化这个量的指标 $q\in\mathcal{N}$.

若我们必须通过求解 $Bd=A_i,i\in\mathcal{N}$以得到每个 $\eta_i$, 最速下降边策略无疑是昂贵的. 不过事实上, 每步迭代, 所有的 $i\in\mathcal{N}$沿边下降的度量 $\frac{c^T\eta_q}{\Vert\eta_q\Vert}$均可以用一种经济的方式更新. 下面我们大致介绍如何在每步迭代更新 $c^T\eta_i,\Vert\eta_i\Vert$.

首先, 注意到我们无需计算 $\eta_i$就已经有了分子 $c^T\eta_i$, 这是因为由先前 $c^Tx$上的下降公式 $c^Tx^+-c^Tx=s_qx_q^+,$再比对即可得 $c^T\eta_i=s_i.$ 为得到当前步下分母 $\Vert\eta_i\Vert$的改变, 我们定义 $\gamma_i=\Vert\eta_i\Vert^2$, 于是在更新前后 $\gamma_i$分别为 $\begin{aligned}\gamma_i&=\Vert\eta_i\Vert^2=\Vert B^{-1}A_i\Vert^2+1,\\\gamma_i^+&=\Vert\eta_i^+\Vert^2=\Vert(B^+)^{-1}A_i\Vert^2+1.\end{aligned}$不失一般性, 假设进基列 $A_q$替换了基矩阵 $B$的第一列, 即 $p=1$, 且此列对应指标 $t$. 于是 $B^+$可写作: $B^+=B+(A_q-A_t)e_1^T=B+(A_q-Be_1)e_1^T.$利用秩一修正的Sherman-Morrison-Woodbury公式, 我们有 $(B^+)^{-1}=B^{-1}-\frac{(B^{-1}A_q-e_1)e_1^TB^{-1}}{1+e_1^T(B^{-1}A_q-e_1)}=B^{-1}-\frac{(d-e_1)e_1^TB^{-1}}{e_1^Td}.$因此 $(B^+)^{-1}A_i=B^{-1}A_i-\frac{e_1^TB^{-1}A_i}{e_1^Td}(d-e_1).$将 $(B^+)^{-1}A_i$的表达式代入 $\gamma_i^+$的计算式, 整理可得 $\gamma_i^+=\gamma_i-2\left(\frac{e_1^TB^{-1}A_i}{e_1^Td}\right)A_i^TB^{-T}d+\left(\frac{e_1^TB^{-1}A_i}{e_1^Td}\right)^2\gamma_q.$若求得以下两个线性系统得到 $\hat{d},r$: $B^T\hat{d}=d,\quad B^Tr=e_1,$则 $\gamma_i$的更新公式为 $\gamma_i^+=\gamma_i-2\left(\frac{r^TA_i}{r^TA_q}\right)\hat{d}^TA_i+\left(\frac{r^TA_i}{r^TA_q}\right)^2\gamma_q.$因此, 对于 $i\ne q$的 $\gamma_i$, 仅需求解两个(相比于之前需要对每个 $i$求解 $Bd=A_i$)线性系统并对每个 $i$计算内积 $r^TA_i,\hat{d}^TA_i$.

最速下降边策略并不保证我们能在到达另一个顶点前走一大步, 但在实际应用中它表现得相当高效.

5.2 确定单纯形法初始步的两阶段法

单纯形法需要人为给定初始的基本可行解 $x$和对应的初始基 $\mathcal{B}\subset\{1,2,\ldots,n\}:|\mathcal{B}|=m$, 使得基矩阵 $B$非奇异且 $x_B=B^{-1}b\ge0, x_N=0$. 寻求初始解和基的问题可能本身就非平凡——事实上, 其难度相当于求解一个线性规划. 这里我们介绍在实际实施中经常用到的两阶段法(two-phase approach).

第一阶段(Phase I), 我们基于原始数据构建一个辅助线性系统, 并使用单纯形法求解之. 第一阶段问题的初始基和初始基本可行解必须是平凡的, 其解又给第二阶段(Phase II)提供了初始的基本可行解. 而在第二阶段, 我们要求解一个类似于原始问题的线性规划. 原始问题的解可以从第二阶段问题的解中容易地获取.

5.2.1 第一阶段

在第一阶段, 我们将人工变量 $z$引入原始问题并重新定义目标函数为这些人工变量的和: $\min e^Tz,\quad \mathrm{subject\,to\,}Ax+Ez=b,(x,z)\ge0,$其中 $z\in\mathbb{R}^m,e=(1,1,\ldots,1)^T$, $E$为对角阵, 其对角元为 $E_{jj}=+1,\quad b_j\ge0;\quad E_{jj}=-1,\quad b_j<0.$注意到人工变量与松弛变量的不同: 松弛变量的引入使得前后约束是等价的, 而人工变量引入后是不等价的. 易得第一阶段问题平凡的基本可行解 $x=0,z_j=|b_j|,\quad j=1,2,\ldots,m.$在第一阶段问题的每一个可行点, 人工变量 $z$都代表约束 $Ax=b$被 $x$分量违反的程度. 而目标函数就是这些违反度的和, 因此通过极小化此和, 我们就强迫 $x$成为原始问题的可行解. 易知第一阶段问题有一最优目标值为0当且仅当原始问题可行.
在第一阶段中, 我们从初始解开始应用单纯形法求解. 此线性规划下有界为0, 因此假设单纯形法不循环(我们后面会谈到循环, 也就是退化的问题), 则它必将终止于最优解. 若在最优解处 $e^Tz$为正, 则原始问题不可行; 否则单纯形法就得到了 $(\tilde{x},\tilde{z}):e^T\tilde{z}=0$, 这恰好就是下述第二阶段问题的一个初始基本可行解: $\min c^Tx,\quad\mathrm{subject\,to\,}Ax+z=b,\quad x\ge0,\quad 0\ge z\ge0.$注意与第一阶段相比, 第二阶段问题的目标函数换回了 $c^Tx$, 且 $z$有了上界 $0$的约束. 事实上, 易知第二阶段问题与原始问题是等价的. 然而我们在第二阶段中必须保留人工变量 $z$, 这是因为 $z$的某些分量仍可能出现在第二阶段的初始基中, 尽管这些分量 $\tilde{z}_j$必定是0. 而这个初始基正是从第一阶段的最优基继承下来的. 事实上, 我们可以仅考虑在基中的 $z$的分量构成的第二阶段问题.

5.2.2 第二阶段

第二阶段问题由于 $z$的上下界约束同时存在显得并不是十分标准. 但我们可以使用本章最前面讲述的方法处理之. 这样原始的单纯形法便可以使用. 进一步地, 我们也可以稍微改变单纯形法, 使得一旦 $z$有分量离基, 就将其对应的信息从第二阶段的问题中删除以减小问题规模, 简化存储. 这样也防止同一指标反复进基、离基的现象出现.

若 $(x^*,z^*)$为第二阶段问题的基本解, 则必有 $z^*=0$, 从而 $x^*$为原始问题的一解. 并且事实上, $x^*$是原始问题的基本可行解, 尽管第二阶段问题最终的基 $\mathcal{B}$可能仍含有 $z^*$中的分量. 但因为 $A$行满秩, 我们可以通过后处理postprocessing得到原始问题的最优基: 将 $\mathcal{B}$中所有当前 $z$的分量剔除, 并代之以 $x$中的非基分量, 同时保持 $B$的非奇异性(实际上就是扩基).

5.2.3 注意点与示例

最后值得注意的是, 在许多问题中我们无需添加全部 $m$个人工变量构造第一阶段问题. 这在松弛和剩余变量已经显式地存在于问题中时显得尤为突出, 例如原始问题为 $\min c^Tx,\quad\mathrm{subject\,to\,}Ax+z=b,z\ge0.$此时我们要得到具有标准形式的线性规划. 这时候一些松弛/剩余变量就能充当人工变量, 我们就无需再显式地添加这样的变量徒增计算量.

下面我们以一个例子阐释这一点.

例2 考虑带不等式约束的线性规划问题: $\begin{array}{rl}\min & 3x_1+x_2+x_3\\\mathrm{subject\,to} & 2x_1+x_2+x_3\le2,\\&x_1-x_2-x_3\le-1,\\&x\ge0.\end{array}$对两个不等式约束都增加松弛变量, 我们得到了如下等价的标准形式: $\begin{array}{rl}\min & 3x_1+x_2+x_3\\\mathrm{subject\,to}&2x_1+x_2+x_3+x_4=2,\\&x_1-x_2-x_3+x_5=-1,\\&x\ge0.\end{array}$在构建第一阶段问题时, 注意到 $x_4$已经能充当第一个约束的人工变量了, 因此我们仅需增加一个人工变量 $z_2$并得到第一阶段问题: $\begin{array}{rl}\min & z_2\\\mathrm{subject\,to} & 2x_1+x_2+x_3+x_4=2,\\&x_1-x_2-x_3+x_5-z_2=-1,\\&(x,z_2)\ge0.\end{array}$易得 $(x,z_2)=((0,0,0,2,0),1)$为第一阶段问题的基本可行解, 这是因为相应的基矩阵 $B$为 $B=\begin{bmatrix}1 & 0\\0 & -1\end{bmatrix}.$

5.3 退化步和循环现象

如前所述, 单纯形法可能会遇到这样的困境: 对于进基指标 $q$, 我们无法在不打破条件 $x^+\ge0$的前提下增大 $x_q^+$. 参考程序1, 我们知道这样的情形发生仅当存在 $i$使得 $(x_B)_i=0,d_i<0$. 这样的迭代步称为退化步(degenerate steps). 在这样的迭代步上, $x$的分量将不会变化, 从而不改变目标函数值. 但这样的迭代步仍可能是有用的, 至少它们改变了当前的基 $\mathcal{B}$, 而我们期望改变后的 $\mathcal{B}$离最优基又更近了一步. 换句话说, 退化步的出现可能为 $c^Tx$的下降埋下了伏笔.

但有些时候, 循环cycling现象会发生: 在连续几次退化步后, 我们可能又回到了之前的基 $\mathcal{B}$. 如果仍然使用相同的策略选取进基和离基的指标, 算法就会无穷循环下去, 永不收敛.

循环一度被视作是一种罕见的现象, 直至近期它频繁地出现于一些大型线性规划(来自于整数规划的松弛)的求解中. 由于整数规划是线性规划的一个重要源头, 因此实用的单纯形算法往往会包含规避循环的策略.

在本节接下来的内容里, 我们将介绍两种策略以应对循环: 约束扰动策略perturbation strategy和它的"近亲", 字典顺序策略(lexicographic order strategy).

5.3.1 约束扰动策略

假设在某一单纯形迭代步上算法遇到了退化基 $\hat{\mathcal{B}}$和退化基矩阵 $\hat{B}$. 这是我们在原始问题的约束右端添加一个小扰动, 得到修正的线性规划: $b(\epsilon)=b+\hat{B}\begin{bmatrix}\epsilon\\\epsilon^2\\\vdots\\\epsilon^m\end{bmatrix},$其中 $\epsilon$为一很小的正数. 这就带来了基本解向量分量上的改变: $x_{\hat{B}}(\epsilon)=x_{\hat{B}}+\begin{bmatrix}\epsilon\\\epsilon^2\\\vdots\\\epsilon^m\end{bmatrix}.$保留这一扰动, 我们可得后续的基本解具有形式 $x_B(\epsilon)=x_B+B^{-1}\hat{B}\begin{bmatrix}\epsilon\\\epsilon^2\\\vdots\\\epsilon^m\end{bmatrix}=x_B+\sum_{k=1}^m(B^{-1}\hat{B})_{\cdot k}\epsilon^k,$其中 $(B^{-1}\hat{B})_{\cdot k}$表示 $B^{-1}\hat{B}$的第 $k$列, $x_B$表示未经扰动的解.

对于充分小的 $\epsilon$, $(x_{\hat{B}}(\epsilon))_i>0, \forall i$. 因此 $\mathcal{\hat{B}}$为扰动问题的非退化基. 这就可以为目标值带来非零的(但很小)的下降.

事实上, 若保留扰动, 且 $\epsilon$足够小(不固定), 我们断言算法经历的所有基均是非退化的. 下面反证, 假设存在某个即 $B$使得对于某个 $i$, $(x_B(\epsilon))_i=0, \forall\epsilon$充分小. 从 $x_B(\epsilon)$的表达式我们可以看到, 此情形发生仅当 $(x_B)_i=0,(B^{-1}\hat{B})_{ik}=0,k=1,2,\ldots,m$. 这说明 $B^{-1}\bar{B}$的第 $i$行全0, 这与 $B,\hat{B}$均非奇异矛盾.
于是我们可得出结论, 只要初始 $\epsilon$选的足够小使得所有后续的基均不退化, 则单纯形法对每个基的遍历次数至多为1. 因此由定理4的证明, 单纯形法将有限终止于扰动问题的解. 而扰动可通过后处理去除: 对最后的基 $B$置 $x_B=B^{-1}b$, 这里 $b$为原始的约束右端.

5.3.2 字典顺序策略

现在的问题在于当头一次遇到退化基 $\hat{\mathcal{B}}$时, 如何选取充分小的 $\epsilon$. 字典顺序策略中不会显式的选取 $\epsilon$, 而是追踪每个基变量对相应 $\epsilon$的幂次的依赖程度. 当要选取离基变量, 它将选取 $p$为在基的所有分量中极小化 $(x_B(\epsilon))_i/d_i,\forall\epsilon$充分小的指标. 类似于之前对每个基非退化的反证, 我们亦可以说明这样选取的 $p$是唯一的. 我们可以稍微拓展旋转程序来在每步迭代, 更新每个基变量(包括刚进基的变量 $x_q$)对 $\epsilon$幂次的依赖程度.

6. 对偶单纯形法

本节我们介绍另一种单纯形法的变体——对偶单纯形法(the dual simplex method). 它适用于许多场景并且往往在许多实际问题中要快于上面的修正单纯形法.

对偶单纯形法的术语和方法与修正单纯形法有许多相似之处, 例如要将矩阵 $A$分裂成两个列子阵 $B,N$, 并且要迭代产生满足互补松弛条件的 $x^Ts=0$的三元组 $(x,\lambda,s)$.
不同之处在于,

• 第3节中的修正单纯形法从一个可行的 $x(x_B\ge0,x_N=0)$和对应的对偶变量 $(\lambda,s):s_B=0,s_N$不必非负出发. 在进行一系列 $B,N$之间的列交换后, 修正修正单纯形法将得到对偶变量 $(\lambda,s):s_N\ge0$, 从而得到原始问题(同时也是对偶问题)的解.
• 对偶单纯形法以对偶问题的视角, 从可行的对偶变量 $(\lambda,s):s_N\ge0,s_B=0$和对应的原始可行解 $x:x_N=0,x_B$不必非负出发. 通过一系列 $B,N$之间的列交换, 最终得到原始可行解 $x:x_B\ge0$, 从而满足最优性. 注意尽管 $B$为 $A$的非奇异列子阵, 但我们不能再把它称为基矩阵, 这是因为在迭代的过程中不再保证(原始)可行条件 $x_B=B^{-1}b\ge0$.

我们现在描述对偶单纯形法如何走出单次迭代步. 尽管与第3节相似, 但这里还是有些更复杂的细节需要注意. 首先对于子阵 $B,N$(对应的指标集 $\mathcal{B},\mathcal{N}$), 我们定义当前与之对应的原始和对偶变量: $x_B=B^{-1}b,\quad x_N=0,\\\lambda=B^{-T}c_B,\\s_B=c_B-B^T\lambda=0,\quad s_N=c_N-N^T\lambda\ge0.$若 $x_B\ge0$, 则当前的三元组 $(x,\lambda,s)$就满足最优性KKT条件, 算法终止. 若不然, 选取立即指标 $q\in\mathcal{B}:x_q<0$. 我们的目的是把 $x_q$变为0, 同时允许 $s_q$增大. 我们也需要确定进基指标 $r\in\mathcal{N}$使得 $s_r$在此步后变为0而 $x_r$增大. 之后用原本 $\mathcal{N}$中的 $r$代替原本 $\mathcal{B}$中的 $q$.

那么同样地, 我们应当如何选取 $r$, 进一步 $x,\lambda,s$会如何变化? 下面我们以 $(x+,\lambda^+,s^+)$表示迭代之后的三元组.

• $\lambda,s$的变化. 由于我们是要增大 $s_q$, 而保持其他的 $s_B=0$, 因此更新后的 $s_B^+$具有形式 $s_B^+=s_B+\alpha e_q.$这里 $\alpha$为待定的正标量. 我们将 $\lambda$的更新写作 $\lambda^+=\lambda+\alpha v,$其中 $v$为一待定的向量. 事实上, 由于 $s_B^+,\lambda^+$必须满足 $s_B^+=c_B-B^T\lambda^+=0,$因此我们有 $s_B+\alpha e_q=c_B-B^T(\lambda+\alpha v)\\\Rightarrow e_q=-B^Tv,$这样我们可以求得 $v$. 对偶目标函数值 $b^T\lambda$将作如下变化: $\begin{aligned}b^T\lambda^+&=b^T\lambda+\alpha b^Tv\\&=b^T\lambda-\alpha b^TB^{-T}e_q\\&=b^T\lambda-\alpha x_B^Te_q\\&=b^T\lambda-\alpha x_q.\end{aligned}$由于 $x_q<0$, 且由于我们是要尽可能地极大化对偶目标, 我们自当希望能够选取 $\alpha$越大越好. 同时 $\alpha$的上界将由 $s_N^+\ge0$给出. $s_N^+=c_N-N^T\lambda^+=s_N-\alpha N^Tv=s_N-\alpha w,$其中 $w=N^Tv=-N^TB^{-T}e_q.$因此 $\alpha$最多能取到 $\alpha=\min_{j\in\mathcal{N},w_j>0}\frac{s_j}{w_j}.$定义进基指标 $r$为上述最小值达到的位置. 因此 $s_r^+=0,\quad w_r=A_r^Tv>0.$
• $x$的变化. 对离基指标 $q$, 我们需设定 $x_q^+=0$, 而对于进基指标 $r$, 我们允许 $x_r^+$非零. 我们记 $x_B$的变化方向向量为 $d:$ $x_B^+=x_B+\hat\gamma d.$则应有 $\begin{aligned}Bx_B=b&=Bx_B^++A_rx_r^+\\&=B(x_B+\hat\gamma d)+A_rx_r^+.\end{aligned}$简单起见, 定义 $d:$ $Bd=\sum_{i\in\mathcal{B}}A_id_i=A_r.$由于 $\sum_{i\in\mathcal{B}}A_ix_i=b,$因此 $\sum_{i\in\mathcal{B}}A_i(x_i-\gamma d_i)+A_r\gamma=b,\forall\gamma.$为确保 $x_q^+=0$, 置 $\gamma=\frac{x_q}{d_q},$这在 $d_q$非零时是良定的. 事实上我们必有 $d_q<0:$ $d_q=d^Te_q=A_r^TB^{-T}e_q=-A_r^Tv=-w_r<0.$而又因 $x_q<0$, 因此 $\gamma>0$. 这也正好满足了 $x_r>0$的需求. 于是我们可定义 $x^+$为 $x_i^+=\left\{\begin{array}{ll}x_i-\gamma d_i, & i\in\mathcal{B},i\ne q,\\0, & i=q,\\0, & i\in\mathcal{N},i\ne r,\\\gamma, & i=r.\end{array}\right.$

7. 预解

预解(presolving)(也称为预处理(preprocessing))常见于使用的线性规划算法中, 以减小用户定义的线性规划问题的规模, 再将问题传入求解器中. 在这里, 各种各样的技巧(有的很显然, 有的很巧妙)被用来消去特定的变量、约束. 通常约减的规模会十分夸张, 从而用于预解问题的线性规划算法所需时间将会大大减少. 预解这一过程是不论算法的. 事实上它在单纯形法和内点法中都有用到. 同时预解器也可探查不可行性的存在, 从而根本无需调用线性规划的算法.

我们在这仅介绍一些较为直接的预处理技巧. 为讨论方便, 假设线性规划具有上下界约束: $\min c^Tx,\quad\mathrm{subject\,to\,}Ax=b,l\le x\le u,$其中 $l$的分量允许为 $-\infty$, $u$的分量允许为 $+\infty$.

• 行单元格row singleton的情形, 即有一个等式约束仅与一个变量有关. 具体地, 若约束 $k$仅与变量 $j$有关(即 $A_{kj}\ne0$, 但 $A_{ki}=0,i\ne j$), 立可得 $x_j=b_k/A_{kj}$从而消去了问题中的 $x_j$. 若 $x_j$的这一值违反了界的约束, 我们就知道这个问题不可行, 算法终止.
• 自由列单元格free column singleton的情形, 即有一变量 $x_j$仅在一个等式约束中存在, 且自由(无界的约束). 此时对某个 $k$有 $A_{kj}\ne0$, 而 $A_{lj}=0,l\ne k$. 因此我们可以用约束 $k$来消去 $x_j$: $x_j=\frac{b_k-\sum_{p\ne j}A_{kp}x_p}{A_{kj}}.$只要约减线性规划中的 $x_p,p\ne j$被求解出来, 我们就可回代得到 $x_j$. 注意这一过程若 $c_j\ne0$则需要改变 $c$: $c_p\leftarrow c_p-c_jA_{kp}/A_{kj},\quad p\ne j.$此时我们亦可决定出对应于约束 $k$的对偶变量. 由于 $x_j$为自由变量, 因此无对应松弛变量, 从而第 $j$个对偶约束变为 $\sum_{l=1}^mA_{lj}\lambda_l=c_j\Rightarrow A_{kj}\lambda_k=c_j,$这样就有 $\lambda_k=c_j/A_{kj}$.
• 零行零列zero rows and columns的情形. 这是最简单的. 若 $A_{ki}=0,i=1,2,\ldots,n$且右端 $b_k=0$, 我们就可以直接删去这一行, 对应地置Lagrange乘子 $\lambda_k$为任意值. 而对于零列, 比如 $A_{kj}=0,k=1,2,\ldots,m$, 我们就可根据对应的成本系数 $c_j$和界 $l_j,u_j$得到 $x_j$的最优值. 若 $c_j<0$, 则 $x_j=u_j$以极小化 $c_jx_j$. 若 $c_j<0,u_j=+\infty$, 则问题无界. 类似地, 也有对 $c_j>0$的讨论.
• 存在强迫或占主的约束forcing or dominated constraints的情形. 我们不给出一般形式的讨论, 而打算通过一个简单的例子阐述. 强迫约束的例子: 假设有一等式约束为 $5x_1-x_4+2x_5=10,$其中变量有界 $0\le x_1\le 1,\quad -1\le x_4\le 5,\quad 0\le x_5\le 2.$不难发现只有当 $x_1,x_5$取上界而 $x_4$取下界时等式约束才成立. 因此可置 $x_1=1,x_4=-1,x_5=2$并消去变量、约束.
  占主约束的例子: 假设有等式约束 $2x_2+x_6-3x_7=8,$其中变量有界约束 $-10\le x_2\le 10,\quad 0\le x_6\le 1,\quad 0\le x_7\le2.$重新整理约束并利用 $x_6,x_7$的界, 我们有 $x_2=4-(1/2)x_6+(3/2)x_7\le4-0+(3/2)2=7.$另一方向可得 $x_2\ge7/2$. 这就说明 $x_2$的界 $-10,10$是冗余的, 它内蕴地含在由 $x_6,x_7$决定的区间内. 基于这一关系, 我们就可将 $x_2$视作自由变量.

预解程序是递归调用的, 这是因为一些特定变量或约束的消去可能会出发更多的消去. 例如当前问题具有两个等式约束 $3x_2=6,\quad x_2+4x_5=10.$第一个约束是行单元格, 于是有 $x_2=2$, 可消去 $x_2$和第一个约束. 代换后, 第二个约束变成 $4x_5=10-x_2=8$, 这又是个行单元格. 可以预见, 当约束矩阵内包含三角形式时预解将会尤其有用.

8. 如何看待单纯形法

在线性规划中, 正如所有带不等式约束的优化问题, 算法的基本任务是要确定这些约束中哪些是在解上起作用的. 事实上, 单纯形法从属于更大的一类处理约束优化问题的算法——积极集法(active set methods)——它显式地保有对积极和非积极指标的估计, 并在算法的每一步迭代更新. 对于单纯形法, 基 $\mathcal{B}$就是我们当前对非积极集的估计. 而单纯形法也如大多积极集法一样, 它在每步仅对指标集做较为微小的改动——交换 $\mathcal{B},\mathcal{N}$的单个元素.

二次规划、界约束优化和非线性规划的积极集法使用与单纯形法相同的基本策略: 显式地估计积极集, 并基于估计构造**既约问题(reduced problem)**求得迭代步. 在约束非线性的情形, 单纯形的许多优良性质都不再成立. 例如一般不再有至少 $n-m$个 $x$的分量为0; 第5节中的数值代数不再适用. 尽管如此, 单纯形法依然被视为约束优化积极集法的前身.

单纯形法的一个不良特征在其发展早期便引发了相当的关注. 尽管在大多数实际问题上表现得很高效(算法一般需要至多 $2m$到 $3m$次迭代, 其中 $m$为约束矩阵的行数), 但它在一些病态问题上却总是差强人意. Klee和Minty提出了一个 $n$维问题(Klee-Minty反例), 它的可行多面体具有 $2^n$个顶点, 而单纯形法在达到最优点前总会遍历其他顶点! Klee-Minty反例说明, 单纯形法的复杂度可以是指数级的——粗略地说, 其运行时间可能是问题维度的指数函数. 多年来, 理论研究者都在探寻具有多项式复杂度(polynomial complexity)的线性规划算法, 即运行时间由问题所需存储量的一个多项式函数所界定. 在上世纪七十年代末, Khachiyan给出了一种具多项式复杂度的椭圆方法(ellipsoid method), 但这一方法并不实际. 上世纪八十年代中期, Karmarkar得到了一个多项式复杂度的算法²——它不沿着单纯形的边界走向解, 而是从可行多面体的内部趋近解. Karmarkar提出的方法标志着内点法(interior-point methods)的开端, 我们将在下一章介绍之.

---

1. Markowitz, Harry M . The Elimination form of the Inverse and its Application to Linear Programming[J]. Management Science, 1957, 3(3):255-269. ↩︎

2. Karmarkar N . A new polynomial-time algorithm for linear programming[J]. Combinatorica, 1984, 4(4):373-395. ↩︎