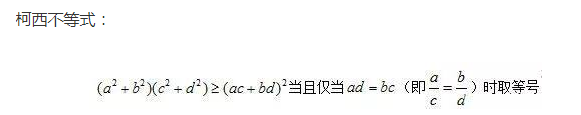Unconstrained and Constrained Optimization

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/bryant_meng/article/details/99703915

1 无约束的最优化问题

无约束优化问题是机器学习中最普遍、简单的优化问题。

$x^{*}=\underset{x}{min}f(x),x\in \mathbb{R}^n$

1.1 梯度下降法

最常见的是梯度下降法，eg： $f(x,y) = x^2+y^2$

等高线

为什么梯度是上升最快的方向呢？我们来探讨一下：

假设我们要从 $P$ 点出发，移动固定长度 $L$，到达点 ${P}'$，往哪个方向走函数值增长最快呢？

我们先定义单位长度的变化量为：

$\frac{f(x_0+Lcos\theta, y_0+Lsin\theta) - f(x_0,y_0)}{L}$

化简一下，当 L 非常小，趋于 0 的时候：

$\begin{aligned} &= \lim_{L \to 0}\frac{f(x_0+Lcos\theta, y_0+Lsin\theta) - f(x_0 + Lcos\theta,y_0)}{L} + \lim_{L \to 0}\frac{ f(x_0 + Lcos\theta,y_0) - f(x_0,y_0)}{L}\\ & = \lim_{L \to 0}sin\theta\frac{f(x_0+Lcos\theta, y_0+Lsin\theta) - f(x_0 + Lcos\theta,y_0)}{Lsin\theta} + \lim_{L \to 0}cos\theta\frac{ f(x_0 + Lcos\theta,y_0) - f(x_0,y_0)}{Lcos\theta}\\ & = sin\theta {f_y}'(x_0+Lcos\theta,y_0) +cos\theta {f_x}'(x_0,y_0)(当 L 趋于 0 时) \\ & = sin\theta {f_y}'(x_0,y_0) +cos\theta {f_x}'(x_0,y_0) \end{aligned}$

问题转化为当 $\theta$ 为多少的时候，单位变化的最多

向量内积
$m \cdot n = |m||n|cos\theta$

平方一下
$(m \cdot n)^2 = |m|^2|n|^2cos^2\theta \leq |m|^2|n|^2$

哈哈哈，这就是柯西不等式，m为 (a,b)，n为 (c,d)！

如果向量 m 为 $(cos\theta,sin\theta)$，向量 n 为 $({f_x}'(x_0,y_0),{f_y}'(x_0,y_0))$，那么
$[cos\theta {f_x}'(x_0,y_0)+sin\theta {f_y}'(x_0,y_0) ]^2 \leq (cos^2\theta + sin^2\theta)([{f_x}'(x_0,y_0)]^2+[{f_y}'(x_0,y_0)]^2) = [{f_x}'(x_0,y_0)]^2+[{f_y}'(x_0,y_0)]^2$

等号成立的条件就是两个向量的夹角为 0，也就是平行，也就是

$\frac{cos\theta}{{f_x}'(x_0,y_0)} = \frac{sin\theta}{{f_y}'(x_0,y_0)}$

也就是

$\frac{cos\theta}{sin\theta} = \frac{{f_x}'(x_0,y_0)}{{f_y}'(x_0,y_0)}$

也即使单位长度的增长量最大的方向 $\theta$ 为 $arctan\frac{{f_y}'(x_0,y_0)}{{f_x}'(x_0,y_0)}$

上面是我们从任一点出发，推导出来的函数值上升最大的方向！下面我们来看看梯度的定义：

设函数 $f(x,y)$ 在区域 D 内有连续一阶导数， $P_0(x_0,y_0) \in D$，称向量
${f_x}'(x_0,y_0)\vec{i} + {f_y}'(x_0,y_0)\vec{j}$

为函数 $f(x,y)$ 在点 $P_0(x_0,y_0)$ 处的梯度，记作 $\vec{grad}f(x_0,y_0)$。

OK，可以看出，梯度向量的方向和我们之前推导的方向是一致的，所以梯度的方向就是函数增长最大的方向！

1.2 牛顿法

$x_{n+1} = x_n-\frac{{f}'(x_n)}{{f}''(x_n)}$

解释一（导函数的切线迭代）：

无约束的优化问题：

$x^{*}=\underset{x}{min}f(x),x\in \mathbb{R}^n$

可以找极值点，令 ${f}'(x) = 0$ 求出 $x$

曲线 $g = {f}'(x)$ 在点 $(x_n,{f}'(x_n))$处切线的方程如下（点斜式）：
$y-{f}'(x_n) = {f}''(x_n)(x-x_n)$

当直线方程中的 $y = 0$ 时
$x = x_n-\frac{{f}'(x_n)}{{f}''(x_n)}$

也即
$x_{n+1} = x_n-\frac{{f}'(x_n)}{{f}''(x_n)}$

然后继续计算点 $(x_{n+1},{f}'(x_{n+1}))$ 的切线方程，令直线方程中的 $y = 0$ 得到 $x_{n+2}$

不断的迭代下去，如果 ${f}'(x)$ 达到了要求，就可以停止迭代了，eg， $<10^{-5}$

解释二（用抛物线迭代）：

如上图所示，可以在点 $x_n$ 处用二次函数拟合，然后更新到该二次函数的极值点，得到点 $x_{n+1}$

选择什么样的二次函数拟合比较合适呢？

下面先看看泰勒定理（任何可导函数，都可以写成幂函数的形式）

---

定义：设 $f(x)$ 在闭区间 $[a,b]$ 有 $n$ 阶连续的导数，在开区间 $(a,b)$ 内有直到 $n+1$阶导数， $x_0 \in[a,b]$， $x \in[a,b]$ 是任意两点，则至少存在一点 $\xi$ 介于 $x_0$ 和 $x$ 之间，使
$f(x) = f(x_0)+\frac{{f}'(x_0)}{1!}(x-x_0)+\frac{{f}''(x_0)}{2!}(x-x_0)^2+...+\frac{{f}^{(n)}(x_0)}{n!}(x-x_0)^n+R(n)$

其中 $R_n = \frac{{f}^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}$ 称为拉格朗日余项，整个公式称为具有拉格朗日余项的 $n$ 阶泰勒公式。

---

回到我们的问题上来， $f(x)$ 可以表示成如下形式：
$\begin{aligned} f(x) &= f(x_n)+\frac{{f}'(x_n)}{1!}(x-x_n)+\frac{{f}''(x_n)}{2!}(x-x_n)^2+... \\ &=\frac{{f}''(x_n)}{2!}x^2+[{f}'(x_n)-\frac{{f}''(x_n)}{2!}2x_n]x+f(x_n)-{f}'(x_n)x_n+\frac{{f}''(x_n)}{2!}x_n^2...\\ &=\frac{{f}''(x_n)}{2!}x^2+[{f}'(x_n)-{f}''(x_n)x_n]x+f(x_n)-{f}'(x_n)x_n+\frac{{f}''(x_n)}{2!}x_n^2... \end{aligned}$

此时我们就可以用上面的抛物线来近似 $f(x)$，抛物线的极值点的横坐标为对称轴 $x =-\frac{b}{2a}$，代入 $a$ 和 $b$ 的值：

$\begin{aligned} x &= -\frac{{f}'(x_n)-{f}''(x_n)x_n}{2\times\frac{{f}''(x_n)}{2!}} \\ & = \frac{{f}''(x_n)x_n-{f}'(x_n)}{{f}''(x_n)} \\ & = x_n-\frac{{f}'(x_n)}{{f}''(x_n)} \\ \end{aligned}$
也即
$x_{n+1} = x_n-\frac{{f}'(x_n)}{{f}''(x_n)}$

注意，如果 $f(x)$ 为二次函数，只用迭代一次就可以到极小值点 $x^*$

---

上面 $x$ 是一维的情况，如果 $x$ 扩充到 $m$ 维， $x^{(n)} = (x_1^{(n)},x_2^{(n)},...x_m^{(n)})$，那么

$\bigtriangledown f = \begin{bmatrix} \frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\\ ...\\ \frac{\partial f}{\partial x_m} \end{bmatrix}$

为 $f$ 的梯度向量，记为 $g$

$\bigtriangledown ^2f = \begin{bmatrix} \frac{\partial ^2f}{\partial x_1^2} & \frac{\partial ^2f}{\partial x_1 \partial x_2} & ... & \frac{\partial ^2f}{\partial x_1 \partial x_m}\\ \frac{\partial ^2f}{\partial x_2 \partial x_1} & \frac{\partial ^2f}{\partial x_2^2}& ... & \frac{\partial ^2f}{\partial x_2 \partial x_m}\\ ... & ... & ...& ...\\ \frac{\partial ^2f}{\partial x_m \partial x_1} & \frac{\partial ^2f}{\partial x_m \partial x_2} & ... & \frac{\partial ^2f}{\partial x_m^2} \end{bmatrix}$

为 Hesse 矩阵，即为 $H$

所以，牛顿法可以表示成如下形式：

$\begin{aligned} x^{(n+1)} &= x^{(n)}-\frac{g_n}{H_n}\\ & = x^{(n)}-H_n^{-1}g_n \end{aligned}$

图片来源于：牛顿法与拟牛顿法学习笔记（一）牛顿法

1.3 梯度下降法和牛顿法的比较

梯下降是一次收敛

$||x_{n+1}-x^*||<k||x_{n}-x^*||，k \in (0,1)$

牛顿法二次收敛
$||x_{n+1}-x^*||<k||x_{n}-x^*||^2，k \in (0,1)$

速度快，但也有缺陷要在比较接近最优点的时候才能收敛，否则可发散，这一点很好的弥补了梯度下降法步长不好的时候在最优点的时候震荡的问题.

1.4 阻尼牛顿法

图片来源于：牛顿法与拟牛顿法学习笔记（一）牛顿法

设置了步长 $\lambda$，每次迭代方向仍为 $d_k$，但每次迭代需沿此方向作一维搜索 line search

$\lambda_k = arg \underset{\lambda \in \mathbb{R}}{min}f(x_k+\lambda_k d_k)$

1.5 拟牛顿条件

参考 牛顿法与拟牛顿法学习笔记（二）拟牛顿条件

Hesse 矩阵可能没有逆，也可能比较难求，拟牛顿法提出，用不含二阶导数的矩阵 $U_k$ 替代牛顿法中的 $H_k^{-1}$，然后沿搜索方向 $-U_kg_k$ 做一维搜索。根据不同的 $U_k$ 构造方法有不同的拟牛顿法!

常见的拟牛顿法有

• DFP（ 牛顿法与拟牛顿法学习笔记（三）DFP 算法）
• BFGS（牛顿法与拟牛顿法学习笔记（四）BFGS 算法）
• L-BFGS（牛顿法与拟牛顿法学习笔记（五）L-BFGS 算法）

但是不能随便近似，需要理论的指导，拟牛顿条件就是近似需要满足的条件。

迭代 $k+1$ 次后得到 $x_{k+1}$，此时 $f(x)$ 在 $x_{k+1}$ 附近展开，取二阶近似：

$f(x) \approx f(x_{k+1})+\frac{\bigtriangledown f(x_{k+1})}{1!}(x-x_{k+1})+\frac{\bigtriangledown ^2f(x_{k+1})}{2!}(x-x_{k+1})^2$

两边同时求梯度：

$\bigtriangledown f(x) \approx \bigtriangledown f(x_{k+1})+\frac{\bigtriangledown ^2f(x_{k+1})}{1!}(x-x_{k+1})$

也即
$\bigtriangledown f(x) \approx g_{k+1}+H_{k+1}(x-x_{k+1})$

令 $x$ 为 $x_k$，则

$g_k \approx g_{k+1}+H_{k+1}(x_k-x_{k+1})$

$g_k - g_{k+1} \approx H_{k+1}(x_k-x_{k+1})$

或者

$x_k-x_{k+1}\approx H_{k+1}^{-1}(g_k - g_{k+1} )$

对 Hesse 矩阵做了约束，这就是拟牛顿条件

我们令 $B \approx H$， $D \approx H^{-1}$， $s_k = x_{k+1}-x_k$， $y_k = g_{k+1}-g_k$，则拟牛顿条件可以简化表示为

$y_k \approx B_{k+1}\cdot s_k$

或者

$s_k \approx D_{k+1}\cdot y_k$

2 有约束的最优化问题

2.1 等式约束

$x^{*}=\underset{x}{min}f(x),x\in \mathbb{R}^n \\ s.t. g(x)=0$

以二维为例子

图中圆圈为 $f(x,y)$ 的等高线，要求使函数值最小的点，而且点还必须满足 $g(x,y)=0$！最优的点一定是 $g(x,y)$ 与 $f(x,y)$ 相切的时候

如果相交， $f(x,y)=d$ 与 $g(x,y)=0$ 至少有两个交点，那么介于这两个交点之间的任何一个 $(x,y)$ 满足 $g(x,y)=0$ 时， $f(x,y)\leq d$，显然，还有使函数值更小的点！eg，上面的， $f(x,y)=d_2$ 与 $g(x,y)=0$

此时呢
$\left\{\begin{matrix} \bigtriangledown f(x,y) = -\lambda \bigtriangledown g(x,y) \\ g(x,y) = 0 \end{matrix}\right.$

整合一下：
$L(x,y,\lambda) = f(x,y) + \lambda g(x,y)$

这就是耳熟能详的拉格朗日函数！你会发现，两边同时求梯度，令梯度为 0，对 $\lambda$ 求偏导，令偏导为0，结果就是上面的式子

---

我们再回过头去看看拉格朗日乘数法

求函数 $f(x,y)$ 在条件 $g(x,y)=0$ 条件下的极值

解决此类问题的一般方法是拉格朗日乘数法：
先构造拉格朗日函数 $L(x,y,\lambda) = f(x,y) + \lambda g(x,y)$，然后解方程组

$\left\{\begin{matrix} \frac{\partial L}{\partial x} = \frac{\partial f}{\partial x}+ \lambda \frac{\partial g}{\partial x} = 0,\\ \frac{\partial L}{\partial y} = \frac{\partial f}{\partial y}+ \lambda \frac{\partial g}{\partial y} = 0,\\ \frac{\partial L}{\partial \lambda} = g(x,y)=0, \end{matrix}\right.$

所有满足此方程组的解 $(x,y,\lambda)$ 中 $(x,y)$ 是函数 $f(x,y)$ 在条件 $g(x,y)=0$ 下的可能的极值点。

---

和我们推导出来的没有差异（梯度就是偏导的构成的向量），哈哈，只是我们使用的时候和推导的逻辑是反过来，

推导的时候，先有求偏导的形式，然后才构造出来拉格朗日函数，
使用的时候，拉格朗日函数信手拈来，然后再求偏导，令偏导为 0！

2.2 不等式约束（KKT）

分为上面两种情况，
如果是第一种情况，原 $f(x,y)$ 的最优值包含在约束条件当中，也就是说约束无作用
如果是第二种情况，原 $f(x,y)$ 的最优值不包含在约束条件当中，这个时候约束起了作用，但等价于等式约束，也就是 $g(x,y) = 0$

整合一下
$\left\{\begin{matrix} L(x,y,\mu) = f(x,y) + \mu g(x,y)\\ \mu \geq 0\\ \mu g(x^*,y^*) = 0 \end{matrix}\right.$

当 $\mu = 0$， $g(x,y) \leq 0$

当 $\mu\geq 0$， $g(x,y) =0$

下面加上等式和不等式约束，看看完整的 KKT 条件的定义

截图自

非线性优化中的 KKT 条件该如何理解？ - 马同学的回答 - 知乎
https://www.zhihu.com/question/23311674/answer/468804362

---

我们也可以换一个角度来分析 KKT 条件

广义 Lagrangian 可以定义为：

$L(x,\lambda,\mu) =f(x) + \sum_i\lambda_ig^{(i)}(x) + \sum_j\mu_jh^{(j)}(x)$

带约束的优化问题等价为：

$\underset{x}{min}\ \underset{\lambda }{max}\ \underset{\mu,\mu \geq0}{max} \ L(x,\lambda ,\mu )$

如果 $h^{(j)}<0$， $\mu \geq 0$，求 min 的话， $\mu$ 只能为 0 了，要不然就是负无穷，没有意义了！

3 例题

求下列非线性规划问题的 K-T 点：

$min f(x) = 2x_1^2+2x_1x_2+x_2^2-10x_1-10x_2;$
$s.t.\left\{\begin{matrix} x_1^2+x_2^2 \leq 5,\\ 3x_{1}+x_{2}\leq 6. \end{matrix}\right.$

也就是 KKT 条件

解：

$h_1(x_1,x_2) = x_1^2+x_2^2 -5 \leq 0$

$h_2(x_1,x_2) = 3x_{1}+x_{2} - 6 \leq 0$

拉格朗日函数

$L(x_1,x_2,\mu_1,\mu_2) =f(x_1,x_2) + \mu_1h_1(x_1,x_2) + \mu_2h_2(x_1,x_2)$

$\bigtriangledown f(x_1,x_2) = \begin{bmatrix} 4x_1+2x_2-10\\ 2x_1+2x_2-10 \end{bmatrix}$

$\bigtriangledown h_1(x_1,x_2) = \begin{bmatrix} 2x_1\\ 2x_2 \end{bmatrix}$

$\bigtriangledown h_2(x_1,x_2) = \begin{bmatrix} 3\\ 1 \end{bmatrix}$

KKT 条件

$\left\{\begin{matrix} 4x_1+2x_2-10 + 2\mu_1x_1 + 3\mu_2 = 0\\ 2x_1+2x_2-10 + 2\mu_1x_2 + \mu_2 = 0\\ x_1^2+x_2^2 -5 \leq 0\\ 3x_{1}+x_{2} - 6 \leq 0\\ \mu_1 \geq 0\\ \mu_2 \geq 0\\ \mu_1(x_1^2+x_2^2 -5) = 0\\ \mu_2(3x_{1}+x_{2} - 6) = 0 \end{matrix}\right.$

这种题目，解无定法，观察得之（可以从如下情况考虑）

• 变量的对称性： $x_1 = -x_2$
• 特殊取值试探法： $\mu = 0$
• 将 $\frac{\partial L}{\partial x_1}$， $\frac{\partial L}{\partial x_2}$ 中的 $\mu$ 去掉，然后求出来结果代入到 $\frac{\partial L}{\partial \mu}$ 中

本题求解的最终结果为：

$\left\{\begin{matrix} x_1^* = 1\\ x_2^* = 2\\ \mu_1 = 1\\ \mu_2 = 0 \end{matrix}\right.$

也就是第一个约束 $h_1(x_1,x_2)$ 起了作用，第二个约束 $h_2(x_1,x_2)$ 没起作用！

我们把 $(x_1^*,x_2^*)$ 的结果代入 $h_1(x_1,x_2)$ 和 $h_2(x_1,x_2)$ 中一探究竟

$h_1(x_1^*,x_2^*) = 0 \\ h_2(x_1^*,x_2^*) = -1$

确实
$h_1$ 在边界上，起到了约束作用，对应的 $\mu_1 \geq 0$
$h_2$ 在约束的内部，没有起到约束作用，对应的 $\mu_2 = 0$