一些重要的求解约束优化的方法
将原问题替换为一系列子问题 , 在子问题中原本的约束被替换成加在目标函数上的项. 本章我们介绍属于此类的三种方法.
二次罚函数法the quadratic penalty method 是在目标函数上增加每个约束违反度平方的某个倍数. 这种方法比较简单、直观 . 尽管它有许多的缺陷 , 但实际中还是被经常使用 .非光滑精确罚函数法the nonsmooth exact penalty methods 是用一个 (而不是一系列)无约束问题替代原本的约束问题. 使用这种罚函数, 我们可以仅利用一次无约束极小化找到解, 但随之而来, 非光滑性可能会制造一些麻烦. 此类的常见罚函数比如
l
1
l_1
l 1 乘子法the methods of multipliers 或增广Lagrange函数法the augmented Lagrangian method 是另一种精确罚函数法, 其中显式估计了Lagrange乘子, 避免了二次罚函数带来的病态问题 .对数障碍函数法log-barrier method 使用对数项来防止迭代点过于接近可行域边界. 此法是非线性规划内点法的部分基础. 我们放在第十九章讲述.
考虑使用单一个 函数代替约束优化问题, 其中那个函数由以下组成:
约束优化问题的目标函数 , 加上
对每个约束的一个附加项 , 其在当前点违反约束时为正, 否则取0.
许多方法都会通过定义一系列这样的罚函数求解问题, 其中罚项乘上了一个正系数(惩罚因子). 此系数越大, 我们对违反约束的现象越不能容忍, 从而越强制罚函数的极小点靠近约束问题的可行域 .
此类最简单的罚函数为二次罚函数(又称Courant罚函数) , 其中的罚项记为约束违反度的平方. 我们先在等式约束问题下讨论这一方法.
min
x
f
(
x
)
,
s
u
b
j
e
c
t
 
t
o
 
c
i
(
x
)
=
0
,
i
∈
E
.
\min\limits_xf(x),\quad\mathrm{subject\,to\,}c_i(x)=0,\quad i\in\mathcal{E}.
x min f ( x ) , s u b j e c t t o c i ( x ) = 0 , i ∈ E .
Q
(
x
;
μ
)
=
d
e
f
f
(
x
)
+
μ
2
∑
i
∈
E
c
i
2
(
x
)
,
Q(x;\mu)\xlongequal{def}f(x)+\frac{\mu}{2}\sum_{i\in\mathcal{E}}c_i^2(x),
Q ( x ; μ ) d e f
f ( x ) + 2 μ i ∈ E ∑ c i 2 ( x ) ,
μ
>
0
\mu>0
μ > 0 惩罚因子(penalty parameter) . 当
μ
\mu
μ
∞
\infty
∞
{
μ
k
}
:
μ
↑
∞
,
k
→
∞
\{\mu_k\}:\mu\uparrow\infty,k\to\infty
{ μ k } : μ ↑ ∞ , k → ∞
k
k
k
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k )
x
k
x_k
x k
x
k
x_k
x k
x
k
x_k
x k
x
k
−
1
,
x
k
−
2
x_{k-1},x_{k-2}
x k − 1 , x k − 2 初始的迭代点 . 对于合适的
{
μ
k
}
\{\mu_k\}
{ μ k }
例1 考虑以下等式约束问题
min
x
1
+
x
2
,
s
u
b
j
e
c
t
 
t
o
 
x
1
2
+
x
2
2
−
2
=
0
,
\min x_1+x_2,\quad\mathrm{subject\,to\,}x_1^2+x_2^2-2=0,
min x 1 + x 2 , s u b j e c t t o x 1 2 + x 2 2 − 2 = 0 ,
(
−
1
,
−
1
)
T
(-1,-1)^T
( − 1 , − 1 ) T
Q
(
x
;
μ
)
=
x
1
+
x
2
+
μ
2
(
x
1
2
+
x
2
2
−
2
)
2
.
Q(x;\mu)=x_1+x_2+\frac{\mu}{2}(x_1^2+x_2^2-2)^2.
Q ( x ; μ ) = x 1 + x 2 + 2 μ ( x 1 2 + x 2 2 − 2 ) 2 .
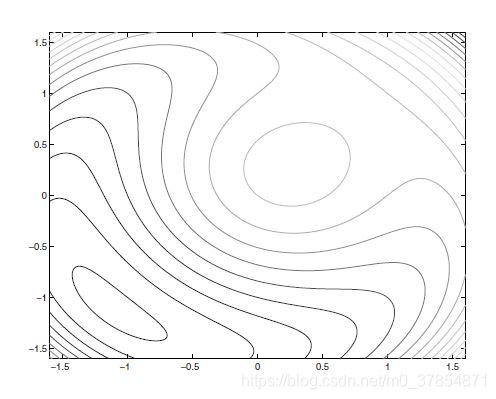
μ
=
1
\mu=1
μ = 1
Q
Q
Q
Q
Q
Q
(
−
1.1
,
−
1.1
)
T
(-1.1,-1.1)^T
( − 1 . 1 , − 1 . 1 ) T
(
0.3
,
0.3
)
T
(0.3,0.3)^T
( 0 . 3 , 0 . 3 ) T
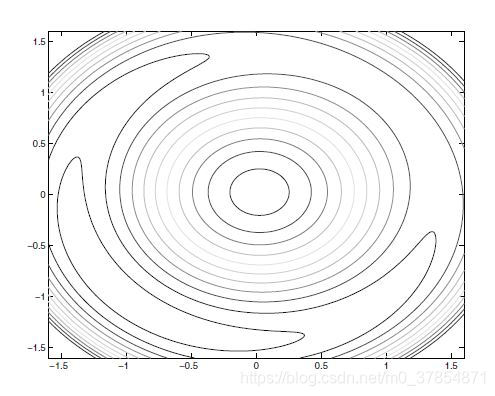
而下图则对应
μ
=
10
\mu=10
μ = 1 0
x
1
2
+
x
2
2
=
2
x_1^2+x_2^2=2
x 1 2 + x 2 2 = 2
Q
Q
Q
(
0
,
0
)
T
(0,0)^T
( 0 , 0 ) T
Q
Q
Q
∞
\infty
∞
但实际情形一般没有例1中那么良态. 对于一给定的
μ
\mu
μ
min
−
5
x
1
2
+
x
2
2
,
s
u
b
j
e
c
t
 
t
o
 
x
1
=
1
,
\min -5x_1^2+x_2^2,\quad\mathrm{subject\,to\,}x_1=1,
min − 5 x 1 2 + x 2 2 , s u b j e c t t o x 1 = 1 ,
(
1
,
0
)
T
(1,0)^T
( 1 , 0 ) T
对于一般的约束优化问题
min
x
f
(
x
)
,
s
u
b
j
e
c
t
 
t
o
 
c
i
(
x
)
=
0
,
i
∈
E
,
c
i
(
x
)
≥
0
,
i
∈
I
.
\min\limits_xf(x),\quad\mathrm{subject\,to\,}c_i(x)=0,i\in\mathcal{E},\quad c_i(x)\ge0,i\in\mathcal{I}.
x min f ( x ) , s u b j e c t t o c i ( x ) = 0 , i ∈ E , c i ( x ) ≥ 0 , i ∈ I .
Q
(
x
;
μ
)
=
d
e
f
f
(
x
)
+
μ
2
∑
i
∈
E
c
i
2
(
x
)
+
μ
2
∑
i
∈
I
(
[
c
i
(
x
)
]
−
)
2
,
Q(x;\mu)\xlongequal{def}f(x)+\frac{\mu}{2}\sum_{i\in\mathcal{E}}c_i^2(x)+\frac{\mu}{2}\sum_{i\in\mathcal{I}}\left([c_i(x)]^-\right)^2,
Q ( x ; μ ) d e f
f ( x ) + 2 μ i ∈ E ∑ c i 2 ( x ) + 2 μ i ∈ I ∑ ( [ c i ( x ) ] − ) 2 ,
[
y
]
−
=
max
(
−
y
,
0
)
[y]^-=\max(-y,0)
[ y ] − = max ( − y , 0 ) 此时
Q
Q
Q . 例如若有一个不等式约束为
x
1
≥
0
x_1\ge0
x 1 ≥ 0
min
(
0
,
x
1
)
2
\min(0,x_1)^2
min ( 0 , x 1 ) 2
Q
Q
Q
基于二次罚函数的一般算法框架如下.
框架1 (Quadratic Penalty Method)
μ
0
>
0
\mu_0>0
μ 0 > 0
{
τ
k
}
\{\tau_k\}
{ τ k }
τ
k
→
0
\tau_k\to0
τ k → 0
x
0
s
x_0^s
x 0 s
k
=
0
,
1
,
2
,
…
k=0,1,2,\ldots
k = 0 , 1 , 2 , …
\quad\quad
x
k
x_k
x k
Q
(
⋅
;
μ
k
)
Q(\cdot;\mu_k)
Q ( ⋅ ; μ k )
x
k
s
x_k^s
x k s
∥
∇
x
Q
(
x
;
μ
k
)
∥
≤
τ
k
\Vert\nabla_xQ(x;\mu_k)\Vert\le\tau_k
∥ ∇ x Q ( x ; μ k ) ∥ ≤ τ k
\quad\quad
\quad\quad\quad\quad
x
k
x_k
x k
\quad\quad
\quad\quad
μ
k
+
1
>
μ
k
\mu_{k+1}>\mu_k
μ k + 1 > μ k
\quad\quad
x
k
+
1
s
x_{k+1}^s
x k + 1 s
我们可以基于在每次迭代极小化罚函数的困难度自适应 地选取惩罚因子序列
{
μ
k
}
\{\mu_k\}
{ μ k }
当极小化
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k )
k
k
k
μ
k
\mu_k
μ k
μ
k
+
1
\mu_{k+1}
μ k + 1
μ
k
+
1
=
1.5
μ
k
\mu_{k+1}=1.5\mu_k
μ k + 1 = 1 . 5 μ k
若我们比较容易就能找到
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k )
μ
k
+
1
=
10
μ
k
\mu_{k+1}=10\mu_k
μ k + 1 = 1 0 μ k
框架1的收敛理论给予了非负序列
{
τ
k
}
\{\tau_k\}
{ τ k }
τ
k
→
0
\tau_k\to0
τ k → 0
正如之前讨论过的, 我们无法保证
∥
∇
x
Q
(
x
;
μ
k
)
∥
≤
τ
k
\Vert\nabla_xQ(x;\mu_k)\Vert\le\tau_k
∥ ∇ x Q ( x ; μ k ) ∥ ≤ τ k 当约束违反度下降不够快, 或者当迭代点趋向于发散时, 增大惩罚因子(或存储初始点)的防护措施 .
当只有等式约束时,
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k )
x
k
x_k
x k
μ
k
\mu_k
μ k
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k ) 条件数变大 ), 除非我们使用特殊的手段计算搜索方向.
一方面, Hessian阵
∇
x
x
2
Q
(
x
;
μ
k
)
\nabla_{xx}^2Q(x;\mu_k)
∇ x x 2 Q ( x ; μ k )
μ
k
\mu_k
μ k
在我们求解线性系统计算牛顿步时, 病态的
∇
x
x
2
Q
(
x
;
μ
k
)
\nabla_{xx}^2Q(x;\mu_k)
∇ x x 2 Q ( x ; μ k )
即使
x
x
x
Q
(
⋅
;
μ
k
)
Q(\cdot;\mu_k)
Q ( ⋅ ; μ k )
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k )
x
x
x
Q
Q
Q
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k )
x
k
+
1
s
x_{k+1}^s
x k + 1 s
x
k
+
1
s
=
x
k
x_{k+1}^s=x_k
x k + 1 s = x k
μ
k
+
1
\mu_{k+1}
μ k + 1
μ
k
\mu_k
μ k
我们在下面两个定理里介绍二次罚函数方法的一些收敛性质. 我们将讨论限制在等式约束问题.
对于第一个结果, 我们假设对每个
μ
k
\mu_k
μ k
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k )
定理1 设
x
k
x_k
x k
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k )
μ
k
↑
∞
\mu_k\uparrow\infty
μ k ↑ ∞
{
x
k
}
\{x_k\}
{ x k }
证明: 令
x
ˉ
\bar{x}
x ˉ
f
(
x
ˉ
)
≤
f
(
x
)
,
∀
x
:
c
i
(
x
)
=
0
,
i
∈
E
.
f(\bar{x})\le f(x),\quad\forall x:c_i(x)=0,i\in\mathcal{E}.
f ( x ˉ ) ≤ f ( x ) , ∀ x : c i ( x ) = 0 , i ∈ E .
k
k
k
x
k
x_k
x k
Q
(
⋅
;
μ
k
)
Q(\cdot;\mu_k)
Q ( ⋅ ; μ k )
Q
(
x
k
;
μ
k
)
≤
Q
(
x
ˉ
;
μ
k
)
Q(x_k;\mu_k)\le Q(\bar{x};\mu_k)
Q ( x k ; μ k ) ≤ Q ( x ˉ ; μ k )
f
(
x
k
)
+
μ
k
2
∑
i
∈
E
c
i
2
(
x
k
)
≤
f
(
x
ˉ
)
+
μ
k
2
∑
i
∈
E
c
i
2
(
x
ˉ
)
=
f
(
x
ˉ
)
.
f(x_k)+\frac{\mu_k}{2}\sum_{i\in\mathcal{E}}c_i^2(x_k)\le f(\bar{x})+\frac{\mu_k}{2}\sum_{i\in\mathcal{E}}c_i^2(\bar{x})=f(\bar{x}).
f ( x k ) + 2 μ k i ∈ E ∑ c i 2 ( x k ) ≤ f ( x ˉ ) + 2 μ k i ∈ E ∑ c i 2 ( x ˉ ) = f ( x ˉ ) .
∑
i
∈
E
c
i
2
(
x
k
)
≤
2
μ
k
[
f
(
x
ˉ
)
−
f
(
x
k
)
]
.
\sum_{i\in\mathcal{E}}c_i^2(x_k)\le\frac{2}{\mu_k}[f(\bar{x})-f(x_k)].
i ∈ E ∑ c i 2 ( x k ) ≤ μ k 2 [ f ( x ˉ ) − f ( x k ) ] .
x
∗
x^*
x ∗
{
x
k
}
\{x_k\}
{ x k }
{
1
,
2
,
…
,
n
,
…
}
\{1,2,\ldots,n,\ldots\}
{ 1 , 2 , … , n , … }
K
\mathcal{K}
K
lim
k
→
K
x
k
=
x
∗
.
\lim_{k\to\mathcal{K}}x_k=x^*.
k → K lim x k = x ∗ .
k
→
∞
,
k
∈
K
k\to\infty,k\in\mathcal{K}
k → ∞ , k ∈ K
∑
i
∈
E
c
i
2
(
x
∗
)
=
lim
k
∈
K
∑
i
∈
E
c
i
2
(
x
k
)
≤
lim
k
∈
K
2
μ
k
[
f
(
x
ˉ
)
−
f
(
x
k
)
]
=
0.
\sum_{i\in\mathcal{E}}c_i^2(x^*)=\lim_{k\in\mathcal{K}}\sum_{i\in\mathcal{E}}c_i^2(x_k)\le\lim_{k\in\mathcal{K}}\frac{2}{\mu_k}[f(\bar{x})-f(x_k)]=0.
i ∈ E ∑ c i 2 ( x ∗ ) = k ∈ K lim i ∈ E ∑ c i 2 ( x k ) ≤ k ∈ K lim μ k 2 [ f ( x ˉ ) − f ( x k ) ] = 0 .
c
i
(
x
∗
)
=
0
,
i
∈
E
c_i(x^*)=0,i\in\mathcal{E}
c i ( x ∗ ) = 0 , i ∈ E
x
∗
x^*
x ∗
f
(
x
∗
)
≤
f
(
x
∗
)
+
lim
k
∈
K
μ
k
2
∑
i
∈
E
c
i
2
(
x
k
)
≤
f
(
x
ˉ
)
.
f(x^*)\le f(x^*)+\lim_{k\in\mathcal{K}}\frac{\mu_k}{2}\sum_{i\in\mathcal{E}}c_i^2(x_k)\le f(\bar{x}).
f ( x ∗ ) ≤ f ( x ∗ ) + k ∈ K lim 2 μ k i ∈ E ∑ c i 2 ( x k ) ≤ f ( x ˉ ) .
x
∗
x^*
x ∗
x
ˉ
\bar{x}
x ˉ
x
∗
x^*
x ∗
此结论对带不等式的问题也成立. 但由于需要我们求每个子问题的全局极小点, 因此此性质一般并不能成立 . 下一结论则允许我们不精确(但精确度要提升)极小化
Q
(
⋅
;
μ
k
)
Q(\cdot;\mu_k)
Q ( ⋅ ; μ k )
{
x
k
}
\{x_k\}
{ x k }
−
μ
k
c
i
(
x
k
)
-\mu_kc_i(x_k)
− μ k c i ( x k )
λ
i
∗
\lambda_i^*
λ i ∗
为建立定理, 我们需乐观地 假设对所有
k
k
k
∥
∇
x
Q
(
x
;
μ
k
)
∥
≤
τ
k
\Vert\nabla_xQ(x;\mu_k)\Vert\le\tau_k
∥ ∇ x Q ( x ; μ k ) ∥ ≤ τ k
定理2 设框架1中的容忍限序列和惩罚因子序列满足
τ
k
→
0
,
μ
k
↑
∞
\tau_k\to0,\mu_k\uparrow\infty
τ k → 0 , μ k ↑ ∞
{
x
k
}
\{x_k\}
{ x k }
x
∗
x^*
x ∗
∥
c
(
x
)
∥
2
\Vert c(x)\Vert^2
∥ c ( x ) ∥ 2
x
∗
x^*
x ∗
∇
c
i
(
x
∗
)
\nabla c_i(x^*)
∇ c i ( x ∗ )
x
∗
x^*
x ∗
x
∗
x^*
x ∗
∀
K
:
lim
k
∈
K
x
k
=
x
∗
\forall\mathcal{K}:\lim_{k\in\mathcal{K}}x_k=x^*
∀ K : lim k ∈ K x k = x ∗
lim
k
∈
K
−
μ
k
c
i
(
x
k
)
=
λ
i
∗
,
∀
i
∈
E
,
\lim_{k\in\mathcal{K}}-\mu_kc_i(x_k)=\lambda_i^*,\quad\forall i\in\mathcal{E},
k ∈ K lim − μ k c i ( x k ) = λ i ∗ , ∀ i ∈ E ,
λ
∗
\lambda^*
λ ∗
证明: 对
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k )
∇
x
Q
(
x
k
;
μ
k
)
=
∇
f
(
x
k
)
+
∑
i
∈
E
μ
k
c
i
(
x
k
)
∇
c
i
(
x
k
)
,
\nabla_xQ(x_k;\mu_k)=\nabla f(x_k)+\sum_{i\in\mathcal{E}}\mu_kc_i(x_k)\nabla c_i(x_k),
∇ x Q ( x k ; μ k ) = ∇ f ( x k ) + i ∈ E ∑ μ k c i ( x k ) ∇ c i ( x k ) ,
∥
∇
f
(
x
k
)
+
∑
i
∈
E
μ
k
c
i
(
x
k
)
∇
c
i
(
x
k
)
∥
≤
τ
k
.
\left\Vert\nabla f(x_k)+\sum_{i\in\mathcal{E}}\mu_kc_i(x_k)\nabla c_i(x_k)\right\Vert\le\tau_k.
∥ ∥ ∥ ∥ ∥ ∇ f ( x k ) + i ∈ E ∑ μ k c i ( x k ) ∇ c i ( x k ) ∥ ∥ ∥ ∥ ∥ ≤ τ k .
∥
∑
i
∈
E
c
i
(
x
k
)
∇
c
i
(
x
k
)
∥
≤
1
μ
k
[
τ
k
+
∥
∇
f
(
x
k
)
∥
]
.
\left\Vert\sum_{i\in\mathcal{E}}c_i(x_k)\nabla c_i(x_k)\right\Vert\le\frac{1}{\mu_k}[\tau_k+\Vert\nabla f(x_k)\Vert].
∥ ∥ ∥ ∥ ∥ i ∈ E ∑ c i ( x k ) ∇ c i ( x k ) ∥ ∥ ∥ ∥ ∥ ≤ μ k 1 [ τ k + ∥ ∇ f ( x k ) ∥ ] .
x
∗
x^*
x ∗
K
\mathcal{K}
K
lim
k
∈
K
x
k
=
x
∗
\lim_{k\in\mathcal{K}}x_k=x^*
lim k ∈ K x k = x ∗
k
→
∞
,
k
∈
K
k\to\infty,k\in\mathcal{K}
k → ∞ , k ∈ K
∑
i
∈
E
c
i
(
x
∗
)
∇
c
i
(
x
∗
)
=
0.
\sum_{i\in\mathcal{E}}c_i(x^*)\nabla c_i(x^*)=0.
i ∈ E ∑ c i ( x ∗ ) ∇ c i ( x ∗ ) = 0 .
c
i
(
x
∗
)
≠
0
c_i(x^*)\ne0
c i ( x ∗ ) ̸ = 0
∇
c
i
(
x
∗
)
\nabla c_i(x^*)
∇ c i ( x ∗ )
x
∗
x^*
x ∗
∥
c
(
x
)
∥
2
\Vert c(x)\Vert^2
∥ c ( x ) ∥ 2
若
∇
c
i
(
x
∗
)
\nabla c_i(x^*)
∇ c i ( x ∗ )
c
i
(
x
∗
)
=
0
,
∀
i
∈
E
c_i(x^*)=0,\forall i\in\mathcal{E}
c i ( x ∗ ) = 0 , ∀ i ∈ E
x
∗
x^*
x ∗
A
A
A
−
μ
k
c
(
x
k
)
-\mu_kc(x_k)
− μ k c ( x k )
λ
k
\lambda_k
λ k
A
(
x
k
)
T
λ
k
=
∇
f
(
x
k
)
−
∇
x
Q
(
x
k
;
μ
k
)
,
∥
∇
x
Q
(
x
k
;
μ
k
)
∥
≤
τ
k
.
A(x_k)^T\lambda_k=\nabla f(x_k)-\nabla_xQ(x_k;\mu_k),\quad\Vert\nabla_xQ(x_k;\mu_k)\Vert\le\tau_k.
A ( x k ) T λ k = ∇ f ( x k ) − ∇ x Q ( x k ; μ k ) , ∥ ∇ x Q ( x k ; μ k ) ∥ ≤ τ k .
k
∈
K
k\in\mathcal{K}
k ∈ K
A
(
x
k
)
A(x_k)
A ( x k )
A
(
x
k
)
A
(
x
k
)
T
A(x_k)A(x_k)^T
A ( x k ) A ( x k ) T
A
(
x
k
)
A(x_k)
A ( x k )
λ
k
=
[
A
(
x
k
)
A
(
x
k
)
T
]
−
1
A
(
x
k
)
[
∇
f
(
x
k
)
−
∇
x
Q
(
x
k
;
μ
k
)
]
.
\lambda_k=\left[A(x_k)A(x_k)^T\right]^{-1}A(x_k)[\nabla f(x_k)-\nabla_xQ(x_k;\mu_k)].
λ k = [ A ( x k ) A ( x k ) T ] − 1 A ( x k ) [ ∇ f ( x k ) − ∇ x Q ( x k ; μ k ) ] .
k
→
∞
,
k
∈
K
k\to\infty,k\in\mathcal{K}
k → ∞ , k ∈ K
lim
k
∈
K
λ
k
=
λ
∗
=
[
A
(
x
∗
)
A
(
x
∗
)
T
]
−
1
A
(
x
∗
)
∇
f
(
x
∗
)
.
\lim_{k\in\mathcal{K}}\lambda_k=\lambda^*=\left[A(x^*)A(x^*)^T\right]^{-1}A(x^*)\nabla f(x^*).
k ∈ K lim λ k = λ ∗ = [ A ( x ∗ ) A ( x ∗ ) T ] − 1 A ( x ∗ ) ∇ f ( x ∗ ) .
∇
f
(
x
∗
)
−
A
(
x
∗
)
T
λ
∗
=
0
,
\nabla f(x^*)-A(x^*)^T\lambda^*=0,
∇ f ( x ∗ ) − A ( x ∗ ) T λ ∗ = 0 ,
λ
∗
\lambda^*
λ ∗
x
∗
x^*
x ∗
λ
∗
\lambda^*
λ ∗
需重复强调的是, 若聚点
x
∗
x^*
x ∗
∥
c
(
x
)
∥
2
\Vert c(x)\Vert^2
∥ c ( x ) ∥ 2 第十一章 中讨论非线性方程组的情形. 在原问题不可行时, 我们往往可以观察到二次罚函数算法收敛于
∥
c
(
x
)
∥
2
\Vert c(x)\Vert^2
∥ c ( x ) ∥ 2
若考虑不等式约束, 则
x
∗
x^*
x ∗
∥
[
c
(
x
)
]
−
∥
2
\Vert [c(x)]^-\Vert^2
∥ [ c ( x ) ] − ∥ 2
[
c
(
x
)
]
−
[c(x)]^-
[ c ( x ) ] −
[
c
(
x
)
]
i
−
=
{
c
i
(
x
)
,
i
∈
E
,
[
c
i
(
x
)
]
−
,
i
∈
I
.
[c(x)]_i^-=\left\{\begin{array}{ll}c_i(x), & i\in\mathcal{E},\\ [c_i(x)]^-, & i\in\mathcal{I}.\end{array}\right.
[ c ( x ) ] i − = { c i ( x ) , [ c i ( x ) ] − , i ∈ E , i ∈ I .
我们现在来验证Hessian阵
∇
x
x
2
Q
(
x
;
μ
k
)
\nabla^2_{xx}Q(x;\mu_k)
∇ x x 2 Q ( x ; μ k )
这里的Hessian阵为
∇
x
x
2
Q
(
x
;
μ
k
)
=
∇
2
f
(
x
)
+
∑
i
∈
E
μ
k
c
i
(
x
)
∇
2
c
i
(
x
)
+
μ
k
A
(
x
)
T
A
(
x
)
.
\nabla^2_{xx}Q(x;\mu_k)=\nabla^2f(x)+\sum_{i\in\mathcal{E}}\mu_kc_i(x)\nabla^2c_i(x)+\mu_kA(x)^TA(x).
∇ x x 2 Q ( x ; μ k ) = ∇ 2 f ( x ) + i ∈ E ∑ μ k c i ( x ) ∇ 2 c i ( x ) + μ k A ( x ) T A ( x ) .
x
x
x
Q
(
⋅
;
μ
k
)
Q(\cdot;\mu_k)
Q ( ⋅ ; μ k )
∇
x
x
2
Q
(
x
;
μ
k
)
≈
∇
x
x
2
L
(
x
,
λ
∗
)
+
μ
k
A
(
x
)
T
A
(
x
)
.
\nabla^2_{xx}Q(x;\mu_k)\approx\nabla^2_{xx}\mathcal{L}(x,\lambda^*)+\mu_kA(x)^TA(x).
∇ x x 2 Q ( x ; μ k ) ≈ ∇ x x 2 L ( x , λ ∗ ) + μ k A ( x ) T A ( x ) .
∇
x
x
2
Q
(
x
;
μ
k
)
\nabla^2_{xx}Q(x;\mu_k)
∇ x x 2 Q ( x ; μ k )
(Lagrange项)独立于
μ
k
\mu_k
μ k
秩为
∣
E
∣
|\mathcal{E}|
∣ E ∣
μ
k
\mu_k
μ k
由于约束的数量
∣
E
∣
|\mathcal{E}|
∣ E ∣
n
n
n 某些特征值会趋近常数, 而其他的则与
μ
k
\mu_k
μ k . 因
μ
k
→
∞
\mu_k\to\infty
μ k → ∞
∇
x
x
2
Q
(
x
;
μ
k
)
\nabla^2_{xx}Q(x;\mu_k)
∇ x x 2 Q ( x ; μ k )
Hessian病态的一个后果是, 以下牛顿步的计算可能会不够精确:
∇
x
x
2
Q
(
x
;
μ
k
)
p
=
−
∇
x
Q
(
x
;
μ
k
)
.
\nabla^2_{xx}Q(x;\mu_k)p=-\nabla_xQ(x;\mu_k).
∇ x x 2 Q ( x ; μ k ) p = − ∇ x Q ( x ; μ k ) .
p
p
p
不过, 我们可以重构 以上牛顿方程以避免病态. 引入一个新的变量
ζ
:
=
μ
A
(
x
)
p
\zeta:=\mu A(x)p
ζ : = μ A ( x ) p
p
p
p
[
∇
2
f
(
x
)
+
∑
i
∈
E
μ
k
c
i
(
x
)
∇
2
c
i
(
x
)
A
(
x
)
T
A
(
x
)
−
(
1
/
μ
k
)
I
]
[
p
ζ
]
=
[
−
∇
x
Q
(
x
;
μ
k
)
0
]
.
\begin{bmatrix}\nabla^2f(x)+\sum\limits_{i\in\mathcal{E}}\mu_kc_i(x)\nabla^2c_i(x) & A(x)^T\\A(x) & -(1/\mu_k)I\end{bmatrix}\begin{bmatrix}p\\\zeta\end{bmatrix}=\begin{bmatrix}-\nabla_xQ(x;\mu_k)\\0\end{bmatrix}.
[ ∇ 2 f ( x ) + i ∈ E ∑ μ k c i ( x ) ∇ 2 c i ( x ) A ( x ) A ( x ) T − ( 1 / μ k ) I ] [ p ζ ] = [ − ∇ x Q ( x ; μ k ) 0 ] .
x
x
x
x
∗
x^*
x ∗
μ
k
\mu_k
μ k
μ
k
→
∞
\mu_k\to\infty
μ k → ∞
[
∇
x
x
2
L
(
x
,
λ
∗
)
A
(
x
)
T
A
(
x
)
O
]
,
\begin{bmatrix}\nabla^2_{xx}\mathcal{L}(x,\lambda^*) & A(x)^T\\A(x) & O\end{bmatrix},
[ ∇ x x 2 L ( x , λ ∗ ) A ( x ) A ( x ) T O ] ,
∇
x
x
2
L
(
x
,
λ
∗
)
\nabla^2_{xx}\mathcal{L}(x,\lambda^*)
∇ x x 2 L ( x , λ ∗ )
[
∇
x
x
2
L
(
x
,
λ
∗
)
A
(
x
)
T
A
(
x
)
O
]
∼
[
∇
x
x
2
L
(
x
,
λ
∗
)
A
(
x
)
T
O
−
A
(
x
)
[
∇
x
x
2
L
(
x
,
λ
∗
)
]
−
1
A
(
x
)
T
]
,
\begin{bmatrix}\nabla^2_{xx}\mathcal{L}(x,\lambda^*) & A(x)^T\\A(x) & O\end{bmatrix}\sim\begin{bmatrix}\nabla^2_{xx}\mathcal{L}(x,\lambda^*) & A(x)^T\\O & -A(x)\left[\nabla^2_{xx}\mathcal{L}(x,\lambda^*)\right]^{-1}A(x)^T\end{bmatrix},
[ ∇ x x 2 L ( x , λ ∗ ) A ( x ) A ( x ) T O ] ∼ [ ∇ x x 2 L ( x , λ ∗ ) O A ( x ) T − A ( x ) [ ∇ x x 2 L ( x , λ ∗ ) ] − 1 A ( x ) T ] , 良态重构(well conditioned reformulation) . 不过, 由于
∇
2
f
(
x
)
+
∑
i
∈
E
μ
k
c
i
(
x
)
∇
2
c
i
(
x
)
\nabla^2f(x)+\sum_{i\in\mathcal{E}}\mu_kc_i(x)\nabla^2c_i(x)
∇ 2 f ( x ) + ∑ i ∈ E μ k c i ( x ) ∇ 2 c i ( x )
∇
x
x
2
L
(
x
,
λ
∗
)
\nabla_{xx}^2\mathcal{L}(x,\lambda^*)
∇ x x 2 L ( x , λ ∗ )
μ
k
c
i
(
x
)
\mu_kc_i(x)
μ k c i ( x )
−
λ
i
∗
-\lambda_i^*
− λ i ∗
p
p
p
Q
(
⋅
;
μ
k
)
Q(\cdot;\mu_k)
Q ( ⋅ ; μ k )
如果要通过求解重构的问题计算迭代步, 我们需要求解一个
n
+
∣
E
∣
n+|\mathcal{E}|
n + ∣ E ∣
n
n
n
当
μ
k
\mu_k
μ k SQP迭代步的正则化 , 其中的
−
(
1
/
μ
k
)
I
-(1/\mu_k)I
− ( 1 / μ k ) I
A
(
x
)
A(x)
A ( x )
当
μ
k
\mu_k
μ k 不能较好地满足约束的线性化 . 我们是不希望这种情况发生的, 因为这样一来迭代步就不能朝着可行性改进多少, 从而全局表现不够高效.
若
{
μ
k
}
\{\mu_k\}
{ μ k } 丧失线性化满足时获得超线性收敛速度的机会 . 具体讨论可见下一章.
总之, 重构系统可以视作无约束极小在二次惩罚函数
Q
(
⋅
;
μ
k
)
Q(\cdot;\mu_k)
Q ( ⋅ ; μ k )
有些罚函数是精确的(exact) , 即对于特定的惩罚因子, 仅做一次极小化即可得到非线性规划问题的精确解. 这一性质是很吸引人的, 因为它使得罚函数方法不依赖于惩罚因子的更新策略 . 第1节介绍的二次罚函数并不是精确的, 这是因为对任何
μ
\mu
μ
l
1
l_1
l 1
ϕ
1
(
x
;
μ
)
=
f
(
x
)
+
μ
∑
i
∈
E
∣
c
i
(
x
)
∣
+
μ
∑
i
∈
I
[
c
i
(
x
)
]
−
.
\phi_1(x;\mu)=f(x)+\mu\sum_{i\in\mathcal{E}}|c_i(x)|+\mu\sum_{i\in\mathcal{I}}[c_i(x)]^-.
ϕ 1 ( x ; μ ) = f ( x ) + μ i ∈ E ∑ ∣ c i ( x ) ∣ + μ i ∈ I ∑ [ c i ( x ) ] − .
μ
\mu
μ
l
1
l_1
l 1
ϕ
1
(
x
;
μ
)
\phi_1(x;\mu)
ϕ 1 ( x ; μ )
x
x
x
下面的定理揭示了
l
1
l_1
l 1
定理3 设
x
∗
x^*
x ∗
λ
i
∗
,
i
∈
E
∪
I
\lambda_i^*,i\in\mathcal{E}\cup\mathcal{I}
λ i ∗ , i ∈ E ∪ I
x
∗
x^*
x ∗
ϕ
1
(
x
;
μ
)
,
∀
μ
>
μ
∗
\phi_1(x;\mu),\forall\mu>\mu^*
ϕ 1 ( x ; μ ) , ∀ μ > μ ∗
μ
∗
=
∥
λ
∗
∥
∞
=
max
i
∈
E
∪
I
∣
λ
i
∗
∣
.
\mu^*=\Vert\lambda^*\Vert_{\infty}=\max_{i\in\mathcal{E}\cup\mathcal{I}}|\lambda_i^*|.
μ ∗ = ∥ λ ∗ ∥ ∞ = i ∈ E ∪ I max ∣ λ i ∗ ∣ .
x
∗
x^*
x ∗
μ
>
μ
∗
\mu>\mu^*
μ > μ ∗
x
∗
x^*
x ∗
ϕ
1
(
x
;
μ
)
\phi_1(x;\mu)
ϕ 1 ( x ; μ )
证明可见 Han S P和Mangasarian O L的定理4.4.
粗略地说, 在非线性规划的解
x
∗
x^*
x ∗
ϕ
1
(
x
∗
;
μ
)
=
f
(
x
∗
)
\phi_1(x^*;\mu)=f(x^*)
ϕ 1 ( x ∗ ; μ ) = f ( x ∗ )
ϕ
(
⋅
;
μ
)
\phi(\cdot;\mu)
ϕ ( ⋅ ; μ )
x
∗
x^*
x ∗
例2 考虑如下单变量问题:
min
x
,
s
u
b
j
e
c
t
 
t
o
 
x
≥
1
,
\min x,\quad\mathrm{subject\,to\,}x\ge1,
min x , s u b j e c t t o x ≥ 1 ,
x
∗
=
1
x^*=1
x ∗ = 1
ϕ
1
(
x
;
μ
)
=
x
+
μ
[
x
−
1
]
−
=
{
(
1
−
μ
)
x
+
μ
,
x
≤
1
,
x
x
>
1.
\phi_1(x;\mu)=x+\mu[x-1]^-=\left\{\begin{array}{ll}(1-\mu)x+\mu, & x\le1,\\x & x>1.\end{array}\right.
ϕ 1 ( x ; μ ) = x + μ [ x − 1 ] − = { ( 1 − μ ) x + μ , x x ≤ 1 , x > 1 .
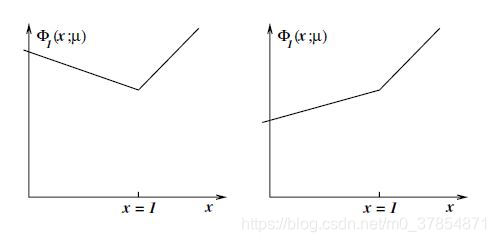
μ
>
1
\mu>1
μ > 1
x
∗
=
1
x^*=1
x ∗ = 1
μ
<
1
\mu<1
μ < 1
由于罚函数法通过直接极小化罚函数起作用, 所以我们需要刻画
ϕ
1
\phi_1
ϕ 1
ϕ
1
\phi_1
ϕ 1 方向导数
D
(
ϕ
1
(
x
;
μ
)
;
p
)
D(\phi_1(x;\mu);p)
D ( ϕ 1 ( x ; μ ) ; p )
定义1 一点
x
^
∈
R
n
\hat{x}\in\mathbb{R}^n
x ^ ∈ R n
ϕ
1
(
x
;
μ
)
\phi_1(x;\mu)
ϕ 1 ( x ; μ )
D
(
ϕ
1
(
x
^
;
μ
)
;
p
)
≥
0
,
∀
p
∈
R
n
.
D(\phi_1(\hat{x};\mu);p)\ge0,\quad\forall p\in\mathbb{R}^n.
D ( ϕ 1 ( x ^ ; μ ) ; p ) ≥ 0 , ∀ p ∈ R n .
x
^
\hat{x}
x ^ 不可行度量(the measure of infeasibility)
h
(
x
)
=
∑
i
∈
E
∣
c
i
(
x
)
∣
+
∑
i
∈
I
[
c
i
(
x
)
]
−
h(x)=\sum_{i\in\mathcal{E}}|c_i(x)|+\sum_{i\in\mathcal{I}}[c_i(x)]^-
h ( x ) = i ∈ E ∑ ∣ c i ( x ) ∣ + i ∈ I ∑ [ c i ( x ) ] −
D
(
h
(
x
^
)
;
p
)
≥
0
,
∀
p
∈
R
n
D(h(\hat{x});p)\ge0,\forall p\in\mathbb{R}^n
D ( h ( x ^ ) ; p ) ≥ 0 , ∀ p ∈ R n
h
h
h 不可行稳定点(infeasible stationary point) .
对于例2中的函数, 我们在
x
∗
=
1
x^*=1
x ∗ = 1
D
(
ϕ
1
(
x
∗
;
μ
)
;
p
)
=
{
p
,
p
≥
0
,
(
1
−
μ
)
p
,
p
<
0.
D(\phi_1(x^*;\mu);p)=\left\{\begin{array}{ll}p, & p\ge0,\\(1-\mu)p, & p<0.\end{array}\right.
D ( ϕ 1 ( x ∗ ; μ ) ; p ) = { p , ( 1 − μ ) p , p ≥ 0 , p < 0 .
μ
>
1
\mu>1
μ > 1
D
(
ϕ
1
(
x
∗
;
μ
)
;
p
)
≥
0
,
∀
p
∈
R
D(\phi_1(x^*;\mu);p)\ge0,\forall p\in\mathbb{R}
D ( ϕ 1 ( x ∗ ; μ ) ; p ) ≥ 0 , ∀ p ∈ R
下面的结论则在一定程度上弥补了定理3的不足, 即证明了反方向: 在一定条件下,
ϕ
1
(
x
;
μ
)
\phi_1(x;\mu)
ϕ 1 ( x ; μ )
定理4 设
x
^
\hat{x}
x ^
ϕ
1
(
x
;
μ
)
,
∀
μ
>
μ
^
>
0
\phi_1(x;\mu),\forall\mu>\hat{\mu}>0
ϕ 1 ( x ; μ ) , ∀ μ > μ ^ > 0
x
^
\hat{x}
x ^
证明: 若
x
^
\hat{x}
x ^
D
(
ϕ
1
(
x
^
;
μ
)
;
p
)
=
∇
f
(
x
^
)
T
p
+
μ
∑
i
∈
E
∣
∇
c
i
(
x
^
)
T
p
∣
+
μ
∑
i
∈
I
∩
A
(
x
^
)
[
∇
c
i
(
x
^
)
T
p
]
−
,
?
?
?
D(\phi_1(\hat{x};\mu);p)=\nabla f(\hat{x})^Tp+\mu\sum_{i\in\mathcal{E}}\left|\nabla c_i(\hat{x})^Tp\right|+\mu\sum_{i\in\mathcal{I}\cap\mathcal{A}(\hat{x})}\left[\nabla c_i(\hat{x})^Tp\right]^-,???
D ( ϕ 1 ( x ^ ; μ ) ; p ) = ∇ f ( x ^ ) T p + μ i ∈ E ∑ ∣ ∣ ∇ c i ( x ^ ) T p ∣ ∣ + μ i ∈ I ∩ A ( x ^ ) ∑ [ ∇ c i ( x ^ ) T p ] − , ? ? ?
A
(
x
^
)
\mathcal{A}(\hat{x})
A ( x ^ )
x
^
\hat{x}
x ^
F
(
x
^
)
\mathcal{F}(\hat{x})
F ( x ^ )
p
p
p
F
(
x
^
)
\mathcal{F}(\hat{x})
F ( x ^ )
∣
∇
c
i
(
x
^
)
T
p
∣
+
∑
i
∈
I
∩
A
(
x
^
)
[
∇
c
i
(
x
^
)
T
p
]
−
=
0
,
\left|\nabla c_i(\hat{x})^Tp\right|+\sum_{i\in\mathcal{I}\cap\mathcal{A}(\hat{x})}\left[\nabla c_i(\hat{x})^Tp\right]^-=0,
∣ ∣ ∇ c i ( x ^ ) T p ∣ ∣ + i ∈ I ∩ A ( x ^ ) ∑ [ ∇ c i ( x ^ ) T p ] − = 0 ,
0
≤
D
(
ϕ
1
(
x
^
;
μ
)
;
p
)
=
∇
f
(
x
^
)
T
p
,
∀
p
∈
F
(
x
^
)
.
0\le D(\phi_1(\hat{x};\mu);p)=\nabla f(\hat{x})^Tp,\quad\forall p\in\mathcal{F}(\hat{x}).
0 ≤ D ( ϕ 1 ( x ^ ; μ ) ; p ) = ∇ f ( x ^ ) T p , ∀ p ∈ F ( x ^ ) .
λ
^
i
:
λ
^
i
≥
0
,
i
∈
I
∩
A
(
x
^
)
\hat{\lambda}_i:\hat{\lambda}_i\ge0,i\in\mathcal{I}\cap\mathcal{A}(\hat{x})
λ ^ i : λ ^ i ≥ 0 , i ∈ I ∩ A ( x ^ )
∇
f
(
x
^
)
=
∑
i
∈
A
(
x
^
)
λ
^
i
∇
c
i
(
x
^
)
.
\nabla f(\hat{x})=\sum_{i\in\mathcal{A}(\hat{x})}\hat{\lambda}_i\nabla c_i(\hat{x}).
∇ f ( x ^ ) = i ∈ A ( x ^ ) ∑ λ ^ i ∇ c i ( x ^ ) .
x
^
\hat{x}
x ^
若
x
^
\hat{x}
x ^
p
p
p
D
(
h
(
x
^
)
;
p
)
<
0
D(h(\hat{x});p)<0
D ( h ( x ^ ) ; p ) < 0
0
≤
D
(
ϕ
1
(
x
^
;
μ
)
;
p
)
=
∇
f
(
x
^
)
T
p
+
μ
D
(
h
(
x
^
)
;
p
)
,
∀
μ
充
分
大
,
0\le D(\phi_1(\hat{x};\mu);p)=\nabla f(\hat{x})^Tp+\mu D(h(\hat{x});p),\forall\mu充分大,
0 ≤ D ( ϕ 1 ( x ^ ; μ ) ; p ) = ∇ f ( x ^ ) T p + μ D ( h ( x ^ ) ; p ) , ∀ μ 充 分 大 ,
∇
f
(
x
^
)
T
p
→
∞
\nabla f(\hat{x})^Tp\to\infty
∇ f ( x ^ ) T p → ∞
例3 再考虑例1中的问题, 这里使用
l
1
l_1
l 1
ϕ
1
(
x
;
μ
)
=
x
1
+
x
2
+
μ
∣
x
1
2
+
x
2
2
−
2
∣
.
\phi_1(x;\mu)=x_1+x_2+\mu|x_1^2+x_2^2-2|.
ϕ 1 ( x ; μ ) = x 1 + x 2 + μ ∣ x 1 2 + x 2 2 − 2 ∣ .
ϕ
(
x
;
2
)
\phi(x;2)
ϕ ( x ; 2 )
x
∗
=
(
−
1
,
−
1
)
T
x^*=(-1,-1)^T
x ∗ = ( − 1 , − 1 ) T
事实上由定理3, 我们知道对于所有的
μ
>
∣
λ
∗
∣
=
0.5
\mu>|\lambda^*|=0.5
μ > ∣ λ ∗ ∣ = 0 . 5
ϕ
1
(
x
;
μ
)
\phi_1(x;\mu)
ϕ 1 ( x ; μ )
x
∗
x^*
x ∗
l
1
l_1
l 1
这些结论为基于
l
1
l_1
l 1
框架2 (Classical
l
1
l_1
l 1
μ
0
>
0
\mu_0>0
μ 0 > 0
τ
>
0
\tau>0
τ > 0
x
0
s
x_0^s
x 0 s
k
=
0
,
1
,
2
,
…
k=0,1,2,\ldots
k = 0 , 1 , 2 , …
\quad\quad
x
k
x_k
x k
ϕ
1
(
x
;
μ
k
)
\phi_1(x;\mu_k)
ϕ 1 ( x ; μ k )
x
k
s
x_k^s
x k s
\quad\quad
h
(
x
k
)
≤
τ
h(x_k)\le\tau
h ( x k ) ≤ τ
\quad\quad\quad\quad
x
k
x_k
x k
\quad\quad
\quad\quad
μ
k
+
1
>
μ
k
\mu_{k+1}>\mu_k
μ k + 1 > μ k
\quad\quad
x
k
+
1
s
x_{k+1}^s
x k + 1 s
这其中对于
ϕ
1
(
x
;
μ
k
)
\phi_1(x;\mu_k)
ϕ 1 ( x ; μ k ) 若使用
ϕ
1
(
x
;
μ
k
)
\phi_1(x;\mu_k)
ϕ 1 ( x ; μ k ) , 事情就变得好理解多了. 我们将在下一小节介绍, 这有点类似于逐步二次规划算法.
更新惩罚因子
μ
k
\mu_k
μ k
μ
0
\mu_0
μ 0
x
∗
x^*
x ∗
ϕ
1
(
x
;
μ
k
)
\phi_1(x;\mu_k)
ϕ 1 ( x ; μ k )
x
k
s
x_k^s
x k s
μ
k
\mu_k
μ k
l
1
l_1
l 1 如前所述,
ϕ
1
(
x
;
μ
)
\phi_1(x;\mu)
ϕ 1 ( x ; μ )
x
:
c
i
(
x
)
=
0
,
∃
i
∈
E
∪
I
x:c_i(x)=0,\exists i\in\mathcal{E}\cup\mathcal{I}
x : c i ( x ) = 0 , ∃ i ∈ E ∪ I
ϕ
1
(
x
;
μ
)
\phi_1(x;\mu)
ϕ 1 ( x ; μ )
c
i
c_i
c i
f
f
f
q
(
p
;
μ
)
=
f
(
x
)
+
∇
f
(
x
)
T
p
+
1
2
p
T
W
p
+
μ
∑
i
∈
E
∣
c
i
(
x
)
+
∇
c
i
(
x
)
T
p
∣
+
μ
∑
i
∈
I
[
c
i
(
x
)
+
∇
c
i
(
x
)
T
p
]
−
,
q(p;\mu)=f(x)+\nabla f(x)^Tp+\frac{1}{2}p^TWp+\mu\sum_{i\in\mathcal{E}}|c_i(x)+\nabla c_i(x)^Tp|+\mu\sum_{i\in\mathcal{I}}[c_i(x)+\nabla c_i(x)^Tp]^-,
q ( p ; μ ) = f ( x ) + ∇ f ( x ) T p + 2 1 p T W p + μ i ∈ E ∑ ∣ c i ( x ) + ∇ c i ( x ) T p ∣ + μ i ∈ I ∑ [ c i ( x ) + ∇ c i ( x ) T p ] − ,
W
W
W
f
f
f
c
i
,
i
∈
E
∪
I
c_i,i\in\mathcal{E}\cup\mathcal{I}
c i , i ∈ E ∪ I
q
(
p
;
μ
)
q(p;\mu)
q ( p ; μ )
min
p
,
r
,
s
,
t
f
(
x
)
+
1
2
p
T
W
p
+
∇
f
(
x
)
T
p
+
μ
∑
i
∈
E
(
r
i
+
s
i
)
+
μ
∑
i
∈
I
t
i
s
u
b
j
e
c
t
 
t
o
∇
c
i
(
x
)
T
p
+
c
i
(
x
)
=
r
i
−
s
i
,
i
∈
E
,
∇
c
i
(
x
)
T
p
+
c
i
(
x
)
≥
−
t
i
,
i
∈
I
,
r
,
s
,
t
≥
0.
\begin{array}{rl}\min\limits_{p,r,s,t} & f(x)+\frac{1}{2}p^TWp+\nabla f(x)^Tp+\mu\sum\limits_{i\in\mathcal{E}}(r_i+s_i)+\mu\sum\limits_{i\in\mathcal{I}}t_i\\\mathrm{subject\,to} & \nabla c_i(x)^Tp+c_i(x)=r_i-s_i,\quad i\in\mathcal{E},\\& \nabla c_i(x)^Tp+c_i(x)\ge-t_i,\quad i\in\mathcal{I},\\ & r,s,t\ge0.\end{array}
p , r , s , t min s u b j e c t t o f ( x ) + 2 1 p T W p + ∇ f ( x ) T p + μ i ∈ E ∑ ( r i + s i ) + μ i ∈ I ∑ t i ∇ c i ( x ) T p + c i ( x ) = r i − s i , i ∈ E , ∇ c i ( x ) T p + c i ( x ) ≥ − t i , i ∈ I , r , s , t ≥ 0 . 标准的二次规划求解器 求解. 即使再添加一个盒型(box-shaped)信赖域约束
∥
p
∥
∞
≤
Δ
\Vert p\Vert_{\infty}\le\Delta
∥ p ∥ ∞ ≤ Δ
ϕ
1
\phi_1
ϕ 1
选取和更新惩罚因子
μ
k
\mu_k
μ k
μ
k
>
∥
λ
k
∥
∞
\mu_k>\Vert\lambda_k\Vert_{\infty}
μ k > ∥ λ k ∥ ∞
λ
k
\lambda_k
λ k
x
k
x_k
x k
μ
k
\mu_k
μ k
因选取合适
μ
k
\mu_k
μ k
在选取初始点
x
k
+
1
s
x_{k+1}^s
x k + 1 s
μ
k
\mu_k
μ k
x
k
+
1
s
x_{k+1}^s
x k + 1 s
ϕ
1
(
x
;
μ
k
)
\phi_1(x;\mu_k)
ϕ 1 ( x ; μ k )
x
k
x_k
x k
精确非光滑罚函数可以定义为除了
l
1
l_1
l 1
ϕ
(
x
;
μ
)
=
f
(
x
)
+
μ
∥
c
E
(
x
)
∥
+
μ
∥
[
c
I
(
x
)
]
−
∥
,
\phi(x;\mu)=f(x)+\mu\Vert c_{\mathcal{E}}(x)\Vert+\mu\Vert[c_{\mathcal{I}}(x)]^-\Vert,
ϕ ( x ; μ ) = f ( x ) + μ ∥ c E ( x ) ∥ + μ ∥ [ c I ( x ) ] − ∥ ,
∥
⋅
∥
\Vert\cdot\Vert
∥ ⋅ ∥
c
E
,
c
I
c_{\mathcal{E}},c_{\mathcal{I}}
c E , c I
h
(
x
)
=
∥
c
E
(
x
)
∥
+
∥
[
c
I
(
x
)
]
−
∥
h(x)=\Vert c_{\mathcal{E}}(x)\Vert+\Vert[c_{\mathcal{I}}(x)]^-\Vert
h ( x ) = ∥ c E ( x ) ∥ + ∥ [ c I ( x ) ] − ∥ 一一对应 的, 证明可见Han S P和Mangasarian O L的定理4.2. 最常用的范数为
l
1
,
l
∞
,
l
2
l_1,l_{\infty},l_2
l 1 , l ∞ , l 2
l
∞
l_{\infty}
l ∞
对
l
1
l_1
l 1
μ
≥
μ
∗
=
∥
λ
∗
∥
D
,
\mu\ge\mu^*=\Vert\lambda^*\Vert_D,
μ ≥ μ ∗ = ∥ λ ∗ ∥ D ,
∥
⋅
∥
D
\Vert\cdot\Vert_D
∥ ⋅ ∥ D
∥
⋅
∥
\Vert\cdot\Vert
∥ ⋅ ∥ 对偶范数 . 而定理4则无需修改直接可应用.
下说明此类 的罚函数若是精确的必是非光滑的. 为说明简单, 我们仅考虑只有一个等式约束
c
1
(
x
)
=
0
c_1(x)=0
c 1 ( x ) = 0
ϕ
(
x
;
μ
)
=
f
(
x
)
+
μ
h
(
c
i
(
x
)
)
,
\phi(x;\mu)=f(x)+\mu h(c_i(x)),
ϕ ( x ; μ ) = f ( x ) + μ h ( c i ( x ) ) ,
h
:
R
→
R
h:\mathbb{R}\to\mathbb{R}
h : R → R
h
(
y
)
≥
0
,
∀
y
∈
R
;
h
(
0
)
=
0
h(y)\ge0,\forall y\in\mathbb{R};h(0)=0
h ( y ) ≥ 0 , ∀ y ∈ R ; h ( 0 ) = 0
h
h
h
h
h
h
0
0
0
∇
h
(
0
)
=
0
\nabla h(0)=0
∇ h ( 0 ) = 0
x
∗
x^*
x ∗
c
i
(
x
∗
)
=
0
⇒
∇
h
(
c
1
(
x
∗
)
)
=
0
c_i(x^*)=0\Rightarrow\nabla h(c_1(x^*))=0
c i ( x ∗ ) = 0 ⇒ ∇ h ( c 1 ( x ∗ ) ) = 0
x
∗
x^*
x ∗
ϕ
(
x
;
μ
)
\phi(x;\mu)
ϕ ( x ; μ )
μ
\mu
μ
0
=
∇
ϕ
(
x
∗
;
μ
)
=
∇
f
(
x
∗
)
+
μ
∇
c
i
(
x
∗
)
∇
h
(
c
1
(
x
∗
)
)
=
∇
f
(
x
∗
)
.
0=\nabla\phi(x^*;\mu)=\nabla f(x^*)+\mu\nabla c_i(x^*)\nabla h(c_1(x^*))=\nabla f(x^*).
0 = ∇ ϕ ( x ∗ ; μ ) = ∇ f ( x ∗ ) + μ ∇ c i ( x ∗ ) ∇ h ( c 1 ( x ∗ ) ) = ∇ f ( x ∗ ) .
f
f
f
h
h
h
ϕ
(
⋅
;
μ
)
\phi(\cdot;\mu)
ϕ ( ⋅ ; μ )
非光滑罚函数也可用作其他机制下计算迭代步时的价值函数 . 具体可见第十五章第四节的一般性讨论和第十八和第十九章中的具体实施.
下面我们讨论一种被称为乘子法the method of multipliers 或增广Lagrange函数法augmented Lagragian methods 的方法. 此法与第1节中的二次罚函数法相关, 但它通过显式引入Lagrange乘子估计 至目标函数, 减小了问题的病态程度 . 引入显式Lagrange乘子估计后的函数就被称为增广Lagrange函数(augmented Lagrangian function) . 与第2节中讨论的罚函数相反, 增广Lagrange函数极大地保留了光滑性 , 因此具体实施可调用标准的无约束或带界约束的优化软件求解.
我们首先考虑等式约束问题. 二次罚函数
Q
(
x
;
μ
)
Q(x;\mu)
Q ( x ; μ )
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k )
x
k
x_k
x k 并不满足可行性条件
c
i
(
x
)
=
0
,
i
∈
E
c_i(x)=0,i\in\mathcal{E}
c i ( x ) = 0 , i ∈ E
c
i
(
x
k
)
≈
−
λ
i
∗
/
μ
k
,
∀
i
∈
E
.
c_i(x_k)\approx-\lambda_i^*/\mu_k,\quad\forall i\in\mathcal{E}.
c i ( x k ) ≈ − λ i ∗ / μ k , ∀ i ∈ E .
c
i
(
x
k
)
→
0
,
μ
k
→
∞
c_i(x_k)\to0,\mu_k\to\infty
c i ( x k ) → 0 , μ k → ∞ 修改函数
Q
(
x
;
μ
k
)
Q(x;\mu_k)
Q ( x ; μ k ) 来避免这种系统上的偏差, 即使得近似极小点无需
μ
k
\mu_k
μ k
c
i
(
x
)
=
0
c_i(x)=0
c i ( x ) = 0
增广Lagrange函数
L
A
(
x
,
λ
;
μ
)
\mathcal{L}_A(x,\lambda;\mu)
L A ( x , λ ; μ )
λ
\lambda
λ
L
A
(
x
,
λ
;
μ
)
=
d
e
f
f
(
x
)
−
∑
i
∈
E
λ
i
c
i
(
x
)
+
μ
2
∑
i
∈
E
c
i
2
(
x
)
.
\mathcal{L}_A(x,\lambda;\mu)\xlongequal{def}f(x)-\sum_{i\in\mathcal{E}}\lambda_ic_i(x)+\frac{\mu}{2}\sum_{i\in\mathcal{E}}c_i^2(x).
L A ( x , λ ; μ ) d e f
f ( x ) − i ∈ E ∑ λ i c i ( x ) + 2 μ i ∈ E ∑ c i 2 ( x ) .
λ
\lambda
λ Lagrange函数和二次罚函数的结合 .
下面我们设计一种对
x
x
x
μ
\mu
μ
μ
k
>
0
\mu_k>0
μ k > 0
λ
\lambda
λ
λ
k
\lambda^k
λ k
x
k
x_k
x k
L
A
(
x
,
λ
k
;
μ
k
)
\mathcal{L}_A(x,\lambda^k;\mu_k)
L A ( x , λ k ; μ k )
0
=
∇
x
L
A
(
x
k
,
λ
k
;
μ
k
)
=
∇
f
(
x
k
)
−
∑
i
∈
E
[
λ
i
k
−
μ
k
c
i
(
x
k
)
]
∇
c
i
(
x
k
)
.
0=\nabla_x\mathcal{L}_A(x_k,\lambda^k;\mu_k)=\nabla f(x_k)-\sum_{i\in\mathcal{E}}[\lambda_i^k-\mu_kc_i(x_k)]\nabla c_i(x_k).
0 = ∇ x L A ( x k , λ k ; μ k ) = ∇ f ( x k ) − i ∈ E ∑ [ λ i k − μ k c i ( x k ) ] ∇ c i ( x k ) .
∇
c
i
(
x
k
)
\nabla c_i(x_k)
∇ c i ( x k )
λ
i
∗
≈
λ
i
k
−
μ
k
c
i
(
x
k
)
,
∀
i
∈
E
.
\lambda_i^*\approx\lambda_i^k-\mu_kc_i(x_k),\quad\forall i\in\mathcal{E}.
λ i ∗ ≈ λ i k − μ k c i ( x k ) , ∀ i ∈ E .
c
i
(
x
k
)
≈
−
1
μ
k
(
λ
i
∗
−
λ
i
k
)
,
∀
i
∈
E
,
c_i(x_k)\approx-\frac{1}{\mu_k}(\lambda_i^*-\lambda_i^k),\quad\forall i\in\mathcal{E},
c i ( x k ) ≈ − μ k 1 ( λ i ∗ − λ i k ) , ∀ i ∈ E ,
λ
k
\lambda^k
λ k
λ
∗
\lambda^*
λ ∗
x
k
x_k
x k
(
1
/
μ
k
)
(1/\mu_k)
( 1 / μ k )
λ
k
\lambda^k
λ k
λ
i
k
+
1
=
λ
i
k
−
μ
k
c
i
(
x
k
)
,
∀
i
∈
E
.
\lambda_i^{k+1}=\lambda_i^k-\mu_kc_i(x_k),\quad\forall i\in\mathcal{E}.
λ i k + 1 = λ i k − μ k c i ( x k ) , ∀ i ∈ E .
于是我们得到下述算法框架.
框架3 (Augmented Lagrangian Method-Equality Constraints)
μ
0
>
0
\mu_0>0
μ 0 > 0
τ
0
>
0
\tau_0>0
τ 0 > 0
x
0
s
x_0^s
x 0 s
λ
0
\lambda^0
λ 0
k
=
0
,
1
,
2
,
…
k=0,1,2,\ldots
k = 0 , 1 , 2 , …
\quad\quad
x
k
x_k
x k
L
A
(
⋅
,
λ
k
;
μ
k
)
\mathcal{L}_A(\cdot,\lambda^k;\mu_k)
L A ( ⋅ , λ k ; μ k )
x
k
s
x_k^s
x k s
∥
∇
x
L
A
(
x
k
,
λ
k
;
μ
k
)
∥
≤
τ
k
\Vert\nabla_x\mathcal{L}_A(x_k,\lambda^k;\mu_k)\Vert\le\tau_k
∥ ∇ x L A ( x k , λ k ; μ k ) ∥ ≤ τ k
\quad\quad
\quad\quad\quad\quad
x
k
x_k
x k
\quad\quad
\quad\quad
λ
k
+
1
\lambda^{k+1}
λ k + 1
\quad\quad
μ
k
+
1
≥
μ
k
\mu_{k+1}\ge\mu_k
μ k + 1 ≥ μ k
\quad\quad
x
k
+
1
s
=
x
k
x_{k+1}^s=x_k
x k + 1 s = x k
\quad\quad
τ
k
+
1
\tau_{k+1}
τ k + 1
我们通过一个例子来阐释此法可以无需将
μ
\mu
μ
∞
\infty
∞
x
k
+
1
s
x_{k+1}^s
x k + 1 s
τ
k
\tau_k
τ k
∑
i
∈
E
∣
c
(
x
k
)
∣
\sum_{i\in\mathcal{E}}|c(x_k)|
∑ i ∈ E ∣ c ( x k ) ∣
μ
\mu
μ
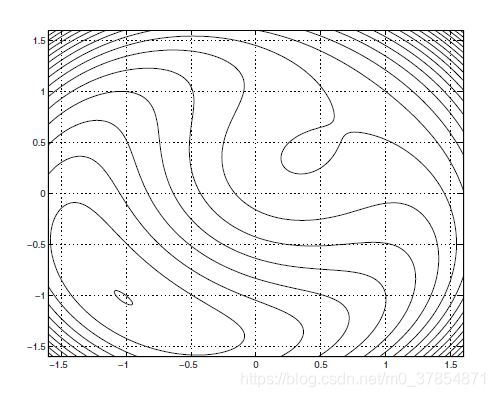
例4 再次考虑例1中的问题, 其增广Lagrange函数为
L
A
(
x
,
λ
;
μ
)
=
x
1
+
x
2
−
λ
(
x
1
2
+
x
2
2
−
2
)
+
μ
2
(
x
1
2
+
x
2
2
−
2
)
2
.
\mathcal{L}_A(x,\lambda;\mu)=x_1+x_2-\lambda(x_1^2+x_2^2-2)+\frac{\mu}{2}(x_1^2+x_2^2-2)^2.
L A ( x , λ ; μ ) = x 1 + x 2 − λ ( x 1 2 + x 2 2 − 2 ) + 2 μ ( x 1 2 + x 2 2 − 2 ) 2 .
x
∗
=
(
−
1
,
−
1
)
T
x^*=(-1,-1)^T
x ∗ = ( − 1 , − 1 ) T
λ
∗
=
−
0.5
\lambda^*=-0.5
λ ∗ = − 0 . 5
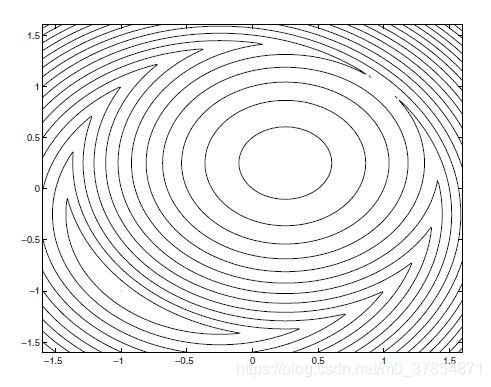
k
k
k
μ
k
=
1
\mu_k=1
μ k = 1
λ
k
=
−
0.4
\lambda^k=-0.4
λ k = − 0 . 4
μ
k
=
1
\mu_k=1
μ k = 1
注意到等高线之间的跨度说明此问题的条件数与二次罚函数
Q
(
x
;
1
)
Q(x;1)
Q ( x ; 1 )
x
k
≈
(
−
1.02
,
−
1.02
)
T
x_k\approx(-1.02,-1.02)^T
x k ≈ ( − 1 . 0 2 , − 1 . 0 2 ) T
x
∗
=
(
−
1
,
−
1
)
T
x^*=(-1,-1)^T
x ∗ = ( − 1 , − 1 ) T
L
A
(
x
,
λ
;
μ
)
\mathcal{L}_A(x,\lambda;\mu)
L A ( x , λ ; μ )
下面我们证明关于增广Lagrange函数使用和等式约束问题乘子法的两条结论.
第一条证实, 若我们有精确Lagrange乘子
λ
∗
\lambda^*
λ ∗
x
∗
x^*
x ∗
L
A
(
x
,
λ
∗
;
μ
)
,
μ
\mathcal{L}_A(x,\lambda^*;\mu),\mu
L A ( x , λ ∗ ; μ ) , μ
λ
∗
\lambda^*
λ ∗ 只要
λ
\lambda
λ
λ
∗
\lambda^*
λ ∗
μ
\mu
μ
L
A
(
x
,
λ
;
μ
)
\mathcal{L}_A(x,\lambda;\mu)
L A ( x , λ ; μ )
x
∗
x^*
x ∗ .
定理5 令
x
∗
x^*
x ∗
λ
=
λ
∗
\lambda=\lambda^*
λ = λ ∗
μ
ˉ
\bar{\mu}
μ ˉ
∀
μ
≥
μ
ˉ
\forall\mu\ge\bar{\mu}
∀ μ ≥ μ ˉ
x
∗
x^*
x ∗
L
A
(
x
,
λ
∗
;
μ
)
\mathcal{L}_A(x,\lambda^*;\mu)
L A ( x , λ ∗ ; μ )
证明: 我们证明
x
∗
x^*
x ∗
μ
\mu
μ
L
A
(
x
,
λ
∗
;
μ
)
\mathcal{L}_A(x,\lambda^*;\mu)
L A ( x , λ ∗ ; μ )
∇
x
L
A
(
x
∗
,
λ
∗
;
μ
)
=
0
,
∇
x
x
2
L
A
(
x
∗
,
λ
∗
;
μ
)
正
定
.
\nabla_x\mathcal{L}_A(x^*,\lambda^*;\mu)=0,\quad\nabla^2_{xx}\mathcal{L}_A(x^*,\lambda^*;\mu)正定.
∇ x L A ( x ∗ , λ ∗ ; μ ) = 0 , ∇ x x 2 L A ( x ∗ , λ ∗ ; μ ) 正 定 .
x
∗
x^*
x ∗
∇
x
L
(
x
∗
,
λ
∗
)
=
0
,
c
i
(
x
∗
)
=
0
,
∀
i
∈
E
\nabla_x\mathcal{L}(x^*,\lambda^*)=0,c_i(x^*)=0,\forall i\in\mathcal{E}
∇ x L ( x ∗ , λ ∗ ) = 0 , c i ( x ∗ ) = 0 , ∀ i ∈ E
∇
x
L
A
(
x
∗
,
λ
∗
;
μ
)
=
∇
f
(
x
∗
)
−
∑
i
∈
E
[
λ
i
∗
−
μ
c
i
(
x
∗
)
]
∇
c
i
(
x
∗
)
=
∇
f
(
x
∗
)
−
∑
i
∈
E
λ
i
∗
∇
c
i
(
x
∗
)
=
∇
x
L
(
x
∗
,
λ
∗
)
=
0
,
\begin{aligned}\nabla_x\mathcal{L}_A(x^*,\lambda^*;\mu)&=\nabla f(x^*)-\sum_{i\in\mathcal{E}}[\lambda_i^*-\mu c_i(x^*)]\nabla c_i(x^*)\\&=\nabla f(x^*)-\sum_{i\in\mathcal{E}}\lambda_i^*\nabla c_i(x^*)=\nabla_x\mathcal{L}(x^*,\lambda^*)=0,\end{aligned}
∇ x L A ( x ∗ , λ ∗ ; μ ) = ∇ f ( x ∗ ) − i ∈ E ∑ [ λ i ∗ − μ c i ( x ∗ ) ] ∇ c i ( x ∗ ) = ∇ f ( x ∗ ) − i ∈ E ∑ λ i ∗ ∇ c i ( x ∗ ) = ∇ x L ( x ∗ , λ ∗ ) = 0 ,
μ
\mu
μ
A
A
A
∇
x
x
2
L
A
(
x
∗
,
λ
∗
;
μ
)
=
∇
x
x
2
L
(
x
∗
,
λ
∗
)
+
μ
A
T
A
.
\nabla^2_{xx}\mathcal{L}_A(x^*,\lambda^*;\mu)=\nabla^2_{xx}\mathcal{L}(x^*,\lambda^*)+\mu A^TA.
∇ x x 2 L A ( x ∗ , λ ∗ ; μ ) = ∇ x x 2 L ( x ∗ , λ ∗ ) + μ A T A .
μ
\mu
μ
k
≥
1
k\ge1
k ≥ 1
w
k
:
∥
w
k
∥
=
1
w_k:\Vert w_k\Vert=1
w k : ∥ w k ∥ = 1
0
≥
w
k
T
∇
x
x
2
L
A
(
x
∗
,
λ
∗
;
k
)
w
k
=
w
k
T
∇
x
x
2
L
(
x
∗
,
λ
∗
)
w
k
+
k
∥
A
w
k
∥
2
2
,
0\ge w_k^T\nabla^2_{xx}\mathcal{L}_A(x^*,\lambda^*;k)w_k=w_k^T\nabla^2_{xx}\mathcal{L}(x^*,\lambda^*)w_k+k\Vert Aw_k\Vert^2_2,
0 ≥ w k T ∇ x x 2 L A ( x ∗ , λ ∗ ; k ) w k = w k T ∇ x x 2 L ( x ∗ , λ ∗ ) w k + k ∥ A w k ∥ 2 2 ,
∥
A
w
k
∥
2
2
≤
−
(
1
/
k
)
w
k
T
∇
x
x
2
L
(
x
∗
,
λ
∗
)
w
k
→
0
,
k
→
∞
.
\Vert Aw_k\Vert_2^2\le-(1/k)w_k^T\nabla^2_{xx}\mathcal{L}(x^*,\lambda^*)w_k\to0,\quad k\to\infty.
∥ A w k ∥ 2 2 ≤ − ( 1 / k ) w k T ∇ x x 2 L ( x ∗ , λ ∗ ) w k → 0 , k → ∞ .
{
w
k
}
\{w_k\}
{ w k }
w
w
w
A
w
=
0
Aw=0
A w = 0
w
∈
F
(
x
∗
)
w\in\mathcal{F}(x^*)
w ∈ F ( x ∗ )
w
k
T
∇
x
x
2
L
(
x
∗
,
λ
∗
)
w
k
≤
−
k
∥
A
w
k
∥
2
2
≤
0
,
w_k^T\nabla^2_{xx}\mathcal{L}(x^*,\lambda^*)w_k\le-k\Vert Aw_k\Vert_2^2\le0,
w k T ∇ x x 2 L ( x ∗ , λ ∗ ) w k ≤ − k ∥ A w k ∥ 2 2 ≤ 0 ,
w
T
∇
x
x
2
L
(
x
∗
,
λ
∗
)
w
≤
0
w^T\nabla^2_{xx}\mathcal{L}(x^*,\lambda^*)w\le0
w T ∇ x x 2 L ( x ∗ , λ ∗ ) w ≤ 0
第二条结论则立意于更实际的情形
λ
≠
λ
∗
\lambda\ne\lambda^*
λ ̸ = λ ∗
L
A
(
x
,
λ
;
μ
)
\mathcal{L}_A(x,\lambda;\mu)
L A ( x , λ ; μ )
x
∗
x^*
x ∗
x
k
x_k
x k
λ
k
+
1
\lambda^{k+1}
λ k + 1
x
∗
,
λ
∗
x^*,\lambda^*
x ∗ , λ ∗
定理6 设定理5的条件在
x
∗
,
λ
∗
x^*,\lambda^*
x ∗ , λ ∗
μ
ˉ
\bar{\mu}
μ ˉ
δ
,
ϵ
,
M
\delta,\epsilon,M
δ , ϵ , M
对所有满足
∥
λ
k
−
λ
∗
∥
≤
μ
k
δ
,
μ
k
≥
μ
ˉ
\Vert\lambda^k-\lambda^*\Vert\le\mu_k\delta,\quad\mu_k\ge\bar{\mu}
∥ λ k − λ ∗ ∥ ≤ μ k δ , μ k ≥ μ ˉ
λ
k
,
μ
k
\lambda^k,\mu_k
λ k , μ k
min
x
L
A
(
x
,
λ
k
;
μ
k
)
,
s
u
b
j
e
c
t
 
t
o
 
∥
x
−
x
∗
∥
≤
ϵ
\min_x\mathcal{L}_A(x,\lambda^k;\mu_k),\quad\mathrm{subject\,to\,}\Vert x-x^*\Vert\le\epsilon
x min L A ( x , λ k ; μ k ) , s u b j e c t t o ∥ x − x ∗ ∥ ≤ ϵ
x
k
x_k
x k
∥
x
k
−
x
∗
∥
≤
M
∥
λ
k
−
λ
∗
∥
/
μ
k
.
\Vert x_k-x^*\Vert\le M\Vert\lambda^k-\lambda^*\Vert/\mu_k.
∥ x k − x ∗ ∥ ≤ M ∥ λ k − λ ∗ ∥ / μ k .
对所有满足
∥
λ
k
−
λ
∗
∥
≤
μ
k
δ
,
μ
k
≥
μ
ˉ
\Vert\lambda^k-\lambda^*\Vert\le\mu_k\delta,\quad\mu_k\ge\bar{\mu}
∥ λ k − λ ∗ ∥ ≤ μ k δ , μ k ≥ μ ˉ
λ
k
,
μ
k
\lambda^k,\mu_k
λ k , μ k
∥
λ
k
+
1
−
λ
∗
∥
≤
M
∥
λ
k
−
λ
∗
∥
/
μ
k
,
\Vert\lambda^{k+1}-\lambda^*\Vert\le M\Vert\lambda^k-\lambda^*\Vert/\mu_k,
∥ λ k + 1 − λ ∗ ∥ ≤ M ∥ λ k − λ ∗ ∥ / μ k ,
λ
k
+
1
\lambda^{k+1}
λ k + 1
λ
i
k
+
1
=
λ
i
k
−
μ
k
c
i
(
x
k
)
,
∀
i
∈
E
\lambda_i^{k+1}=\lambda_i^k-\mu_kc_i(x_k),\quad\forall i\in\mathcal{E}
λ i k + 1 = λ i k − μ k c i ( x k ) , ∀ i ∈ E
对所有满足
∥
λ
k
−
λ
∗
∥
≤
μ
k
δ
,
μ
k
≥
μ
ˉ
\Vert\lambda^k-\lambda^*\Vert\le\mu_k\delta,\quad\mu_k\ge\bar{\mu}
∥ λ k − λ ∗ ∥ ≤ μ k δ , μ k ≥ μ ˉ
λ
k
,
μ
k
\lambda^k,\mu_k
λ k , μ k
∇
x
x
2
L
A
(
x
k
,
λ
k
;
μ
k
)
\nabla^2_{xx}\mathcal{L}_A(x_k,\lambda^k;\mu_k)
∇ x x 2 L A ( x k , λ k ; μ k )
∇
c
i
(
x
k
)
,
i
∈
E
\nabla c_i(x_k),i\in\mathcal{E}
∇ c i ( x k ) , i ∈ E
证明: 以下以
μ
,
λ
,
λ
~
\mu,\lambda,\tilde\lambda
μ , λ , λ ~
μ
k
,
λ
k
,
λ
k
+
1
\mu_k,\lambda^k,\lambda^{k+1}
μ k , λ k , λ k + 1
μ
>
0
\mu>0
μ > 0
(
x
,
λ
~
,
λ
,
μ
)
(x,\tilde\lambda,\lambda,\mu)
( x , λ ~ , λ , μ )
∇
f
(
x
)
−
∇
h
(
x
)
λ
~
=
0
,
h
(
x
)
+
(
λ
−
λ
~
)
/
μ
=
0
,
\nabla f(x)-\nabla h(x)\tilde\lambda=0,\quad h(x)+(\lambda-\tilde\lambda)/\mu=0,
∇ f ( x ) − ∇ h ( x ) λ ~ = 0 , h ( x ) + ( λ − λ ~ ) / μ = 0 ,
h
(
x
)
=
[
c
1
(
x
)
c
2
(
x
)
⋮
c
m
(
x
)
]
,
∇
h
(
x
)
=
[
∇
c
1
(
x
)
∇
c
2
(
x
)
⋯
∇
c
m
(
x
)
]
.
h(x)=\begin{bmatrix}c_1(x)\\c_2(x)\\\vdots\\c_m(x)\end{bmatrix},\quad \nabla h(x)=\begin{bmatrix}\nabla c_1(x) & \nabla c_2(x) & \cdots & \nabla c_m(x)\end{bmatrix}.
h ( x ) = ⎣ ⎢ ⎢ ⎢ ⎡ c 1 ( x ) c 2 ( x ) ⋮ c m ( x ) ⎦ ⎥ ⎥ ⎥ ⎤ , ∇ h ( x ) = [ ∇ c 1 ( x ) ∇ c 2 ( x ) ⋯ ∇ c m ( x ) ] .
t
∈
R
m
,
γ
∈
R
t\in\mathbb{R}^m,\gamma\in\mathbb{R}
t ∈ R m , γ ∈ R
t
=
(
λ
−
λ
∗
)
/
μ
,
γ
=
1
/
μ
,
t=(\lambda-\lambda^*)/\mu,\quad\gamma=1/\mu,
t = ( λ − λ ∗ ) / μ , γ = 1 / μ ,
∇
f
(
x
)
−
∇
h
(
x
)
λ
~
=
0
,
h
(
x
)
+
t
+
γ
λ
∗
−
γ
λ
~
=
0.
\nabla f(x)-\nabla h(x)\tilde\lambda=0,\quad h(x)+t+\gamma\lambda^*-\gamma\tilde\lambda=0.
∇ f ( x ) − ∇ h ( x ) λ ~ = 0 , h ( x ) + t + γ λ ∗ − γ λ ~ = 0 .
t
=
0
,
γ
∈
[
0
,
1
/
μ
ˉ
]
t=0,\gamma\in[0,1/\bar{\mu}]
t = 0 , γ ∈ [ 0 , 1 / μ ˉ ]
x
=
x
∗
,
λ
~
=
λ
∗
x=x^*,\tilde\lambda=\lambda^*
x = x ∗ , λ ~ = λ ∗
(
x
,
λ
~
)
(x,\tilde\lambda)
( x , λ ~ )
[
∇
x
x
2
L
(
x
∗
,
λ
∗
)
∇
h
(
x
∗
)
−
∇
h
(
x
∗
)
T
−
γ
I
]
.
\begin{bmatrix}\nabla^2_{xx}\mathcal{L}(x^*,\lambda^*) & \nabla h(x^*)\\-\nabla h(x^*)^T & -\gamma I\end{bmatrix}.
[ ∇ x x 2 L ( x ∗ , λ ∗ ) − ∇ h ( x ∗ ) T ∇ h ( x ∗ ) − γ I ] .
γ
∈
[
0
,
1
/
μ
ˉ
]
\gamma\in[0,1/\bar\mu]
γ ∈ [ 0 , 1 / μ ˉ ]
γ
=
0
\gamma=0
γ = 0
∀
γ
∈
(
0
,
1
/
μ
ˉ
]
\forall\gamma\in(0,1/\bar\mu]
∀ γ ∈ ( 0 , 1 / μ ˉ ]
z
∈
R
n
,
w
∈
R
m
z\in\mathbb{R}^n,w\in\mathbb{R}^m
z ∈ R n , w ∈ R m
[
∇
x
x
2
L
(
x
∗
,
λ
∗
)
∇
h
(
x
∗
)
−
∇
h
(
x
∗
)
T
−
γ
I
]
[
z
w
]
=
0
\begin{bmatrix}\nabla^2_{xx}\mathcal{L}(x^*,\lambda^*) & \nabla h(x^*)\\-\nabla h(x^*)^T & -\gamma I\end{bmatrix}\begin{bmatrix}z\\w\end{bmatrix}=0
[ ∇ x x 2 L ( x ∗ , λ ∗ ) − ∇ h ( x ∗ ) T ∇ h ( x ∗ ) − γ I ] [ z w ] = 0
∇
x
x
2
L
(
x
∗
,
λ
∗
)
z
+
∇
h
(
x
∗
)
w
=
0
,
−
∇
h
(
x
∗
)
T
z
−
γ
w
=
0.
\begin{aligned}\nabla^2_{xx}\mathcal{L}(x^*,\lambda^*)z+\nabla h(x^*)w&=0,\\-\nabla h(x^*)^Tz-\gamma w&=0.\end{aligned}
∇ x x 2 L ( x ∗ , λ ∗ ) z + ∇ h ( x ∗ ) w − ∇ h ( x ∗ ) T z − γ w = 0 , = 0 .
w
w
w
[
∇
x
x
2
L
(
x
∗
,
λ
∗
)
−
(
1
/
γ
)
∇
h
(
x
∗
)
∇
h
(
x
∗
)
T
]
z
=
0.
[\nabla^2_{xx}\mathcal{L}(x^*,\lambda^*)-(1/\gamma)\nabla h(x^*)\nabla h(x^*)^T]z=0.
[ ∇ x x 2 L ( x ∗ , λ ∗ ) − ( 1 / γ ) ∇ h ( x ∗ ) ∇ h ( x ∗ ) T ] z = 0 .
γ
=
1
/
μ
,
μ
≥
μ
ˉ
\gamma=1/\mu,\mu\ge\bar\mu
γ = 1 / μ , μ ≥ μ ˉ
∇
x
x
2
L
A
(
x
∗
,
λ
∗
;
μ
)
z
=
0
\nabla^2_{xx}\mathcal{L}_A(x^*,\lambda^*;\mu)z=0
∇ x x 2 L A ( x ∗ , λ ∗ ; μ ) z = 0
∇
x
x
2
L
A
(
x
∗
,
λ
∗
;
μ
)
>
0
,
μ
≥
μ
ˉ
\nabla^2_{xx}\mathcal{L}_A(x^*,\lambda^*;\mu)>0,\mu\ge\bar\mu
∇ x x 2 L A ( x ∗ , λ ∗ ; μ ) > 0 , μ ≥ μ ˉ
z
=
0
⇒
w
=
0
z=0\Rightarrow w=0
z = 0 ⇒ w = 0
γ
∈
[
0
,
1
/
μ
ˉ
]
\gamma\in[0,1/\bar\mu]
γ ∈ [ 0 , 1 / μ ˉ ]
ϵ
>
0
,
δ
>
0
\epsilon>0,\delta>0
ϵ > 0 , δ > 0
S
(
K
;
δ
)
S(K;\delta)
S ( K ; δ )
K
=
{
(
0
,
γ
)
∣
γ
∈
[
0
,
1
/
μ
ˉ
]
}
K=\{(0,\gamma)\mid\gamma\in[0,1/\bar\mu]\}
K = { ( 0 , γ ) ∣ γ ∈ [ 0 , 1 / μ ˉ ] }
x
^
(
t
,
γ
)
,
λ
^
(
t
,
γ
)
\hat x(t,\gamma),\hat\lambda(t,\gamma)
x ^ ( t , γ ) , λ ^ ( t , γ )
(
∣
x
^
(
t
,
γ
)
−
x
∗
∣
2
+
∣
λ
^
(
t
,
γ
)
−
λ
∗
∣
2
)
1
/
2
<
ϵ
,
∀
(
t
,
γ
)
∈
S
(
K
;
δ
)
,
\left(|\hat{x}(t,\gamma)-x^*|^2+|\hat{\lambda}(t,\gamma)-\lambda^*|^2\right)^{1/2}<\epsilon,\forall(t,\gamma)\in S(K;\delta),
( ∣ x ^ ( t , γ ) − x ∗ ∣ 2 + ∣ λ ^ ( t , γ ) − λ ∗ ∣ 2 ) 1 / 2 < ϵ , ∀ ( t , γ ) ∈ S ( K ; δ ) ,
∇
f
[
x
^
(
t
,
γ
)
]
−
∇
h
[
x
^
(
t
,
γ
)
]
λ
^
(
t
,
γ
)
=
0
,
h
[
x
^
(
t
,
γ
)
]
+
t
+
γ
λ
∗
−
γ
λ
^
(
t
,
γ
)
=
0.
\begin{aligned}\nabla f[\hat{x}(t,\gamma)]-\nabla h[\hat{x}(t,\gamma)]\hat{\lambda}(t,\gamma)&=0,\\h[\hat{x}(t,\gamma)]+t+\gamma\lambda^*-\gamma\hat\lambda(t,\gamma)&=0.\end{aligned}
∇ f [ x ^ ( t , γ ) ] − ∇ h [ x ^ ( t , γ ) ] λ ^ ( t , γ ) h [ x ^ ( t , γ ) ] + t + γ λ ∗ − γ λ ^ ( t , γ ) = 0 , = 0 .
δ
,
ϵ
\delta,\epsilon
δ , ϵ
∇
h
[
x
^
(
t
,
γ
)
]
\nabla h[\hat{x}(t,\gamma)]
∇ h [ x ^ ( t , γ ) ]
m
m
m
∇
x
x
2
L
[
x
^
(
t
,
γ
)
,
λ
^
(
t
,
γ
)
]
−
μ
∇
h
[
x
^
(
t
,
γ
)
]
∇
h
[
x
^
(
t
,
γ
)
]
T
>
0
,
∀
(
t
,
γ
)
∈
S
(
K
;
δ
)
,
μ
≥
μ
ˉ
.
\nabla^2_{xx}\mathcal{L}[\hat{x}(t,\gamma),\hat{\lambda}(t,\gamma)]-\mu\nabla h[\hat x(t,\gamma)]\nabla h[\hat x(t,\gamma)]^T>0,\forall (t,\gamma)\in S(K;\delta),\mu\ge\bar\mu.
∇ x x 2 L [ x ^ ( t , γ ) , λ ^ ( t , γ ) ] − μ ∇ h [ x ^ ( t , γ ) ] ∇ h [ x ^ ( t , γ ) ] T > 0 , ∀ ( t , γ ) ∈ S ( K ; δ ) , μ ≥ μ ˉ .
μ
≥
μ
ˉ
,
∥
λ
−
λ
∗
∥
≤
δ
μ
\mu\ge\bar\mu,\Vert\lambda-\lambda^*\Vert\le\delta\mu
μ ≥ μ ˉ , ∥ λ − λ ∗ ∥ ≤ δ μ
x
(
λ
,
μ
)
=
x
^
(
λ
−
λ
∗
μ
,
1
μ
)
,
λ
~
(
λ
,
μ
)
=
λ
^
(
λ
−
λ
∗
μ
,
1
μ
)
.
x(\lambda,\mu)=\hat{x}\left(\frac{\lambda-\lambda^*}{\mu},\frac{1}{\mu}\right),\quad\tilde\lambda(\lambda,\mu)=\hat\lambda\left(\frac{\lambda-\lambda^*}{\mu},\frac{1}{\mu}\right).
x ( λ , μ ) = x ^ ( μ λ − λ ∗ , μ 1 ) , λ ~ ( λ , μ ) = λ ^ ( μ λ − λ ∗ , μ 1 ) .
∥
λ
−
λ
∗
∥
≤
μ
δ
,
μ
≥
μ
ˉ
\Vert\lambda-\lambda^*\Vert\le\mu\delta,\quad\mu\ge\bar{\mu}
∥ λ − λ ∗ ∥ ≤ μ δ , μ ≥ μ ˉ
λ
k
,
μ
k
\lambda^k,\mu_k
λ k , μ k
∇
f
[
x
(
λ
,
μ
)
]
−
∇
h
[
x
(
λ
,
c
)
]
λ
~
(
λ
,
μ
)
=
0
,
λ
~
(
λ
,
μ
)
=
λ
−
μ
h
[
x
(
λ
,
μ
)
]
,
∇
x
x
2
L
[
x
(
λ
,
μ
)
,
λ
~
(
λ
,
μ
)
]
−
μ
∇
h
[
x
(
λ
,
μ
)
]
∇
h
[
x
(
λ
,
μ
)
]
T
=
∇
x
x
2
L
A
[
x
(
λ
,
μ
)
,
λ
]
>
0.
\begin{aligned}\nabla f[x(\lambda,\mu)]-\nabla h[x(\lambda,c)]\tilde\lambda(\lambda,\mu)&=0,\\\tilde\lambda(\lambda,\mu)&=\lambda-\mu h[x(\lambda,\mu)],\\\nabla^2_{xx}\mathcal{L}[x(\lambda,\mu),\tilde\lambda(\lambda,\mu)]-\mu\nabla h[x(\lambda,\mu)]\nabla h[x(\lambda,\mu)]^T=\nabla^2_{xx}\mathcal{L}_A[x(\lambda,\mu),\lambda]&>0.\end{aligned}
∇ f [ x ( λ , μ ) ] − ∇ h [ x ( λ , c ) ] λ ~ ( λ , μ ) λ ~ ( λ , μ ) ∇ x x 2 L [ x ( λ , μ ) , λ ~ ( λ , μ ) ] − μ ∇ h [ x ( λ , μ ) ] ∇ h [ x ( λ , μ ) ] T = ∇ x x 2 L A [ x ( λ , μ ) , λ ] = 0 , = λ − μ h [ x ( λ , μ ) ] , > 0 .
∇
f
[
x
^
(
t
,
γ
)
]
−
∇
h
[
x
^
(
t
,
γ
)
]
λ
^
(
t
,
γ
)
=
0
,
h
[
x
^
(
t
,
γ
)
]
+
t
+
γ
λ
∗
−
γ
λ
^
(
t
,
γ
)
=
0.
\begin{aligned}\nabla f[\hat{x}(t,\gamma)]-\nabla h[\hat{x}(t,\gamma)]\hat{\lambda}(t,\gamma)&=0,\\h[\hat{x}(t,\gamma)]+t+\gamma\lambda^*-\gamma\hat\lambda(t,\gamma)&=0.\end{aligned}
∇ f [ x ^ ( t , γ ) ] − ∇ h [ x ^ ( t , γ ) ] λ ^ ( t , γ ) h [ x ^ ( t , γ ) ] + t + γ λ ∗ − γ λ ^ ( t , γ ) = 0 , = 0 .
t
,
γ
t,\gamma
t , γ
[
∇
t
x
^
(
t
,
γ
)
T
∇
γ
x
^
(
t
,
γ
)
T
∇
t
λ
^
(
t
,
γ
)
T
∇
γ
λ
^
(
t
,
γ
)
T
]
=
A
(
t
,
γ
)
[
O
O
−
I
λ
^
(
t
,
γ
)
−
λ
∗
]
,
\begin{bmatrix}\nabla_t\hat x(t,\gamma)^T & \nabla_{\gamma}\hat x(t,\gamma)^T\\\nabla_t\hat\lambda(t,\gamma)^T & \nabla_{\gamma}\hat\lambda(t,\gamma)^T\end{bmatrix}=A(t,\gamma)\begin{bmatrix}O & O\\-I & \hat\lambda(t,\gamma)-\lambda^*\end{bmatrix},
[ ∇ t x ^ ( t , γ ) T ∇ t λ ^ ( t , γ ) T ∇ γ x ^ ( t , γ ) T ∇ γ λ ^ ( t , γ ) T ] = A ( t , γ ) [ O − I O λ ^ ( t , γ ) − λ ∗ ] ,
A
(
t
,
γ
)
=
[
∇
x
x
2
L
[
x
^
(
t
,
γ
)
,
λ
^
(
t
,
γ
)
]
−
∇
h
[
x
^
(
t
,
γ
)
]
∇
h
[
x
^
(
t
,
γ
)
]
T
−
γ
I
]
−
1
.
A(t,\gamma)=\begin{bmatrix}\nabla^2_{xx}\mathcal{L}[\hat x(t,\gamma),\hat\lambda(t,\gamma)] &- \nabla h[\hat x(t,\gamma)]\\\nabla h[\hat x(t,\gamma)]^T & -\gamma I\end{bmatrix}^{-1}.
A ( t , γ ) = [ ∇ x x 2 L [ x ^ ( t , γ ) , λ ^ ( t , γ ) ] ∇ h [ x ^ ( t , γ ) ] T − ∇ h [ x ^ ( t , γ ) ] − γ I ] − 1 .
∀
(
t
,
γ
)
:
∣
t
∣
<
δ
,
γ
∈
[
0
,
1
/
μ
ˉ
]
\forall(t,\gamma):|t|<\delta,\gamma\in[0,1/\bar\mu]
∀ ( t , γ ) : ∣ t ∣ < δ , γ ∈ [ 0 , 1 / μ ˉ ]
[
x
^
(
t
,
γ
)
−
x
∗
λ
^
(
t
,
γ
)
−
λ
∗
]
=
[
x
^
(
t
,
γ
)
−
x
^
(
0
,
0
)
λ
^
(
t
,
γ
)
−
λ
^
(
0
,
0
)
]
=
∫
0
1
A
(
ζ
t
,
ζ
γ
)
[
O
O
−
I
λ
^
(
ζ
t
,
ζ
γ
)
−
λ
∗
]
[
t
γ
]
 
d
ζ
.
\begin{aligned}\begin{bmatrix}\hat x(t,\gamma)-x^*\\\hat\lambda(t,\gamma)-\lambda^*\end{bmatrix}&=\begin{bmatrix}\hat x(t,\gamma)-\hat x(0,0)\\\hat\lambda(t,\gamma)-\hat\lambda(0,0)\end{bmatrix}\\&=\int_0^1A(\zeta t,\zeta\gamma)\begin{bmatrix}O & O\\-I & \hat\lambda(\zeta t,\zeta\gamma)-\lambda^*\end{bmatrix}\begin{bmatrix}t\\\gamma\end{bmatrix}\,\mathrm{d}\zeta.\end{aligned}
[ x ^ ( t , γ ) − x ∗ λ ^ ( t , γ ) − λ ∗ ] = [ x ^ ( t , γ ) − x ^ ( 0 , 0 ) λ ^ ( t , γ ) − λ ^ ( 0 , 0 ) ] = ∫ 0 1 A ( ζ t , ζ γ ) [ O − I O λ ^ ( ζ t , ζ γ ) − λ ∗ ] [ t γ ] d ζ .
γ
∈
[
0
,
1
/
μ
ˉ
]
\gamma\in[0,1/\bar\mu]
γ ∈ [ 0 , 1 / μ ˉ ]
δ
\delta
δ
A
(
t
,
γ
)
A(t,\gamma)
A ( t , γ )
{
(
t
,
γ
)
∣
∣
t
∣
<
δ
,
γ
∈
[
0
,
1
/
μ
ˉ
]
}
\{(t,\gamma)\mid|t|<\delta,\gamma\in[0,1/\bar\mu]\}
{ ( t , γ ) ∣ ∣ t ∣ < δ , γ ∈ [ 0 , 1 / μ ˉ ] }
M
ˉ
\bar M
M ˉ
∥
A
(
t
,
γ
)
∥
≤
M
ˉ
,
∀
∣
t
∣
<
δ
,
γ
∈
[
0
,
1
/
μ
ˉ
]
\Vert A(t,\gamma)\Vert\le\bar M,\forall|t|<\delta,\gamma\in[0,1/\bar\mu]
∥ A ( t , γ ) ∥ ≤ M ˉ , ∀ ∣ t ∣ < δ , γ ∈ [ 0 , 1 / μ ˉ ]
δ
\delta
δ
M
ˉ
δ
<
1
\bar M\delta<1
M ˉ δ < 1
(
∣
x
^
(
t
,
γ
)
−
x
∗
∣
2
+
∣
λ
^
(
t
,
γ
)
−
λ
∗
∣
2
)
1
/
2
≤
M
ˉ
(
∣
t
∣
+
max
0
≤
ζ
≤
1
∣
λ
^
(
ζ
t
,
ζ
γ
)
−
λ
∗
∣
γ
)
.
\begin{aligned}&\left(|\hat x(t,\gamma)-x^*|^2+|\hat\lambda(t,\gamma)-\lambda^*|^2\right)^{1/2}&\le\bar M\left(|t|+\max_{0\le\zeta\le1}|\hat\lambda(\zeta t,\zeta\gamma)-\lambda^*|\gamma\right).\end{aligned}
( ∣ x ^ ( t , γ ) − x ∗ ∣ 2 + ∣ λ ^ ( t , γ ) − λ ∗ ∣ 2 ) 1 / 2 ≤ M ˉ ( ∣ t ∣ + 0 ≤ ζ ≤ 1 max ∣ λ ^ ( ζ t , ζ γ ) − λ ∗ ∣ γ ) .
∀
(
t
,
γ
)
:
∣
t
∣
<
δ
,
γ
∈
[
0
,
1
/
μ
ˉ
]
,
γ
<
δ
\forall(t,\gamma):|t|<\delta,\gamma\in[0,1/\bar\mu],\gamma<\delta
∀ ( t , γ ) : ∣ t ∣ < δ , γ ∈ [ 0 , 1 / μ ˉ ] , γ < δ
∣
λ
^
(
t
,
γ
)
−
λ
∗
∣
≤
M
ˉ
∣
t
∣
+
M
ˉ
γ
max
0
≤
ζ
≤
1
∣
λ
^
(
ζ
t
,
ζ
γ
)
−
λ
∗
∣
.
|\hat\lambda(t,\gamma)-\lambda^*|\le\bar M|t|+\bar M\gamma\max_{0\le\zeta\le1}|\hat\lambda(\zeta t,\zeta\gamma)-\lambda^*|.
∣ λ ^ ( t , γ ) − λ ∗ ∣ ≤ M ˉ ∣ t ∣ + M ˉ γ 0 ≤ ζ ≤ 1 max ∣ λ ^ ( ζ t , ζ γ ) − λ ∗ ∣ .
t
,
γ
t,\gamma
t , γ
ζ
t
,
ζ
γ
,
ζ
∈
[
0
,
1
]
\zeta t,\zeta\gamma,\zeta\in[0,1]
ζ t , ζ γ , ζ ∈ [ 0 , 1 ]
max
0
≤
ζ
≤
1
∣
λ
^
(
ζ
t
,
ζ
γ
)
−
λ
∗
)
∣
≤
M
ˉ
1
−
M
ˉ
γ
∣
t
∣
.
\max_{0\le\zeta\le1}|\hat\lambda(\zeta t,\zeta\gamma)-\lambda^*)|\le\frac{\bar M}{1-\bar M\gamma}|t|.
0 ≤ ζ ≤ 1 max ∣ λ ^ ( ζ t , ζ γ ) − λ ∗ ) ∣ ≤ 1 − M ˉ γ M ˉ ∣ t ∣ .
∀
(
t
,
γ
)
:
∣
t
∣
<
δ
,
γ
∈
[
0
,
1
/
μ
ˉ
]
,
γ
<
δ
\forall(t,\gamma):|t|<\delta,\gamma\in[0,1/\bar\mu],\gamma<\delta
∀ ( t , γ ) : ∣ t ∣ < δ , γ ∈ [ 0 , 1 / μ ˉ ] , γ < δ
(
∣
x
^
(
t
,
γ
)
−
x
∗
∣
2
+
∣
λ
^
(
t
,
,
γ
)
−
λ
∗
∣
2
)
1
/
2
≤
(
μ
+
μ
2
γ
1
−
μ
γ
)
∣
t
∣
≤
M
ˉ
1
−
M
ˉ
δ
∣
t
∣
.
\left(|\hat x(t,\gamma)-x^*|^2+|\hat\lambda(t,,\gamma)-\lambda^*|^2\right)^{1/2}\le\left(\mu+\frac{\mu^2\gamma}{1-\mu\gamma}\right)|t|\le\frac{\bar M}{1-\bar M\delta}|t|.
( ∣ x ^ ( t , γ ) − x ∗ ∣ 2 + ∣ λ ^ ( t , , γ ) − λ ∗ ∣ 2 ) 1 / 2 ≤ ( μ + 1 − μ γ μ 2 γ ) ∣ t ∣ ≤ 1 − M ˉ δ M ˉ ∣ t ∣ .
δ
\delta
δ
(
∣
x
^
(
t
,
γ
)
−
x
∗
∣
2
+
∣
λ
^
(
t
,
,
γ
)
−
λ
∗
∣
2
)
1
/
2
≤
2
M
ˉ
∣
t
∣
.
\left(|\hat x(t,\gamma)-x^*|^2+|\hat\lambda(t,,\gamma)-\lambda^*|^2\right)^{1/2}\le2\bar M|t|.
( ∣ x ^ ( t , γ ) − x ∗ ∣ 2 + ∣ λ ^ ( t , , γ ) − λ ∗ ∣ 2 ) 1 / 2 ≤ 2 M ˉ ∣ t ∣ .
t
t
t
x
(
λ
,
μ
)
=
x
^
(
t
,
γ
)
,
λ
~
(
λ
,
μ
)
=
λ
^
(
t
,
γ
)
x(\lambda,\mu)=\hat x(t,\gamma),\tilde\lambda(\lambda,\mu)=\hat\lambda(t,\gamma)
x ( λ , μ ) = x ^ ( t , γ ) , λ ~ ( λ , μ ) = λ ^ ( t , γ )
∀
(
λ
,
μ
)
:
∣
λ
−
λ
∗
∣
<
δ
μ
,
μ
>
max
{
μ
ˉ
,
1
/
δ
}
\forall(\lambda,\mu):|\lambda-\lambda^*|<\delta\mu,\mu>\max\{\bar\mu,1/\delta\}
∀ ( λ , μ ) : ∣ λ − λ ∗ ∣ < δ μ , μ > max { μ ˉ , 1 / δ }
∣
x
(
λ
,
μ
)
−
x
∗
∣
≤
2
M
ˉ
∣
λ
−
λ
∗
∣
/
μ
,
∣
λ
~
(
λ
,
μ
)
−
λ
∗
∣
≤
2
M
ˉ
∣
λ
−
λ
∗
∣
/
μ
.
|x(\lambda,\mu)-x^*|\le2\bar M|\lambda-\lambda^*|/\mu,\quad|\tilde\lambda(\lambda,\mu)-\lambda^*|\le2\bar M|\lambda-\lambda^*|/\mu.
∣ x ( λ , μ ) − x ∗ ∣ ≤ 2 M ˉ ∣ λ − λ ∗ ∣ / μ , ∣ λ ~ ( λ , μ ) − λ ∗ ∣ ≤ 2 M ˉ ∣ λ − λ ∗ ∣ / μ .
M
=
2
M
ˉ
M=2\bar M
M = 2 M ˉ
∀
(
λ
,
μ
)
:
∣
λ
−
λ
∗
∣
<
δ
μ
,
μ
>
max
{
μ
ˉ
,
1
/
δ
}
\forall(\lambda,\mu):|\lambda-\lambda^*|<\delta\mu,\mu>\max\{\bar\mu,1/\delta\}
∀ ( λ , μ ) : ∣ λ − λ ∗ ∣ < δ μ , μ > max { μ ˉ , 1 / δ }
x
(
⋅
,
⋅
)
x(\cdot,\cdot)
x ( ⋅ , ⋅ )
M
M
M
∀
(
λ
,
μ
)
:
∣
λ
−
λ
∗
∣
<
δ
μ
,
≤
ˉ
μ
≤
max
{
μ
ˉ
,
1
/
δ
}
\forall(\lambda,\mu):|\lambda-\lambda^*|<\delta\mu,\bar\le\mu\le\max\{\bar\mu,1/\delta\}
∀ ( λ , μ ) : ∣ λ − λ ∗ ∣ < δ μ , ≤ ˉ μ ≤ max { μ ˉ , 1 / δ }
此定理解释了增广Lagrange函数法的一些显著的性质.
∥
x
k
−
x
∗
∥
≤
M
∥
λ
k
−
λ
∗
∥
/
μ
k
\Vert x_k-x^*\Vert\le M\Vert\lambda^k-\lambda^*\Vert/\mu_k
∥ x k − x ∗ ∥ ≤ M ∥ λ k − λ ∗ ∥ / μ k
λ
k
\lambda^k
λ k
μ
k
\mu_k
μ k
x
k
x_k
x k
x
∗
x^*
x ∗
x
k
x_k
x k
μ
k
\mu_k
μ k
∥
λ
k
+
1
−
λ
∗
∥
≤
M
∥
λ
k
−
λ
∗
∥
/
μ
k
\Vert\lambda^{k+1}-\lambda^*\Vert\le M\Vert\lambda^k-\lambda^*\Vert/\mu_k
∥ λ k + 1 − λ ∗ ∥ ≤ M ∥ λ k − λ ∗ ∥ / μ k
μ
k
\mu_k
μ k 无约束极小的二阶充分条件在第
k
k
k
本节我们讨论实用的增广Lagrange函数法, 特别地, 是要处理带不等式约束 的情形. 我们分别讨论三种方式——界约束重构、约束线性化重构和无约束重构 .
给定一般的非线性规划问题, 我们可以增加松弛变量
s
i
s_i
s i
c
i
(
x
)
−
s
i
=
0
,
s
i
≥
0
,
∀
i
∈
I
.
c_i(x)-s_i=0,\quad s_i\ge0,\quad\forall i\in\mathcal{I}.
c i ( x ) − s i = 0 , s i ≥ 0 , ∀ i ∈ I .
l
≤
x
≤
u
l\le x\le u
l ≤ x ≤ u
min
x
∈
R
n
f
(
x
)
,
s
u
b
j
e
c
t
 
t
o
 
c
i
(
x
)
=
0
,
i
=
1
,
2
,
…
,
m
,
l
≤
x
≤
u
.
\min\limits_{x\in\mathbb{R}^n}f(x),\quad\mathrm{subject\,to\,}c_i(x)=0,i=1,2,\ldots,m,l\le x\le u.
x ∈ R n min f ( x ) , s u b j e c t t o c i ( x ) = 0 , i = 1 , 2 , … , m , l ≤ x ≤ u .
l
l
l
−
∞
-\infty
− ∞
u
u
u
界约束重构的增广Lagrange函数法the bound-constrained Lagrangian methods, BCL methods 只包含等式约束, 即
L
A
(
x
,
λ
;
μ
)
=
f
(
x
)
−
∑
i
=
1
m
λ
i
c
i
(
x
)
+
μ
2
∑
i
=
1
m
c
i
2
(
x
)
.
\mathcal{L}_A(x,\lambda;\mu)=f(x)-\sum_{i=1}^m\lambda_ic_i(x)+\frac{\mu}{2}\sum_{i=1}^mc_i^2(x).
L A ( x , λ ; μ ) = f ( x ) − i = 1 ∑ m λ i c i ( x ) + 2 μ i = 1 ∑ m c i 2 ( x ) .
min
x
L
A
(
x
,
λ
;
μ
)
,
s
u
b
j
e
c
t
 
t
o
 
≤
x
≤
u
.
\min_x\mathcal{L}_A(x,\lambda;\mu),\quad\mathrm{subject\,to\,}\le x\le u.
x min L A ( x , λ ; μ ) , s u b j e c t t o ≤ x ≤ u .
λ
\lambda
λ
μ
\mu
μ
一种求解带界约束重构非线性规划的技术是非线性投影梯度法 , 可见下一章. 考虑子问题的KKT条件, 我们会发现
x
x
x
x
−
P
(
x
−
∇
x
L
A
(
x
,
λ
;
μ
)
,
l
,
u
)
=
0
,
x-P(x-\nabla_x\mathcal{L}_A(x,\lambda;\mu),l,u)=0,
x − P ( x − ∇ x L A ( x , λ ; μ ) , l , u ) = 0 ,
P
(
g
,
l
,
u
)
P(g,l,u)
P ( g , l , u )
g
∈
R
n
g\in\mathbb{R}^n
g ∈ R n
[
l
,
u
]
[l,u]
[ l , u ]
P
(
g
,
l
,
u
)
i
=
{
l
i
,
g
i
≤
l
i
,
g
i
,
g
i
∈
(
l
i
,
u
i
)
,
u
i
,
g
i
≥
u
i
,
i
=
1
,
2
,
…
,
n
.
P(g,l,u)_i=\left\{\begin{array}{ll}l_i, & g_i\le l_i,\\g_i, & g_i\in(l_i,u_i),\\u_i, & g_i\ge u_i,\end{array}\right.i=1,2,\ldots,n.
P ( g , l , u ) i = ⎩ ⎨ ⎧ l i , g i , u i , g i ≤ l i , g i ∈ ( l i , u i ) , g i ≥ u i , i = 1 , 2 , … , n .
算法4 (Bound-Constrained Lagrangian Method)
x
0
x_0
x 0
λ
0
\lambda^0
λ 0
η
∗
\eta_*
η ∗
w
∗
w_*
w ∗
μ
0
=
10
,
w
0
=
1
μ
0
,
η
0
=
1
/
μ
0
0.1
\mu_0=10,w_0=1\mu_0,\eta_0=1/\mu_0^{0.1}
μ 0 = 1 0 , w 0 = 1 μ 0 , η 0 = 1 / μ 0 0 . 1
k
=
0
,
1
,
2
,
…
k=0,1,2,\ldots
k = 0 , 1 , 2 , …
\quad\quad
x
k
x_k
x k
∥
x
k
−
P
(
x
k
−
∇
x
L
A
(
x
k
,
λ
k
;
μ
k
)
,
l
,
u
)
∥
≤
w
k
;
\Vert x_k-P(x_k-\nabla_x\mathcal{L}_A(x_k,\lambda^k;\mu_k),l,u)\Vert\le w_k;
∥ x k − P ( x k − ∇ x L A ( x k , λ k ; μ k ) , l , u ) ∥ ≤ w k ;
\quad\quad
∥
c
(
x
k
)
∥
≤
η
k
\Vert c(x_k)\Vert\le\eta_k
∥ c ( x k ) ∥ ≤ η k
\quad\quad\quad\quad
test for convergence )
\quad\quad\quad\quad
∥
c
(
x
k
)
∥
≤
η
∗
\Vert c(x_k)\Vert\le\eta_*
∥ c ( x k ) ∥ ≤ η ∗
∥
x
k
−
P
(
x
k
−
∇
x
L
A
(
x
k
,
λ
k
;
μ
k
)
,
l
,
u
)
∥
≤
w
∗
\Vert x_k-P(x_k-\nabla_x\mathcal{L}_A(x_k,\lambda^k;\mu_k),l,u)\Vert\le w_*
∥ x k − P ( x k − ∇ x L A ( x k , λ k ; μ k ) , l , u ) ∥ ≤ w ∗
\quad\quad\quad\quad\quad\quad
x
k
x_k
x k
\quad\quad\quad\quad
\quad\quad\quad\quad
update multipliers, tighten tolerances )
\quad\quad\quad\quad
λ
k
+
1
=
λ
k
−
μ
k
c
(
x
k
)
\lambda^{k+1}=\lambda^k-\mu_kc(x_k)
λ k + 1 = λ k − μ k c ( x k )
\quad\quad\quad\quad
μ
k
+
1
=
μ
k
\mu_{k+1}=\mu_k
μ k + 1 = μ k
\quad\quad\quad\quad
η
k
+
1
=
η
k
/
μ
k
+
1
0.9
\eta_{k+1}=\eta_k/\mu_{k+1}^{0.9}
η k + 1 = η k / μ k + 1 0 . 9
\quad\quad\quad\quad
w
k
+
1
=
w
k
/
μ
k
+
1
w_{k+1}=w_k/\mu_{k+1}
w k + 1 = w k / μ k + 1
\quad\quad
\quad\quad\quad\quad
increase penalty parameter, tighten tolerances )
\quad\quad\quad\quad
λ
k
+
1
=
λ
k
\lambda^{k+1}=\lambda^k
λ k + 1 = λ k
\quad\quad\quad\quad
μ
k
+
1
=
100
μ
k
\mu_{k+1}=100\mu_k
μ k + 1 = 1 0 0 μ k
\quad\quad\quad\quad
η
k
+
1
=
1
/
μ
k
+
1
0.1
\eta_{k+1}=1/\mu_{k+1}^{0.1}
η k + 1 = 1 / μ k + 1 0 . 1
\quad\quad\quad\quad
w
k
+
1
=
1
/
μ
k
+
1
w_{k+1}=1/\mu_{k+1}
w k + 1 = 1 / μ k + 1
\quad\quad
算法主要分岔位于近似求解子问题后, 算法将验证约束违反是否充分下降, 即验证条件
∥
c
(
x
k
)
∥
≤
η
k
.
\Vert c(x_k)\Vert\le\eta_k.
∥ c ( x k ) ∥ ≤ η k .
w
k
,
η
k
w_k,\eta_k
w k , η k
算法4中出现的常数0.1,0.9,100在某种程度上可以任取. 软件LANCELOT使用带信赖域的投影梯度法 求解界约束非线性子问题. 此时, 投影梯度法构建增广Lagrange函数
L
A
\mathcal{L}_A
L A 二次模型 , 并通过近似求解以下信赖域问题得到迭代步
d
d
d
min
d
1
2
d
T
[
∇
x
x
2
L
(
x
k
,
λ
k
)
+
μ
k
A
k
T
A
k
]
d
+
∇
x
L
A
(
x
k
,
λ
k
;
μ
k
)
T
d
s
u
b
j
e
c
t
 
t
o
l
≤
x
k
+
d
≤
u
,
∥
d
∥
∞
≤
Δ
,
\begin{array}{rl}\min\limits_d & \frac{1}{2}d^T\left[\nabla^2_{xx}\mathcal{L}(x_k,\lambda^k)+\mu_kA_k^TA_k\right]d+\nabla_x\mathcal{L}_A(x_k,\lambda^k;\mu_k)^Td\\\mathrm{subject\,to} & l\le x_k+d\le u,\quad\Vert d\Vert_{\infty}\le\Delta,\end{array}
d min s u b j e c t t o 2 1 d T [ ∇ x x 2 L ( x k , λ k ) + μ k A k T A k ] d + ∇ x L A ( x k , λ k ; μ k ) T d l ≤ x k + d ≤ u , ∥ d ∥ ∞ ≤ Δ ,
A
k
=
A
(
x
k
)
A_k=A(x_k)
A k = A ( x k )
Δ
\Delta
Δ
−
Δ
e
≤
d
≤
Δ
e
-\Delta e\le d\le\Delta e
− Δ e ≤ d ≤ Δ e
第一阶段, 做投影梯度线搜索以决定
d
d
d
第二阶段, 使用CG极小化子问题, 其中不再牵涉第一阶段中被固定的分量.
这有点类似于第十六章 二次规划的投影梯度法. 第二阶段相当于在可行多面体的某个面上做的极小化. 这一算法的好处在于, 无需计算KKT矩阵或者约束Jacobi矩阵
A
k
A_k
A k
需要说明的是, Lagrange函数的Hessian阵
∇
x
x
2
L
(
x
k
,
λ
k
)
\nabla^2_{xx}\mathcal{L}(x_k,\lambda^k)
∇ x x 2 L ( x k , λ k ) 部分可分结构 , 以高效计算Lagrange函数的Hessian阵或拟牛顿近似矩阵, 可见第七章 .
约束线性化重构的增广Lagrange函数法linearly constrained Lagragian methods, LCL methods 的主要想法是, 在线性化 原约束的限制下, 极小化Lagrange函数(或增广Lagrange函数), 产生迭代步. 对于上一小节中的一般非线性规划
min
x
∈
R
n
f
(
x
)
,
s
u
b
j
e
c
t
 
t
o
 
c
i
(
x
)
=
0
,
i
=
1
,
2
,
…
,
m
,
l
≤
x
≤
u
,
\min_{x\in\mathbb{R}^n}f(x),\quad\mathrm{subject\,to\,}c_i(x)=0,i=1,2,\ldots,m,l\le x\le u,
x ∈ R n min f ( x ) , s u b j e c t t o c i ( x ) = 0 , i = 1 , 2 , … , m , l ≤ x ≤ u ,
min
x
F
k
(
x
)
s
u
b
j
e
c
t
 
t
o
c
(
x
k
)
+
A
k
(
x
−
x
k
)
=
0
,
l
≤
x
≤
u
.
\begin{array}{rl}\min\limits_x & F_k(x)\\\mathrm{subject\,to} & c(x_k)+A_k(x-x_k)=0,\quad l\le x\le u.\end{array}
x min s u b j e c t t o F k ( x ) c ( x k ) + A k ( x − x k ) = 0 , l ≤ x ≤ u .
F
k
(
x
)
F_k(x)
F k ( x )
F
k
(
x
)
=
f
(
x
)
−
∑
i
=
1
m
λ
i
k
c
ˉ
i
k
(
x
)
,
F_k(x)=f(x)-\sum_{i=1}^m\lambda_i^k\bar{c}_i^k(x),
F k ( x ) = f ( x ) − i = 1 ∑ m λ i k c ˉ i k ( x ) ,
λ
k
\lambda^k
λ k
c
ˉ
i
k
(
x
)
\bar{c}_i^k(x)
c ˉ i k ( x )
c
i
(
x
)
c_i(x)
c i ( x )
x
k
x_k
x k 差函数 , 即
c
ˉ
i
k
(
x
)
=
c
i
(
x
)
−
c
i
(
x
k
)
−
∇
c
i
(
x
k
)
T
(
x
−
x
k
)
.
\bar{c}_i^k(x)=c_i(x)-c_i(x_k)-\nabla c_i(x_k)^T(x-x_k).
c ˉ i k ( x ) = c i ( x ) − c i ( x k ) − ∇ c i ( x k ) T ( x − x k ) .
x
k
x_k
x k
x
∗
x^*
x ∗ 对应于子问题中等式约束的Lagrange乘子将收敛于最优乘子 . 因此, 我们可设
λ
k
\lambda^k
λ k
现在LCL方法定义
F
k
F_k
F k
F
k
(
x
)
=
f
(
x
)
−
∑
i
=
1
m
λ
i
k
c
ˉ
i
k
(
x
)
+
μ
2
∑
i
=
1
m
[
c
ˉ
i
k
(
x
)
]
2
.
F_k(x)=f(x)-\sum_{i=1}^m\lambda_i^k\bar{c}_i^k(x)+\frac{\mu}{2}\sum_{i=1}^m[\bar c_i^k(x)]^2.
F k ( x ) = f ( x ) − i = 1 ∑ m λ i k c ˉ i k ( x ) + 2 μ i = 1 ∑ m [ c ˉ i k ( x ) ] 2 . 更好的全局收敛效果 .
可以看到, 上述
F
k
F_k
F k
c
i
(
x
)
c_i(x)
c i ( x )
c
ˉ
i
k
(
x
)
\bar c_i^k(x)
c ˉ i k ( x ) 仅捕捉
c
i
c_i
c i . 线性化约束重构子问题与原本的增广Lagrange函数子问题的不同则在于, 前者要求新迭代点
x
x
x
c
ˉ
i
k
\bar c_i^k
c ˉ i k
c
i
c_i
c i
μ
\mu
μ
因
c
ˉ
i
k
(
x
)
\bar c_i^k(x)
c ˉ i k ( x )
x
=
x
k
x=x_k
x = x k
∇
F
k
(
x
k
)
=
∇
f
(
x
k
)
\nabla F_k(x_k)=\nabla f(x_k)
∇ F k ( x k ) = ∇ f ( x k )
F
k
F_k
F k
MINOS包使用增广形式的模型函数, 用既约投影梯度法求解线性化子问题, 其中对
F
k
F_k
F k
利用近邻点proximal point 方法, 我们可以得到带不等式约束问题的无约束化重构增广Lagrange函数子问题. 为说明简便, 假设问题无等式约束, 于是我们可以将原问题等价地写作无约束优化问题
min
x
∈
R
n
F
(
x
)
,
\min\limits_{x\in\mathbb{R}^n}F(x),
x ∈ R n min F ( x ) ,
F
(
x
)
=
max
λ
≥
0
{
f
(
x
)
−
∑
i
∈
I
λ
i
c
i
(
x
)
}
=
{
f
(
x
)
,
x
 
i
s
 
f
e
a
s
i
b
l
e
,
∞
,
o
t
h
e
r
w
i
s
e
.
F(x)=\max_{\lambda\ge0}\left\{f(x)-\sum_{i\in\mathcal{I}}\lambda_ic_i(x)\right\}=\left\{\begin{array}{ll}f(x), & x\,is\,feasible,\\\infty, & otherwise.\end{array}\right.
F ( x ) = λ ≥ 0 max { f ( x ) − i ∈ I ∑ λ i c i ( x ) } = { f ( x ) , ∞ , x i s f e a s i b l e , o t h e r w i s e .
F
F
F
F
F
F
F
^
(
x
;
λ
k
,
μ
k
)
\hat F(x;\lambda^k,\mu_k)
F ^ ( x ; λ k , μ k )
F
F
F
μ
k
\mu_k
μ k
λ
k
\lambda^k
λ k
F
^
(
x
;
λ
k
,
μ
k
)
=
max
λ
≥
0
{
f
(
x
)
−
∑
i
∈
I
λ
i
c
i
(
x
)
−
1
2
μ
k
∑
i
∈
I
(
λ
i
−
λ
i
k
)
2
}
.
\hat F(x;\lambda^k,\mu_k)=\max_{\lambda\ge0}\left\{f(x)-\sum_{i\in\mathcal{I}}\lambda_ic_i(x)-\frac{1}{2\mu_k}\sum_{i\in\mathcal{I}}(\lambda_i-\lambda_i^k)^2\right\}.
F ^ ( x ; λ k , μ k ) = λ ≥ 0 max { f ( x ) − i ∈ I ∑ λ i c i ( x ) − 2 μ k 1 i ∈ I ∑ ( λ i − λ i k ) 2 } .
λ
\lambda
λ
λ
k
\lambda^k
λ k 它会使新的乘子
λ
\lambda
λ
λ
k
\lambda^k
λ k . 因
F
^
\hat F
F ^
λ
\lambda
λ 显式解
λ
i
=
{
0
,
−
c
i
(
x
)
+
λ
i
k
/
μ
k
≤
0
,
λ
i
k
−
μ
k
c
i
(
x
)
,
o
t
h
e
r
w
i
s
e
.
\lambda_i=\left\{\begin{array}{ll}0, & -c_i(x)+\lambda_i^k/\mu_k\le0,\\\lambda_i^k-\mu_kc_i(x), & otherwise.\end{array}\right.
λ i = { 0 , λ i k − μ k c i ( x ) , − c i ( x ) + λ i k / μ k ≤ 0 , o t h e r w i s e .
F
^
\hat F
F ^
F
^
(
x
;
λ
k
,
μ
k
)
=
f
(
x
)
+
∑
i
∈
I
ψ
(
c
i
(
x
)
,
λ
i
k
;
μ
k
)
,
\hat F(x;\lambda^k,\mu_k)=f(x)+\sum_{i\in\mathcal{I}}\psi(c_i(x),\lambda_i^k;\mu_k),
F ^ ( x ; λ k , μ k ) = f ( x ) + i ∈ I ∑ ψ ( c i ( x ) , λ i k ; μ k ) ,
ψ
\psi
ψ
ψ
(
t
,
σ
;
μ
)
=
d
e
f
{
−
σ
t
+
μ
2
t
2
,
t
−
σ
/
μ
≤
0
,
−
1
2
μ
σ
2
,
o
t
h
e
r
w
i
s
e
.
\psi(t,\sigma;\mu)\xlongequal{def}\left\{\begin{array}{ll}-\sigma t+\frac{\mu}{2}t^2, & t-\sigma/\mu\le0,\\-\frac{1}{2\mu}\sigma^2, & otherwise.\end{array}\right.
ψ ( t , σ ; μ ) d e f
{ − σ t + 2 μ t 2 , − 2 μ 1 σ 2 , t − σ / μ ≤ 0 , o t h e r w i s e .
x
x
x
F
^
(
x
;
λ
k
,
μ
k
)
\hat F(x;\lambda^k,\mu_k)
F ^ ( x ; λ k , μ k )
x
k
x_k
x k
F
F
F
L
A
\mathcal{L}_A
L A 向不等式约束情形的推广 . 不过, 由于其性质还未得到验证, 此无约束化重构并不如界约束重构和约束线性化重构一般, 具有常用软件包的内嵌.
在约束数目较小时, 人们通常使用二次罚函数法 . 事实上, 有时仅需对一个较大的
μ
\mu
μ
Q
(
x
;
μ
)
Q(x;\mu)
Q ( x ; μ )
μ
\mu
μ
尽管二次罚函数更直观、简洁, 但第3节与第4节的增广Lagrange函数法通常更受青睐 . 子问题的求解通常并不太难, 且乘子估计的引入避免了病态子问题的出现. 不过二次罚函数仍然作为许多算法正则化(regularization)的一种重要手段 , 譬如SQP.
一般情形的
l
1
l_1
l 1
l
1
l_1
l 1
l
1
l_1
l 1
近些年
l
1
l_1
l 1 被成功用于求解一些困难的问题 , 例如带互补约束的数学规划(mathematical programs with complementarity constraints, MPCCs), 其中约束不满足标准的约束规范. 将这些问题约束吸收为罚项而不是线性化, 之后后再使用诸如SQP或内点法, 我们能够扩展这些其他方法的应用面 . 软件包SNOPT在SQP算法中使用
l
1
l_1
l 1 防护策略 , 以防二次模型不可行或无界, 亦或有无界乘子.
增广Lagrange函数法由于其简洁性, 已受多年关注. MINOS和LANCELOT则是实施增广Lagrange函数法最好的软件包 . 它们也适用于大型非线性规划问题. 一般层面上, MINOS的LCL和LANCELOT的BCL有共同的性质. 但它们在计算迭代步的子问题和求解子问题的技术上具有较大差异:
MINOS使用既约空间法处理线性化约束, 并且使用(稠密)拟牛顿近似代替Lagrange函数的Hessian. 因此, MINOS对具有较小自由度的问题是最合适的 .
LANCELOT则更适用于约束较少的情形 . 正如第4节所说, LANCELOT无需约束Jacobi矩阵
A
A
A PENNON软件包也基于增广Lagrange函数法, 它在处理半定矩阵约束时较有优势 .
界约束重构和无约束重构Lagrange函数法的缺陷是, 它们增加了约束的平方, 让问题变得更复杂 . 这时, 我们只有通过极小化增广Lagrange函数才能获得可行性的改善 . 相反, LCL则在约束上计算牛顿类的迭代步, 稳步改善可行性 . 因此, 不难预见, 在带线性约束的问题上MINOS比LANCELOT更具优势 .
从第3节的增广Lagrange函数也可构造光滑精确罚函数(smooth exact penalty functions) , 但这些就过于复杂了. 例如我们提过等式约束的Fletcher光滑精确罚函数:
ϕ
F
(
x
;
μ
)
=
f
(
x
)
−
λ
(
x
)
T
c
(
x
)
+
μ
2
∑
i
∈
E
c
i
(
x
)
2
.
\phi_F(x;\mu)=f(x)-\lambda(x)^Tc(x)+\frac{\mu}{2}\sum_{i\in\mathcal{E}}c_i(x)^2.
ϕ F ( x ; μ ) = f ( x ) − λ ( x ) T c ( x ) + 2 μ i ∈ E ∑ c i ( x ) 2 .
λ
(
x
)
\lambda(x)
λ ( x )
λ
(
x
)
=
[
A
(
x
)
A
(
x
)
T
]
−
1
A
(
x
)
∇
f
(
x
)
=
(
A
T
)
†
∇
f
(
x
)
.
\lambda(x)=[A(x)A(x)^T]^{-1}A(x)\nabla f(x)=\left(A^T\right)^{\dagger}\nabla f(x).
λ ( x ) = [ A ( x ) A ( x ) T ] − 1 A ( x ) ∇ f ( x ) = ( A T ) † ∇ f ( x ) .
ϕ
F
\phi_F
ϕ F
ϕ
F
\phi_F
ϕ F
λ
(
x
)
\lambda(x)
λ ( x )
A
(
x
)
A(x)
A ( x )
λ
(
x
)
\lambda(x)
λ ( x )
A
(
x
)
A(x)
A ( x )
λ
\lambda
λ