同余和逆元
本篇博客将介绍同余和逆元,以及求逆元的三种方法(因为快速幂是本菜鸡在很久之前c语言还没学完的时候扣了一晚上看懂了,所以默认大家都会了)
放到一起总结一下。拖了好久的说。。。
然后,开始了。。。
同余
定义
给定一个正整数m,如果两个整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余,记作a≡b(mod m)。对模m同余是整数的一个等价关系。(百度百科)
换句话说,就是两个整数a和b对于m取模时的余数相等,称a和b对于模m同余。记作a≡b(mod m)。
举个栗子吧,比如:
6 | (47-35)成立,
因此47≡35(mod 6),分析一下就是47%6=5,35%6=5,满足余数相等,因此说47和35对模6同余。
然后放一些与同余有关的定理吧
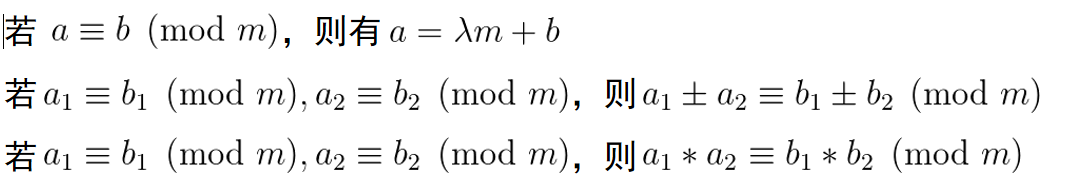
要注意的就是当除同余式的时候可能会出现错误。也就是说:
a1 * c ≡ b1 * c ( mod m )并不能得出a1 ≡ b1 ( mod m)这一关系式。
随时取模
下面说一个很有用的东西,也为了给后面的逆元做铺垫吧。这个很简单,大佬们可以直接跳过。
性质
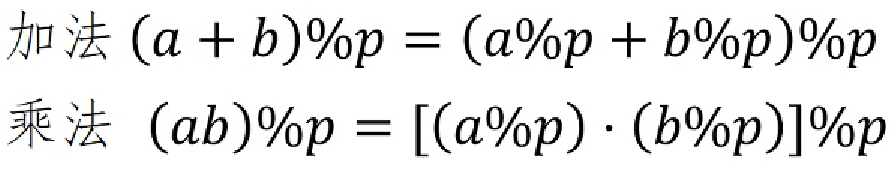
通过这个可以干很多事情,快速幂也用到了上面的两条性质。
这里举个不怎么 寻常的栗子吧,
我们很早之前就知道,如何判断一个数能否被三整除呢?
是的,将这个数的每一位相加,看所求的和能否被三整除,那么,我们现在就可以用上面的性质来证明这一规律。
假设现在有一个三位数qaq百位是a,十位是b,个位是c,即qaq=100 *a+10 *b+c。
然后我们将qaq对3进行取模可以得到:qaq%3=(100%3) *(a%3)+(10%3) *(b%3) + c%3,
然后继续化简可以得到: qaq%3=(a%3)+(b%3) +(c%3)=(a+b+c)%3
因此只有当(a+b+c)%3=0的时候,qaq才能被3整除,到此证毕。
然后迫不及待的小伙伴们可能发现了,上面的两条性质包括了加减和乘法,遇到除法我们该怎么进行随时取模的运算呢?
然后就引出了我们此篇博客的重点,逆元。
逆元
定义
它是一个可以取消另一给定元素运算的元素。
对于正整数a和m,如果有a*x≡1(mod m),那么把这个同余方程中x的最小正整数解叫做a模m的逆元。
思考了许久,先给一个前提吧,当然通用方法也会在后面附上。
前提
求a(modm)意义下的逆元,要求a与m互质,否则不存在乘法逆元
简单理解来说,就是化除法为乘法,举个栗子,当我们遇到a/b的时候,我们可以将其变为a*(1/b),也就是取倒数。只不过是在取模意义下的取倒数操作。
说起来很简单,但是实践起来还是一脸懵逼,本篇总结一下网上流传的三种常用方法吧。
(一)费马小定理求逆元
首先引入费马小定理:
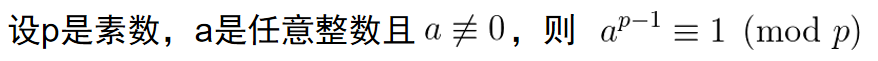
这给出定理的证明。(模大佬写博客法)
https://www.cnblogs.com/shandongs1/p/7759747.html

然后我们就可以利用这一定理求逆元了,很容易看出来
a(p-1) ≡ 1(mod p)可以变为a*a(p-2)≡ 1 (mod p)
此时a在模p意义下的逆元就很显然的能看出来了,是a(p-2),然后这个逆元我们就可以通过快速幂来求得,这是很简单很常用的一种方法。
代码(其实就是一个快速幂啦)
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
ll quickmi(ll a,ll b,ll p)
{
ll ans=1;
while(b)
{
if(b&1)ans=(ans*a)%p;
a=(a*a)%p;
b=b/2;
}
return ans;
}
int main()
{
ll p,a;
cin>>a>>p;
ll inv=quickmi(a,p-2,p);
cout<<inv<<endl;
return 0;
}
(二)扩展欧几里得求逆元
上篇博客中总结了扩展欧几里得,其实就是为了给这里的求逆元提前铺垫一下。。。。
不怎么会扩展欧几里得小伙伴可以看这个(宣传自己的博客)
https://blog.csdn.net/weixin_43939618/article/details/87926442
我们根据逆元的定义可以知道,当a* x≡1(mod m),那么把这个同余方程中x的最小正整数解叫做a模m的逆元。其实我们就是要求x的最小正整数解,那么我们将这个同余方程变换一下,因为是在模m意义下的,所以我们在方程的左边加上任意倍数的m,方程都是成立的。
于是我们将方程变换一下,可以得到:
a* x + m* y ≡ 1(mod m),这个二次方程也是成立的,而在大前提下,我们知道a与m是互素(互质)的,因此1= gcd(a ,b),到这里我相信大家激动的发现了a* x + m* y = gcd(a ,b),这玩意我们可以用扩展欧几里得解出来,然后解出来的最小正整数解x就是我们要的逆元了,到这里感觉还算好理解。
代码(就是写个扩欧啦)
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
void exgcd(ll a,ll b,ll &x,ll &y)
{
if(!b)
{
x=1,y=0;
return ;
}
exgcd(b,a%b,x,y);
ll t=y;
y=x-(a/b)*y,x=t;
return ;
}
int main()
{
ll p,a,x,y;
cin>>a>>p;
exgcd(a,p,x,y);
cout<<(x+p)%p<<endl;
return 0;
}
要注意的是因为求得是最小的正整数解,而最后得到的x可能是负数,要处理一下。具体的扩欧求最小正整数解和最大正整数解会在后面陆陆续续的写的。(疯狂给自己挖坑)
然后,牛逼的来了。
(三)O(n)递推公式求逆元
首先要解释一下,这个方法适用于求解一个区间1到n(n<mod)内的逆元问题时,能节省大量时间。
直接给递推公式:
inv[i] = ( mod - mod / i ) * inv[mod%i] % mod
大佬证明的很详细了:
https://blog.csdn.net/whyorwhnt/article/details/19169035
代码
inv[0]=1,inv[1]=1;
for(int i=2;i<=n;i++)
{
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
}
然后再说个贼有用的,为后面刷组合数学专题做个铺垫(又挖坑了),在组合数学中,常要求一个区间内的阶乘逆元,我们也可以利用递推式来求。
其实原理很简单的,先求出1到n的阶乘 fac[n] 数组,然后利用费马小定理或者扩欧求出n!的逆元,然后重点来了,这个式子解释了一切,1/fac[i] = (1/fac[i+1] )*(i+1),转换成逆元就是我们的递推式了,只不过这个递推是从后往前推的:
inv[i] =inv[ i+1]*(i+1)%mod
代码
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
ll fac[10005],inv[10005];
ll quickpow(ll a,ll b,ll p)
{
ll ans=1;
while(b)
{
if(b%2==1)ans=(ans*a)%p;
a=(a*a)%p;
b/=2;
}
return ans;
}
void init(ll p,int n)
{
fac[1]=1;
for(int i=2;i<=n;i++)fac[i]=(fac[i-1]*i)%p;
inv[n]=quickpow(fac[n],p-2,p);
for(int i=n-1;i>=1;i--)
{
inv[i]=inv[i+1]*(i+1)%p;
}
return ;
}
int main()
{
ll mod,n;
cin>>mod>>n;
init(mod,n);
for(int i=1;i<=n;i++)cout<<fac[i]<<" ";
cout<<endl;
for(int i=1;i<=n;i++)cout<<inv[i]<<" ";
return 0;
}
其实递推式这一方法需要注意的地方就是n<mod这一点。节省了大量的时间,很高效。而前两种费马小定理和扩展欧几里得则是基础中的基础,是必须要掌握的东西。
终于算是搞懂了逆元的一些内容,路还有很长,加油!