SMO算法详解(Sequential Minimal Optimization)
写作背景:最近在学SVM算法,在看了一些资料后,发现:很多书籍(例如:《机器学习》)或资料在讲解SVM算法时,都只是讲到了为了计算方便,可以将SVM算法需要求解的原始问题转化为它的对偶问题,然后使用SMO算法求解对偶问题,但是却没有详细解释SMO算法的具体解法。在我苦恼之际,实验室师兄分享给我一篇讲得很好的博客,因此,我将在这里总结一下用于求解对偶问题的SMO算法的具体解法。
参考论文:Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines
该论文是Microsoft Research的John C.Platt在1998年针对对偶问题提出的解法:即SMO算法。
这一方法很快就成为最快的二次规划优化算法,特别是针对线性SVM和数据稀疏时性能更优。
参考博客1:支持向量机通俗导论(理解SVM的三层境界)
在该博客中,作者July对SVM算法进行了由浅入深的详细讲解。用作者自己的话说就是:
全文宏观上整体认识支持向量机(SVM)的概念和用处,
微观上深究部分定理的来龙去脉,证明及原理细节,力保逻辑清晰 & 通俗易懂。
在讲解SVM算法那一部分时,就是参考的上面的论文。
参考博客2:机器学习实战教程(八):支持向量机原理篇之手撕线性SVM
在该博客中,作者Jack Cui将SVM的原理讲解得很清楚,推荐大家都看看
1. 为什么要将原始问题转化为对偶问题?
主要有3个原因:
1.对偶问题将原始问题中的约束转为了对偶问题中的等式约束。
2.方便核函数的引入。
3.改变了问题的复杂度。由求特征向量w转化为求比例系数a。
在原始问题下,求解的复杂度与样本的维度有关,即w的维度。在对偶问题下,只与样本数量有关。
2. 怎么将原始问题转化为对偶问题?
2.1 背景
支持向量机(SVM)的基本数学模型为:
这里 是样本点的总个数,缩写s.t.表示"Subject to",是"使得满足"的意思。上述公式描述的是一个典型的不等式约束条件下的二次型函数优化问题,同时也是支持向量机的基本数学模型。
2.2 准备知识
我们已经得到支持向量机的基本数学模型,接下来的问题就是如何根据数学模型,求得我们想要的最优解(即最优决策超平面)。在学习求解方法之前,我们得知道一点,想用我下面讲述的求解方法有一个前提,就是我们的目标函数必须是凸函数。理解凸函数,我们还要先明确另一个概念,凸集。在凸几何中,凸集(convex set)是在凸组合下闭合的放射空间的子集。凸集的定义是:如果集合中任意2个元素连线上的点也在集合中,那么这个集合就是凸集。看下图可能更容易理解:

左右两图分别是两个不同的集合。
显然,上图中的左图是一个凸集,上图中的右图是一个非凸集。
凸函数的定义也是如此,其几何意义表示为:函数任意两点连线上的值大于对应自变量处的函数值。若这里凸集
即某个区间
,那么,设函数
为定义在区间
上的函数,若对
上的任意两点
,
和任意的实数
,
(0,1),总有:
则函数
称为
上的凸函数,当且仅当其上镜图(在函数图像上方的点集)为一个凸集。再看一幅图,也许更容易理解:
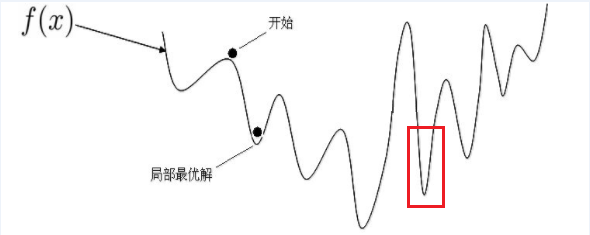
像上图这样的函数,它整体就是一个非凸函数,我们无法获得全局最优解的,只能获得局部最优解。比如红框内的部分,如果单独拿出来,它就是一个凸函数。对于我们的目标函数:
很显然,它是一个凸函数。所以,可以使用我接下来讲述的方法求取最优解。
通常我们需要求解的最优化问题有如下3类:
- (1)无约束优化问题,可以写为:
- (2)有等式约束的优化问题,可以写为:
- (3)有不等式约束的优化问题,可以写为:
对于第(1)类的优化问题,常常使用的方法就是费马大定理(Fermat),即使用求取函数f(x)的导数,然后令其为零,可以求得候选最优值,再在这些候选值中验证;如果是凸函数,可以保证是最优解。这也就是我们高中经常使用的求函数的极值的方法。
对于第(2)类的优化问题,常常使用的方法就是拉格朗日乘子法(Lagrange Multiplier) ,即把等式约束 用一个系数与 写为一个式子,称为拉格朗日函数,而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导,令其为零,可以求得候选值集合,然后验证求得最优值。
对于第(3)类的优化问题,常常使用的方法就是 条件。同样地,我们把所有的等式、不等式约束与 写为一个式子,也叫拉格朗日函数,系数也称拉格朗日乘子,通过一些条件,可以求出最优值的必要条件,这个条件称为 条件。
必要条件和充要条件如果不理解,可以看下面这句话:
- A的必要条件就是A可以推出的结论
- A的充分条件就是可以推出A的前提
显然,由于SVM的数学模型中有不等式约束条件,所以属于第(3)类优化问题。因此,在学习如何求解最优化问题之前,需先学习拉格朗日函数和KKT条件。
2.3 拉格朗日函数和KKT条件
2.3.1 拉格朗日函数
首先,我们先要从宏观的视野上了解一下拉格朗日对偶问题出现的原因和背景。
我们知道我们要求解的是最小化问题,所以一个直观的想法是如果我能够构造一个函数,使得该函数在可行解区域内与原目标函数完全一致,而在可行解区域外的数值非常大,甚至是无穷大,那么这个没有约束条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化问题是等价的问题。这就是使用拉格朗日方程的目的,它将约束条件放到目标函数中,从而将有约束优化问题转换为无约束优化问题。
随后,人们又发现,使用拉格朗日获得的函数,使用求导的方法求解依然困难。进而,需要对问题再进行一次转换,即使用一个数学技巧:拉格朗日对偶。
所以,显而易见的是,我们在拉格朗日优化我们的问题这个道路上,需要进行下面两个步骤:
- (第一步)将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数
- (第二步)使用拉格朗日对偶性,将不易求解的优化问题转化为易求解的优化问题
下面,进行第一步:将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数。
公式变形如下:
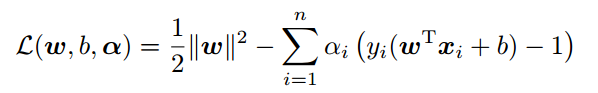
其中 是拉格朗日乘子, ,是我们构造新目标函数时引入的系数变量(我们自己设置)。现在我们令:

当样本点不满足约束条件时,即在可行解区域外:
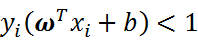
此时,我们将
设置为+
,此时
显然也是+
。
当样本点满足约束条件时,即在可行解区域内:

此时,显然 为原目标函数本身。我们将上述两种情况结合一下,就得到了新的目标函数:
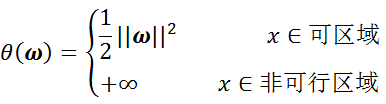
此时,再看我们的初衷,就是为了建立一个在可行解区域内与原目标函数相同,在可行解区域外函数值趋近于无穷大的新函数,现在我们做到了。
现在,我们的问题变成了求新目标函数的最小值,即:
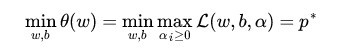
这里用 表示这个问题的最优值,且和最初的问题是等价的。
接下来,我们进行第二步:将不易求解的优化问题转化为易求解的优化问题。
我们看一下我们的新目标函数,先求最大值,再求最小值。这样的话,我们首先就要面对带有需要求解的参数 和 的方程,而 又是不等式约束,这个求解过程不好做。所以,我们需要使用拉格朗日函数对偶性,将最小和最大的位置交换一下,这样就变成了:
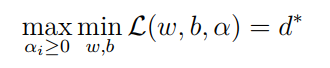
交换以后的新问题是原始问题的对偶问题,这个新问题的最优值用 来表示。而且 。我们关心的是 的时候,这才是我们要的解。需要满足以下两个条件才能让 。
- 首先必须满足这个优化问题是凸优化问题。
- 其次,需要满足KKT条件
凸优化问题的定义是:求取最小值的目标函数为凸函数的一类优化问题。目标函数是凸函数我们已经知道,这个优化问题又是求最小值。所以我们的最优化问题就是凸优化问题,即第一个条件已经满足。
接下里,就是探讨是否满足KKT条件了。
2.3.2 KKT条件
条件的全称是 条件, 条件是说对于以下数学模型:
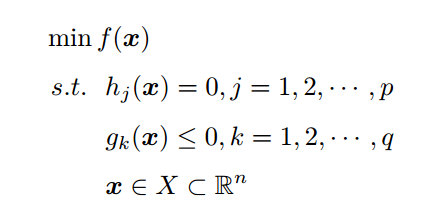
它的最优值条件必须满足以下条件:
- 条件一:经过拉格朗日函数处理之后的新目标函数L(w,b,α)对x求导为零:
- 条件二:h(x) = 0;
- 条件三:α*g(x) = 0;
对于SVM中求解的优化问题:显然满足以上三个条件,具体证明见:深入理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
从而,可以通过求解它的对偶问题来学习模型参数。
求解它的对偶学习问题,可以分为三个步骤:首先要让
关于
和
最小化,然后求对
的极大,最后利用SMO算法求解对偶问题中的拉格朗日乘子。
至此,使用SMO算法的背景以及准备知识已经讲解完毕,下面将会详细讲解SMO算法。
3. SMO算法的求解思路是什么?
思路:将大优化问题分解成多个小优化问题来求解。
步骤一
通过上面的推导,我们知道要求解的大优化问题,即对偶问题,为:

首先固定 ,要让 关于 和 最小化,我们分别对 和 偏导数,令其等于0,即:
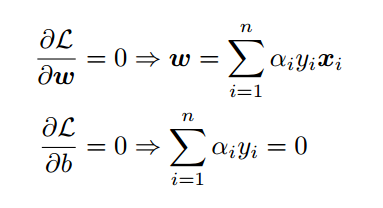
将上述结果带回 得到:
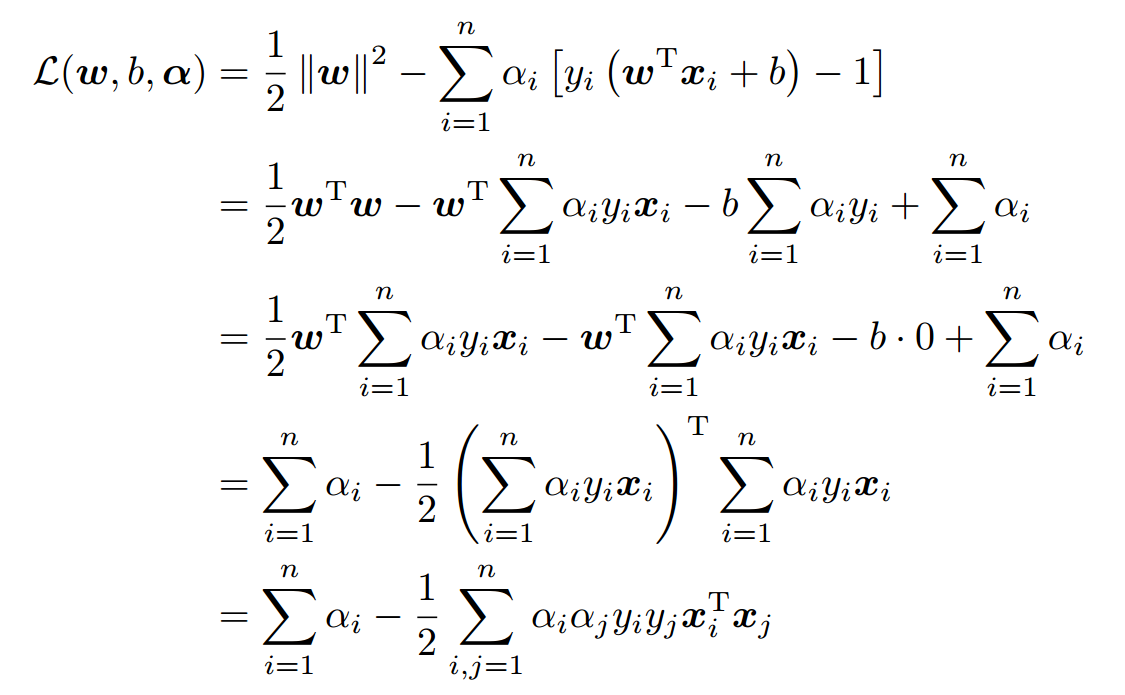
从上面的最后一个式子,我们可以看出,此时的 函数只含有一个变量,即 。
步骤二
现在内侧的最小值求解完成,我们求解外侧的最大值,从上面的式子得到:
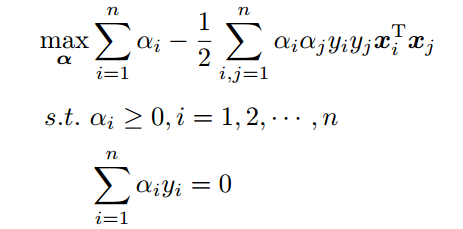
如上形式即为我们需要求解的最优化问题。
对于这个问题,我们用高效的优化算法,即SMO算法进行求解。通过SMO算法,首先得到
,再根据
,就可以求解出
和
,进而求得最初的目的:找到超平面,即"决策平面"。
具体地,SMO算法的工作原理为:每次循环中选择两个alpha进行优化处理。一旦找到了一对合适的alpha,那么就增大其中一个同时减小另一个。这里所谓的"合适"就是指两个alpha必须符合以下两个条件,条件之一就是两个alpha必须要在间隔边界之外,而且第二个条件则是这两个alpha还没有进行过区间化处理或者不在边界上。(后面会进行解释)
4. SMO的求解过程是怎样的?
将上一节中最后推导出的最优化问题,即目标函数前面加一个负号,将最大值问题转换成最小值问题:

实际上,对于上述目标函数,是存在一个假设的,即数据100%线性可分。但是,目前为止,我们知道几乎所有数据都不那么"干净"。这时我们就可以通过引入所谓的松弛变量 (slack variable)和惩罚参数 ,来允许有些数据点可以处于超平面的错误的一侧。此时我们的约束条件有所改变:

同时,考虑到松弛变量和松弛变量 和惩罚参数 ,目标函数变为:
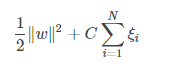
原始问题的拉格朗日函数变为:
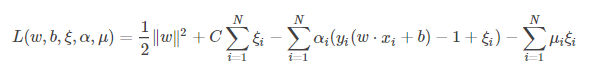
对偶问题拉格朗日函数的极大极小问题,得到以下等价优化问题:
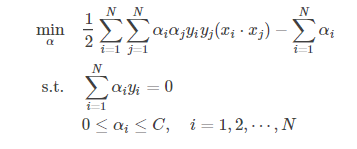
则,原始问题的解对偶问题的解相同需要满足KKT对偶互补条件,即:

对样本点 ,记SVM的输出结果为:

Platt在序列最小优化(SMO)方法1中提到,对正定二次优化问题(a positive definite QP problem)的优化点的充分必要条件为KKT条件(Karush-Kuhn-Tucker conditions)。
对于所有的
,若满足以下条件,QP问题可解。KKT条件如下:

其中 就是每个样本点的函数间隔。
KKT条件推导

因此推出:

而最优解需要满足KKT条件,即上述3个条件都得满足,如果存在不能满足KKT条件的 ,那么需要更新这些 ,这是第一个约束条件。此外,更新的同时还要受到第二个约束条件的限制,即:

因为这个条件,我们同时更新两个 值,因为只有成对更新,才能保证更新之后的值仍然满足和为0的约束,假设我们选择的两个乘子为 和 :
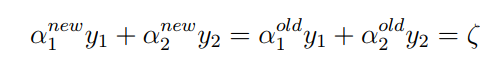
其中, 为常数。因为两个因子不好同时求解,所以可以先求第二个乘子 的解( ),得到 的解( )之后,再用 的解( )表示 的解( )。为了求解 ,得先确定 的取值范围。假设它的上下边界分别为 和 ,那么有:
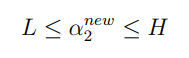
接下来,综合下面两个条件:
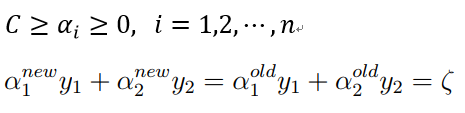
当 时,即一个为+1,一个为-1的时候,可以得到:
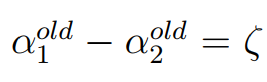
所以有:
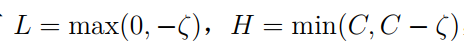
此时,取值范围如下图所示:

当 时,即两个都为+1或者都为-1,可以得到:

所以有:

此时,取值范围如下图所示:
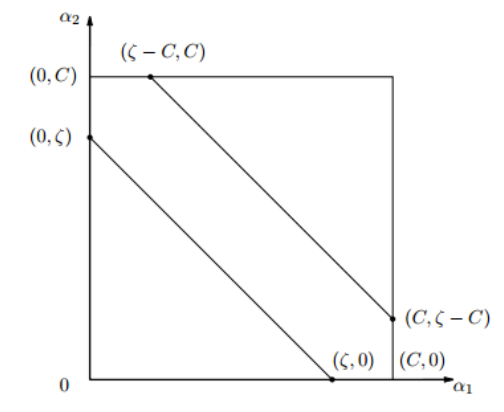
如此,根据 和 异号或同号,可以得出 的上下界分别为:
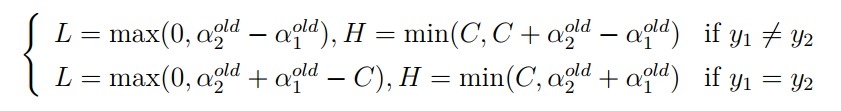
这个界限就是编程的时候需要用到的。已经确定了边界,接下来,就是推导迭代式,用于更新 值。
我们已经知道,更新 的边界,接下来就是讨论如何更新 值。我们依然假设选择的两个乘子为 和 。固定这两个乘子,进行推导。于是目标函数变成了:
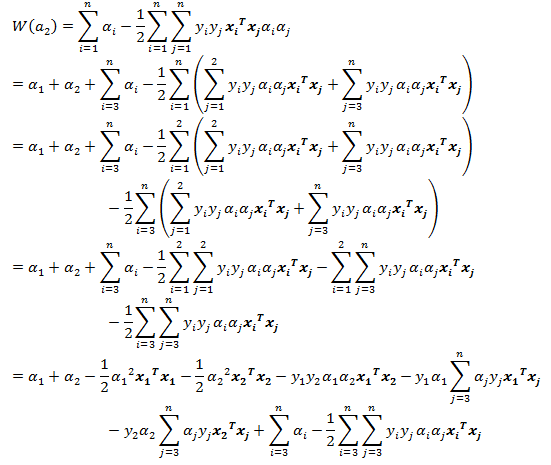
为了描述方便,我们定义如下符号:
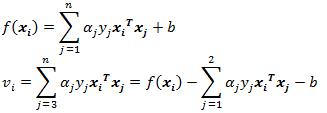
最终目标函数变为:
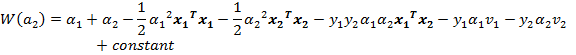
我们不关心 的部分,因为对于 和 来说,它们都是常数项,在求导的时候,直接变为0。对于这个目标函数,如果对其求导,还有个未知数 ,所以要推导出 和 的关系,然后用 代替 ,这样目标函数就剩一个未知数了,我们就可以求导了,推导出迭代公式。所以现在继续推导 和 的关系。注意第一个约束条件:

我们在求 和 的时候,可以将 , ,…, 和 , ,…, 看作常数项。因此有:
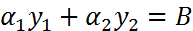
我们不必关心常数 的大小,现在将上述等式两边同时乘以 ,得到( ):
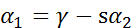
其中 为常数 ,我们不关心这个值, 。接下来,我们将得到的 带入 公式得:
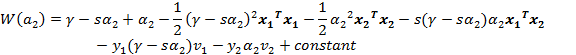
这样目标函数中就只剩下 了,我们对其求偏导(注意: ,所以 的平方为1, 的平方和 的平方均为1)

继续化简,将 带入方程得:
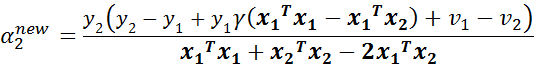
我们令:

为误差项, 为学习速率。
再根据我们已知的公式:
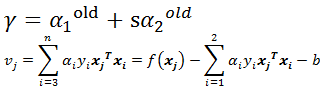
将 继续化简得:
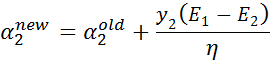
这样,我们就得到了最终需要的迭代公式。这个是没有经过剪辑的解,需要考虑约束:
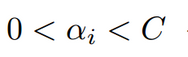
根据之前推导的 取值范围,我们得到最终的解析解为:

又因为:

消去 得:
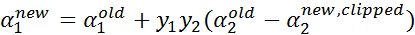
这样,我们就知道了怎样计算 和 了,也就是如何对选择的 进行更新。
当我们更新了 和 之后,需要重新计算阈值 ,因为 关系到了我们 的计算,也就关系到了误差 的计算。
我们要根据 的取值范围,去更正 的值,使间隔最大化。当 的时候,根据KKT条件可知,这个点是支持向量上的点。因此,满足下列公式:
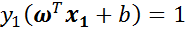
公式两边同时乘以 得( ):
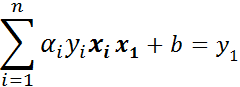
因为我们是根据 和 的值去更新 ,所以单独提出 和 的时候,整理可得:

其中前两项为:
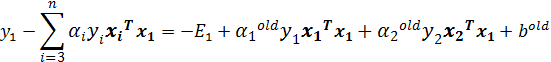
将上述两个公式,整理得:

同理可得 为:
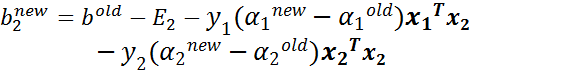
当 和 都有效的时候,它们是相等的,即:
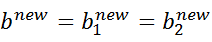
当两个乘子都在边界上,则 阈值和KKT条件一致。当不满足的时候, 算法选择他们的中点作为新的阈值:

最后,更新所有的 和 ,这样模型就出来了,从而即可求出我们的分类函数。
5. SMO算法的步骤总结
- 步骤1:计算误差 :
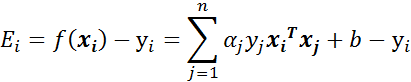
- 步骤2:计算上下界 和 :
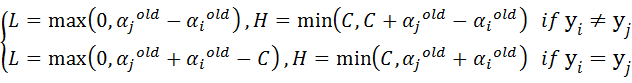
- 步骤3:计算 :
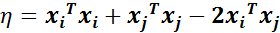
- 步骤4:更新 :
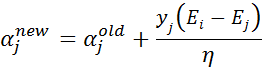
- 步骤5:根据取值范围修剪 :
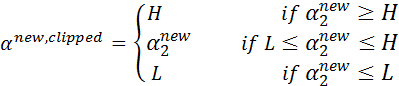
- 步骤6:更新 :

- 步骤7:更新 和 :
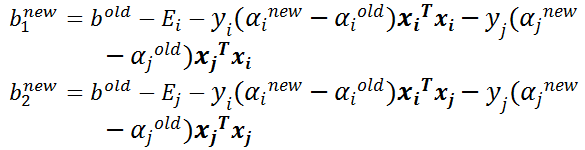
- 步骤8:根据 和 更新 :
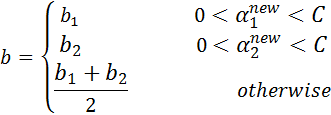
最后的最后(作者的话)
如果你看到了这里,那么你一个是一个很优秀的人(能这么有耐心地看完我写的这篇博客_)。由于我也是参考了很多博客后才写的这篇博客,所以地方我可能没有讲得很清楚,如果有任何问题留言,或者直接邮箱([email protected])与我私信交流。