机器学习模型自我代码复现：SVM(SMO算法)

根据模型的数学原理进行简单的代码自我复现以及使用测试，仅作自我学习用。模型原理此处不作过多赘述，仅罗列自己将要使用到的部分公式。

如文中或代码有错误或是不足之处，还望能不吝指正。

SVM是一种分类算法，其思路是：找出一个（超）平面，以此分割2个类别。满足这一要求的（超）平面有许多。我们还期望，2个类别中离超平面距离最近的那几个点到超平面的距离尽可能的大，使得分割效果更“明显”，效果更好，离超平面距离最近的那几个点被称为“支持向量”。

将上述语言转化为一个公式，就是希望找到

$min_{\omega,b}\frac{1}{2} ||\omega||^2$

$s.t. y_i(w^Tx_i+b>=1,i=1,2,...,m)$

其中， $f(x_i) = w^Tx_i+b$ 为对应超平面； $min_{\omega,b}\frac{1}{2} ||\omega||^2$ 为间隔最大化的等价条件，此处省略推导过程。对其使用拉格朗日乘子法，得

$L(\omega,b,\alpha)=\frac{1}{2}||\omega||^2 + \Sigma_{i=1}^m\alpha_i(1-y1(\omega^Tx_i+b))$ 其中，α_i为拉格朗日乘子。

同时满足KKT条件：

$\begin{equation} \left\{ \begin{array}{lr} \alpha_i>=0, & \\ y_if(x_i)-1>=0\\ \alpha_i(y_if(x_i)-1)=0 & \end{array} \right. \end{equation}$

对于拉格朗日乘子法的解而言，如果有某个点的拉格朗日乘子 $\alpha_i$ 不为0，就代表其是“支持向量”，实际只有它们是对最终结果产生影响的。

根据SMO算法的思想，我们每次首先选择一个违反KKT条件最严重的 $\alpha_i$ ，之后寻找一个与样本 $x_i$ 距离最远的样本 $x_j$ 对应的 $\alpha_j$ 。因为这2个变量有很大的差别，所以带给函数值的变化更大。

以下是 $\alpha_i$ $\alpha_j$ 的求解过程，笔者正在自行理解中，不再赘述推理过程。

$\eta = K_{ii} + K_{jj} - 2K_{ij} \\ E_i = (\Sigma_k\alpha_ky_kK_{ik}+b)-y_i \\ alpha_j^{*} = alpha_2^{old} + \frac{y_2(E_i-E_j)}{\eta}$

$\alpha_j^{new}= \begin{equation} \left\{ \begin{array}{lr} H , \alpha_j^*>H, & \\ \alpha_j^*,L<=\alpha_j^*<=H \\ L,\alpha_j^*<L & \end{array} \right. \end{equation}$

其中，当y_i=y_j时， $L = max(0,\alpha_j^{old}-\alpha_i^{old}) H = min(C,C+\alpha_j^{old}-\alpha_i^{old})$

当y_i!=y_j时 $L = max(0,\alpha_j^{old}-\alpha_i^{old}-C) H = min(C,\alpha_j^{old}+\alpha_i^{old})$

$\alpha_i^{new} = \alpha_i^{old}+y_iy_j(\alpha_j^{old}-\alpha_j^{new})$

同时更新偏置项b

$b1 = -E_i - y_i*(\alpha_i^{new}-\alpha_i^{old})*K_{ii}-y_jK_{ij}(\alpha_j^{new}-\alpha_j^{old})+b$

$b2 = -E_j - y_i*(\alpha_i^{new}-\alpha_i^{old})*K_{ij}-y_jK_{jj}(\alpha_j^{new}-\alpha_j^{old})+b$

当 $0<\alpha_i^{new}<C$ 时，取b=b1

当 $0<\alpha_j^{new}<C$ 时，取b=b2

同时满足以上条件时,b=b1=b2

否则取b = (b1+b2)/2

最终，

$W = \sum \alpha_iy_ix_i$

此处的代码参考了GitHub上的GitHub - xinlianghu/svm: 用Python实现SVM多分类器

应该是以《统计学习方法》为基础的代码。

import numpy as np
import pandas as pd
import random

class SVM:
    def __init__(self,data,labels,C,toler,gaussian_kernel=True) -> None:
        """
        初始化
        data:自变量
        labels:因变量
        C:软间隔的惩罚因子
        toler:偏离KKT条件的容错率
        gaussian_kernel:是否使用高斯核
        Es:误差缓存
        m:数据量
        b:偏置
        """
        self.kernel = gaussian_kernel
        self.data = data
        self.labels = labels
        self.C = C
        self.toler = toler
        self.gaussian_kernel = gaussian_kernel
        self.m = data.shape[0]
        self.alphas = np.zeros(self.m)
        self.Es = np.zeros((self.m,2)) #Ei是否有效 Ei当前值
        self.b = 0
        self.iter = 0
        
    def K(self,i,j,gamma = 1/2):
        """
        核函数计算，gaussian_kernel==False时默认为线性核函数
        """
        if self.gaussian_kernel:
            return np.exp(-gamma*np.linalg.norm(self.data[i,:]-self.data[j,:])**2)
        else:
            return sum(self.data[i,:]*self.data[j,:])
            

    def calc_Ek(self,k):
        """
        根据拉格朗日因子alpha与核函数计算第k个误差项
        """
        gxi = np.dot(self.alphas*self.labels,np.array([self.K(k,j) for j in range(self.m)]))+self.b
        return gxi-float(self.labels[k])

    def train(self,max_Iter):
        """
        训练
        此函数中首先选择alpha_i，之后再内循环中选择alpha_j
        max_Iter:最大迭代次数
        """
        last_changed = 0
        entrySet = True #是否遍历整个数据集
        last_changed = 0 #有几对alpha被改变了
        while self.iter<max_Iter and ((last_changed>0) or entrySet):
            last_changed = 0.0
            if entrySet:
                for i in range(self.m):
                    last_changed+=self.innerL(i)
                self.iter += 1
                entrySet = False
            else:
                nonBounds = np.nonzero((self.alphas>0)*(self.alphas<self.C))[0]
                for i in nonBounds:
                    last_changed+=self.innerL(i)
                self.iter+=1
                if last_changed==0:
                    entrySet = True
        #计算权重
        self.w = np.zeros((1,self.data.shape[1]))
        for i in range(self.m):
            if self.alphas[i]>0:
                self.w+=self.labels[i]*self.alphas[i]*self.data[i,:]
                
    
    def innerL(self,k):
        """
        内循环
        根据给定条件选定alpha_j,与之前的alpha_i一起更新
        """
        Ek = self.calc_Ek(k)
        last_changed = 0
        if (self.labels[k]*Ek < -self.toler and self.alphas[k]<self.C) or (self.labels[k]*Ek>self.toler and self.alphas[k]>0):
            self.Es[k] = [1,Ek]
            j,Ej = self.selectJ(k)
            res = self.update(k,j,Ek,Ej)
            last_changed+=res
        return last_changed
    
    def update(self,i,j,Ei,Ej):
        """
        更新alpha_i,alpha_j,b
        """
        #首先更新alpha_j
        if(self.labels[i]==self.labels[j]):
            L = max(0,self.alphas[j]+self.alphas[i]-self.C)
            H = min(self.C,self.alphas[j]+self.alphas[i])
        else:
            L = max(0,self.alphas[j]-self.alphas[i])
            H = min(self.C,self.C+self.alphas[j]-self.alphas[i])
        if L==H:
            return 0
            
        eta = self.K(i,i)+self.K(j,j)-2*self.K(i,j)
        if eta == 0: #这里不考虑eta（分母）==0的情况
            return 0
        origin_alpha_j = self.alphas[j].copy()
        origin_alpha_i = self.alphas[i].copy()
        self.alphas[j] = self.alphas[j]+self.labels[j]*(self.labels[j]*(Ei-Ej)/eta)
        if self.alphas[j]>H:
            self.alphas[j]=H
        elif self.alphas[j]<L:
            self.alphas[j]=L
        self.Es[j] = [1,self.calc_Ek(j)]
        if abs(self.alphas[j]-origin_alpha_j)<0.00001:
            return 0
        #更新alpha_i
        self.alphas[i] = self.alphas[i]+self.labels[i]*self.labels[j]*(origin_alpha_j-self.alphas[j])
        self.Es[i] = [1,self.calc_Ek(i)]
        #更新b
        bi = -self.Es[i][1]-self.labels[i]*(self.alphas[i]-origin_alpha_i)*self.K(i,i)-self.labels[j]*(self.alphas[j]-origin_alpha_j)*self.K(i,j)+self.b
        bj = -self.Es[j][1]-self.labels[i]*(self.alphas[i]-origin_alpha_i)*self.K(i,j)-self.labels[j]*(self.alphas[j]-origin_alpha_j)*self.K(j,j)+self.b
        print(self.Es[i][1],self.Es[j][1],self.alphas[i]-origin_alpha_i,self.alphas[j]-origin_alpha_j)
        if self.C>self.alphas[i] and self.alphas[i]>0:
            self.b = bi
        elif self.C>self.alphas[j] and self.alphas[j]>0:
            self.b = bj
        else:
            self.b = (bi+bj)/2.0
        return 1

    def selectJ(self,i):
        """
        根据i选择alpha_j
        """
        Ei = self.Es[i][1]
        maxdelta = 0
        j=0
        Ej = 0
        validEsList = np.nonzero(self.Es[:,0])[0]
        #初次循环时，随机选择一个j，之后循环选择误差相距的alpha_j
        if len(validEsList)>1:
            for k in validEsList:
                if k == i:
                    continue
                Ek = self.calc_Ek(k)
                delta = abs(Ei-Ek)
                if delta>maxdelta:
                    maxdelta = delta
                    j=k
                    Ej = Ek
        else:
            j = i
            while j==i:
                j = int(np.random.uniform(0,self.m))
            Ej = self.calc_Ek(j)
        return j,Ej

使用自造数据集进行检验

x1 = np.random.randn(100)*2+10
x2 = np.random.randn(100)*2+20
x3 = np.random.randn(100)*2+10
x4 = np.random.randn(100)*2+20

data = np.r_[np.c_[x1,x3],np.c_[x2,x4]]
labels = np.array([1]*100+[-1]*100)

svm = SVM(data,labels,C=0.225,toler=0.001,gaussian_kernel=False)
svm.train(max_Iter=40)

x_pre = np.linspace(5,25,200)
y_pre = -(svm.w[0][0] * x_pre + svm.b)/(svm.w[0][1])

from matplotlib import pyplot as plt
import matplotlib as mpl

mpl.rcParams["font.family"]="SimHei"
mpl.rcParams["axes.unicode_minus"]=False

plt.scatter(x1,x3)
plt.scatter(x2,x4)
plt.scatter(x_pre,y_pre)
plt.show()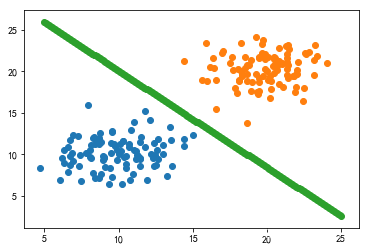

从图像上看，的确找到了能够分割2个类别的线。

但是，依然有2个问题存在：一是b的值似乎对惩罚数C十分敏感，从理论上来说不应该这样的。

二是我不是很理解Es矩阵中的“有效”概念。我的理解是，不能随意取Es，否则各个 $\alpha$ 都有机会大于0。关于这两点我还得再研究一下。

机器学习模型自我代码复现：SVM(SMO算法)

猜你喜欢