山东大学机器学习（实验二内容）——逻辑回归和牛顿法

版权声明：欢迎转载和交流。 https://blog.csdn.net/Hachi_Lin/article/details/86644759

1. 描述

在本练习中，您将使用牛顿方法对分类问题实现逻辑回归。

2.数据

  首先，下载data2.zip并从zip文件中提取文件。 在本练习中，假设一所高中有一个数据集，该数据集表示40名被大学录取的学生和40名未被录取的学生。 每个 $(x(i) ;y(i))$训练示例包含学生在两个标准化考试中的成绩以及学生是否被录取的标签。
  您的任务是建立一个二元分类模型，根据 学生在两门考试中的成绩来估计大学录取的机会。 在训练数据中， $x$数组的第一列代表所有测试1的分数，第二列代表所有测试2的分数， $y$矢量使用" 1“标记被录取的学生和" 0”标记 没被录取的学生。

3.绘制数据

  将训练样例的数据加载到程序中，并将 $x_0 = 1$截距项添加到 $x$矩阵中。
  在开始牛顿方法之前，我们将首先使用不同的符号绘制数据来表示两个类。 在Matlab / Octave中，您可以使用find命令分离正类和负类：

% find返回满足指定条件的行的索引
pos = find ( y == 1 ) ; neg = find ( y == 0 ) ;
% Assume the features are in the 2nd and 3rd columns of x
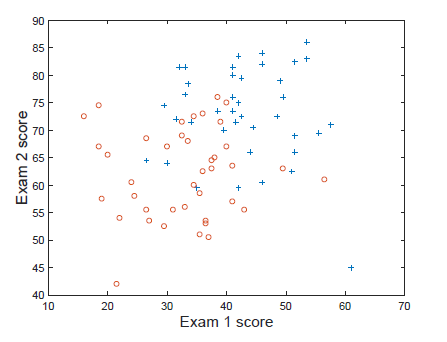
plot ( x ( pos , 2 ) , x ( pos , 3 ) , '+' ) ; hold on
plot ( x ( neg , 2 ) , x ( neg , 3 ) , ' o ' )

你画的应该如下所示

4 .逻辑回归

回想一下逻辑回归，假设函数为
$h _ { \theta } ( x ) = g \left( \theta ^ { T } x \right) = \frac { 1 } { 1 + e ^ { - \theta ^ { T } x } } = P ( y = 1 | x ; \theta ) \tag{1}$
Matlab/Octave没有sigmoid函数库，所以你必须自己定义它。最简单的方法是通过内联表达式。

g = inline('1.0 ./ (1.0 + exp(-z))');
%Usage: To find the value of sigmoid
%evaluated at 2, call g(2)

给定一个训练集 $\{x^{(i)}\}_{i=1,\dots,m}$我们定义一个极大似然函数为
$J ( \theta ) = \prod _ { i = 1 } ^ { m } \left( h _ { \theta } \left( x ^ { ( i ) } \right) \right) ^ { y ^ { ( i ) } } \left( 1 - h _ { \theta } \left( x ^ { ( i ) } \right) \right) ^ { 1 - y ^ { ( t ) } } \tag{2}$
为了便于计算，我们将下面的对数函数最大化
$L ( \theta ) = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left[ y ^ { ( i ) } \log \left( h _ { \theta } \left( x ^ { ( i ) } \right) \right) + \left( 1 - y ^ { ( i ) } \right) \log \left( 1 - h _ { \theta } \left( x ^ { ( i ) } \right) \right) \right] \tag{3}$
记住，最大化(3)等于最小化它的负数，然后我们的问题变成了
$\min _ { \theta } L ( \theta ) = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left[ - y ^ { ( i ) } \log \left( h _ { \theta } \left( x ^ { ( i ) } \right) \right) - \left( 1 - y ^ { ( i ) } \right) \log \left( 1 - h _ { \theta } \left( x ^ { ( i ) } \right) \right) \right] \tag{4}$
其中 $\nabla_\theta L$是 $L$的梯度，其定义如下
$\nabla _ { \theta } L = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left( h _ { \theta } \left( x ^ { ( i ) } \right) - y ^ { ( i ) } \right) x ^ { ( i ) } \tag{5}$
上述目标函数最小化的一种方法是梯度下降算法，我们根据以下规则更新迭代 $\theta$
$\theta \leftarrow \theta - \alpha \nabla _ { \theta } L ( \theta ) \tag{6}$
直到连续迭代的目标函数之间的差值小于(或等于)某个阈值，即
$\left| L ^ { + } ( \theta ) - L ( \theta ) \right| \leq \epsilon \tag{7}$
使用初始化 $\theta = 0$的梯度下降算法尝试解决逻辑回归的问题，并回答下列问题。

1. 假设 $\epsilon = 10 ^ { - 6 }$。实现收很慢敛需要多少次迭代？注意，梯度下降算法收敛速度，可能需要很长时间才能达到最小值。
2. 收敛后得到的 $\theta$值是多少？
3. 计算每次迭代过程中的 $L(\theta)$和说明 $L(\theta)$在梯度下降算法中如何减少。
4. 收敛之后，使用 $\theta$的值找出分类问题的决策边界。决策边界定义为其中的直线
   $P(y=1|x;\theta) = g(\theta^Tx) = 0.5$
   这对应于
   $\theta^Tx = 0$
   绘制边界相当于绘制 $\theta^Tx = 0$。当你完成时，你绘制应该如下图所示。注意，在不同的参数设置下，图可能略有不同。

5. 测试1的成绩为20分和测试2为80分的学生不被录取的概率是多少？

5. 牛顿方法

我们的目标是使用牛顿方法去最小化这个函数。回想一下牛顿方法的更新规则是
$\theta ^ { ( t + 1 ) } = \theta ^ { ( t ) } - H ^ { - 1 } \nabla _ { \theta } L$
在逻辑回归中，海森矩阵是
$H = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left[ h _ { \theta } \left( x ^ { ( i ) } \right) \left( 1 - h _ { \theta } \left( x ^ { ( i ) } \right) \right) x ^ { ( i ) } \left( x ^ { ( i ) } \right) ^ { T } \right] \tag{8}$
  注意，上面给出的公式是向量化的版本。具体来说，这意味着 $x^{(i)} \in R^{n+1}, x^{(i)}(x^{(i)})^T \in R^{(n+1) \times (n+1)}$，其中 $h_\theta(x^{(i)})$和 $y^{(i)}$是标量。
  现在，在你的程序中实现牛顿法，从初值 $\theta = 0$。使用和(7)相同的停止条件的梯度下降算法。为了确定使用多少迭代，计算每次迭代过程中的 $L(\theta)$和绘制你的结果。牛顿方法通常在5-15次迭代中收敛。
最后，回答如下问题

1. 当收敛时 $\theta$的值是多少？
2. 显示牛顿法中 $L$是如何减少的？
3. 画出决策边界
4. 测试1的成绩为20分和测试2为80分的学生不被录取的概率是多少？
5. 对比梯度下降法和牛顿法，你学到了什么？