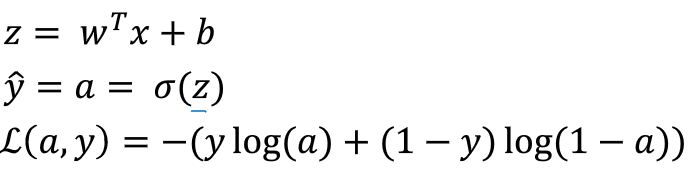1 二分类

m样本数目，n样本特征数目
建议使用的符号表示

$X = \left[\begin{matrix} | & | &&& | \\ ~& ~&&& ~ \\ x^{(1)} & x^{(2)} &\cdots&& x^{(m)} \\ ~& ~&&& ~ \\ | & | &&& | \end{matrix}\right] \in R^{n \times m} \\ ~~\\ ~~ \\ y = \left[\begin{matrix} y^{(1)} & y^{(2)} &\cdots&& y^{(m)} \end{matrix}\right] \in R^{1 \times m}$

2 logistic regression

二分类算法，目的是最小化预测结果和真实结果之间的误差。

给定 $x \in R^n$ ，目的是得到 $\hat{y} = P(y=1|x), 0 \leq \hat y \leq 1$ 。

输入: $x \in R^n$ ；
输出: $y \in \{0,1\}$ ;
参数: $W \in R^n$ ；
偏置: $b \in R$ ；
输出: $\hat y = \sigma(W^Tx+b)$
激活函数：sigmoid， $\sigma(x)=\frac{1}{1+e^{-x}}$
在这里插入图片描述 $z \rightarrow +\infty,\sigma(z) \rightarrow 1$ ;
$z \rightarrow -\infty,\sigma(z) \rightarrow 0$ ;
$z = 0,\sigma(z) = 0.5$ 。

3 logistic regresstion cost function

loss function：在单个样本上定义的损失，衡量的是在单个训练样本上的表现；
cost function：在整个训练集上定义的损失，衡量的是在整个训练集上的表现。

logistic regression loss function:
$L(y^{(i)},\hat{y}^{(i)}) = - (y^{(i)}\log(\hat{y}^{(i)})+(1-\hat{y}^{(i)})\log(1-\hat{y}^{(i)}))$
$~$
$y^{(i)} = 0,L(y^{(i)},\hat{y}^{(i)})=-\log(1-\hat{y}^{(i)})$ ，为了尽可能减小 $L(y^{(i)},\hat{y}^{(i)})$ ，需要 $1-\hat{y}^{(i)}$ 越大越好，也就是需要 $\hat{y}^{(i)}$ 越小越好，而 $\hat{y}^{(i)} \in \{0,1\}$ ，因此，即希望 $\hat{y}^{(i)}$ =0；
$~$
$y^{(i)} = 1,L(y^{(i)},\hat{y}^{(i)})=-\log(\hat{y}^{(i)})$ ，为了尽可能减小 $L(y^{(i)},\hat{y}^{(i)})$ ，需要 $\hat{y}^{(i)}$ 越大越好，而 $\hat{y}^{(i)} \in \{0,1\}$ ，因此，即希望 $\hat{y}^{(i)}$ =1。

训练样本集的cost function：
$J(W,b)=\frac{1}{m}\sum_{i=1}^{m}L(y^{(i)},\hat{y}^{(i)})=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\log(\hat{y}^{(i)})+(1-\hat{y}^{(i)})\log(1-\hat{y}^{(i)})]$
训练logistic regression模型时，目的是找到cost function最小时的W和b。

为什么代价函数是这个样子呢？
对于logistic regression，已知模型给出的是当前样本属于正样本的预测概率；如果当前单个训练样本的ground truth=1，则 $p(y|x)=\hat y$ ；若当前单个训练样本的ground truth=0，则 $p(y|x)=1 - \hat y$ 。对于正样本而言，我们希望模型预测该样本为正样本的概率越大越好，即 $\hat y$ 越大越好；而对于负样本，我们希望模型预测该样本为负样本的概率越大越好，即 $1 - \hat y$ 越大越好，同样是 $\hat y$ 越大越好。因此，把这两种情况合并起来，得到了表达式：
$p(y|x)={\hat y}^y+(1 - \hat y)^{(1 - y)}$
对于上式，若y=1，则 $p(y|x)={\hat y}$ ；若y=0，则 $p(y|x)={1 - \hat y}$ 。和原来的预期结果是一致的。

由于对于m个样本组成的训练集来说，样本之间独立同分布，所以为了求得一组参数使得这一组样本的估计值都尽可能的准确，我们需要使该样本集的联合概率越大越好，即最大化 $\Pi_{i=1}^mp(y^{(i)}|x^{(i)})$ 。而由于log函数为单独递增函数，最大化 $\Pi_{i=1}^mp(y^{(i)}|x^{(i)})$ 和最大化 $\log \Pi_{i=1}^mp(y^{(i)}|x^{(i)})$ 可以得到同样的最优解，但是把乘积运算变成了求和运算，计算更加简单。因此，目的就变成了最大化 $\log \Pi_{i=1}^mp(y^{(i)}|x^{(i)})$ ，也就是极大似然估计。

而对于代价函数来说，我们目的是要最小化它的，因此，这里加一个符号，变成最小化 $-\log \Pi_{i=1}^mp(y^{(i)}|x^{(i)})$ 。而添加一个系数 $\frac{1}{m}$ 纯粹是为了计算方便。

综上，我们最终想要最小化的代价函数为：
$J(W,b)=\frac{1}{m}\sum_{i=1}^{m}L(y^{(i)},\hat{y}^{(i)})=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\log(\hat{y}^{(i)})+(1-\hat{y}^{(i)})\log(1-\hat{y}^{(i)})]$

4 梯度下降

在这里插入图片描述
随机初始化参数，得到一个初始的J(W,b)，在每一点处沿着梯度最大的方向前进，逐步减小J(W,b)的值，下降路径如上图红色箭头所示。最终收敛到全局最优解。

在这里插入图片描述最优解右侧，梯度大于0，减梯度，w向左侧移动；
最优解左侧，梯度小于0，减梯度，w向右侧移动。

更新规则：
repeat
{
w := w - $\alpha~dw$
b := b - $\alpha~db$
}

5 计算图

在这里插入图片描述

6 logistic regression梯度计算

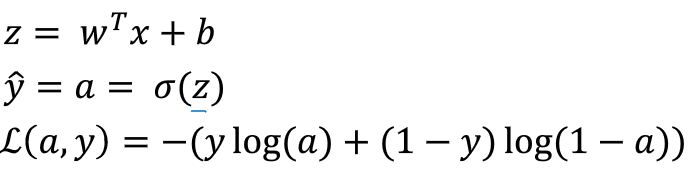
在这里插入图片描述

在这里插入图片描述
基于m个样本进行logistic regression的训练：

初始化：
$J = 0;dW_1=0;dW_2=0;db = 0;$

单次梯度下降更新：
$for ~i = 1~to ~m:$
$~~~~~~~z^{(i)}=W^Tx^{(i)}+b$
$~~~~~~~a^{(i)}=\sigma(z^{(i)})$
$~~~~~~~J += -[y^{(i)}\log(a^{(i)})+(1-y^{(i)})\log(1-a^{(i)})]$
$~~~~~~~dz^{(i)}=a^{(i)} - y^{(i)}$
$~~~~~~~dW_1 += dz^{(i)}x_1$
$~~~~~~~dW_2 += dz^{(i)}x_2$
$~~~~~~~db += dz^{(i)}$
$J /= m$
$dW_1 /= m$
$JW_2 /= m$
$W_1 = W_1 - \alpha~dW_1$
$W_2 = W_2 - \alpha~dW_2$
$b = b - \alpha~db$

两个缺点：一是需要遍历所有的样本(i = 1 … m)，第二是需要遍历所有的特征( $dW_1,dW_2$ )，计算量太大。
解决办法：用向量化代替for循环。

7 向量化

向量化代替第二个for循环：
在这里插入图片描述
向量化替代两个for循环，这里体现了将X表示成列向量形式矩阵的好处：

上图右侧保留的for循环表示进行1000次的梯度下降，该for循环没有办法再通过向量化进行消除。

8 python广播

在这里插入图片描述
python中numpy的reshape操作很高效，可以在计算之前进行reshape保证对正确大小的矩阵进行处理。

在这里插入图片描述
不要用shape为(n,)的秩为1的数组；多使用assert确保变量的shape是正确的；reshape开销很小，可以用来改变变量的排列shape。

9 作业

numpy中，* 和 np.multiply 表示逐元素相乘；np.dot(a,b)表示矩阵乘积；np.outer(a,b)表示向量的外积。

math.exp(x)表示对标量x进行指数运算，其无法对list进行运算；但是，np.exp([1,2,3])的输出为[ $e^1,e^2,e^3$ ]。

计算范数，||x|| = np.linalg.norm(x,ord=2,axis=0,keepdims=True);

训练样本排列时，将每一个样本组成一个列向量。

对于形状为(a,b,c,d)的数组，可以使用
x_flatten = x.reshape((a,-1)).T 将其变换成（bcd,a）的形状。

deeplearning.ai学习笔记：第一课第二周